920
5 Проблеми, які вдарили мозок навіть математикам
3610Р. 4200Р.
Математика є точною наукою, але навіть є проблеми і факти, які вчені називають парадоксами. Щоб зрозуміти і вирішувати їх, потрібно процідити мозок.
Веб-сайт Ось 5 цікавих математичних парадоксів.
English, Українська, Français...
Уявіть, що ви знаходитесь в грі, де ви повинні вибрати один з 3 дверей. За одним дверима є автомобіль, за другий два кози. Ви обираєте одну з дверей, наприклад, номер 1, потім господар, який знає, де знаходиться автомобіль і де кози, відкриває одну з решти дверей, наприклад, номер 3, за якою є козака.
Він запитує вас, якщо ви хочете змінити свій розум і вибрати номер двері 2. Чи будуть Ваші шанси виграти автомобіль, якщо ви приймаєте пропозицію представника та змінити свій вибір?
У цьому задачі необхідно виконати наступні умови:
Нехай це прямо.
Найкраща стратегія виграти цю гру, щоб змінити свій вибір.
Двері 1 Двері 2 Двері 3 Якщо ви не змінюєте своє рішення Якщо ви змінюєте свій розум. Гоат машини козячої машини козячої машини козячої машини козячої машини козячої машини козячої машини
Якщо ви обираєте одну дверцята, то ваші шанси виграти лише 1/3. Зміна розуму і шансів – 2/3.
Звичайно, це тільки працює, якщо ви хочете виграти автомобіль, а не коза.
Fact 2. Ідеальна паралелограма з будь-якого нестандартного малюнка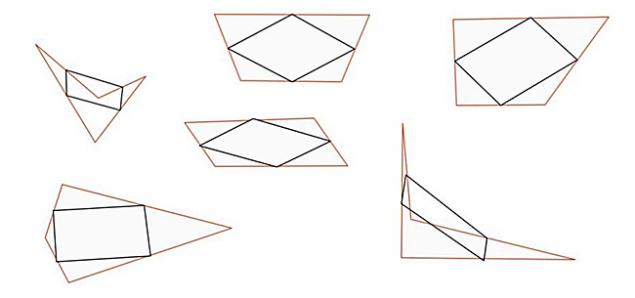
Візьміть папір і намалюйте будь-яку фігуру, яка приходить до розуму. Головне - мати 4 кути і прямі лінії.
Помістіть крапку рівно посередині кожної лінії. При підключенні точок ви отримаєте ідеальний паралелограм.
Fact 3. Парадокс Bertrand (Бертранд)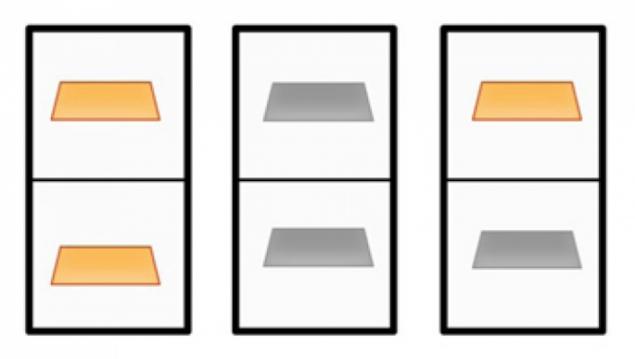
Уявіть, що у вас є 3 коробки з 2 відділеннями. Перший містить 2 золоті бари. У другому, 2 срібні бруски. У третьому лежанні золоті і срібні бруски.
Вибираємо будь-яку коробку і відкрийте одну з відділень. Якщо є золотий бар, що є ймовірність того, що в іншому відсіку буде однаковий бар?
Ви думаєте, що коефіцієнти 1/2?
Так як у нас є лише 2 коробки золотих барів, і ви, ймовірно, взяли одне з них. Тим не менш, шанси вгадати менше, ніж ви думаєте.
Це насправді набагато складніше. Для того, щоб дізнатися, що відбувається, дайте позначку коробки.
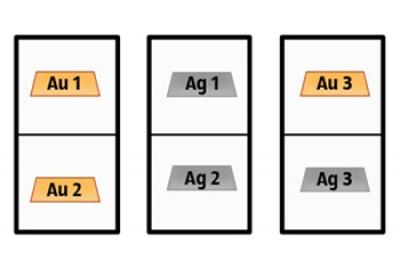
Далі проводимо всі можливі комбінації розташування заготів у ящиках. Зробіть акцент на тих, хто має золоті бари.
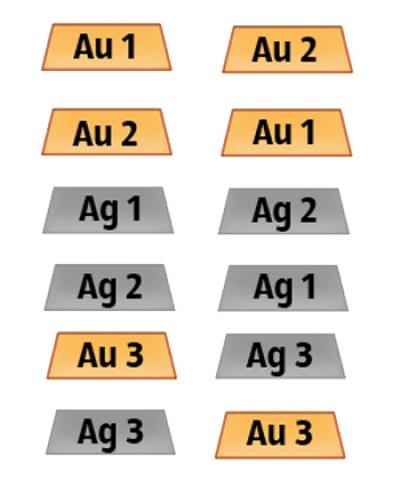
Таким чином, на основі математичних обчислень, виходить, що шанси вгадати правильний ящик 1/3.
Факт 4. 0.999 = 1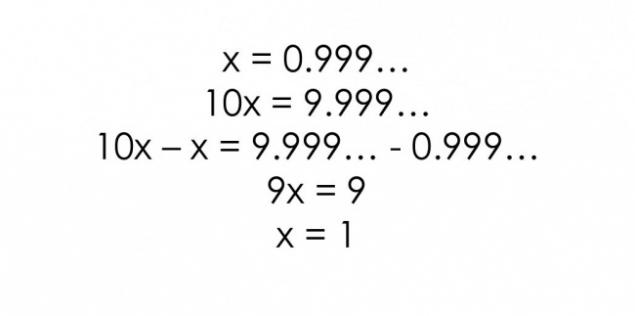
Рекорд 9 в десятковій дробі дає 1.
Є деякі докази, що це правда, але багато людей все ще намагаються зрозуміти його.
Одна з причин, чому люди не вірять це, тому що ми важко прийняти факт нескінченності. Здається, що десь має бути останній 9.
Номери можуть відрізнятися, але не є винятком.
Причиною є наше розуміння нескінченності.
І ми також представимо ще один доказ, якщо перший не зданий переконливо.
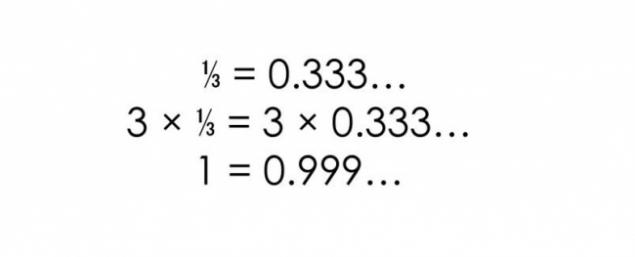
Fact 5. Нескінченні набори натуральних чисел, як і навіть:
Ми можемо переготовити натуральні і навіть номери, таким чином, що для кожного натурального числа є навіть число.
Подумайте про це. Кожен натуральний номер має ще один номер, який двічі його розмір, і кожен навіть номер має природну кількість, за якою він розділений навпіл.
Що означає?
Дивитися також:
Не чарівний. Це фізика.
35 Безкоштовні сайти навчання
Веб-сайт: www.businessinsider.com
Математика є точною наукою, але навіть є проблеми і факти, які вчені називають парадоксами. Щоб зрозуміти і вирішувати їх, потрібно процідити мозок.
Веб-сайт Ось 5 цікавих математичних парадоксів.
English, Українська, Français...
Уявіть, що ви знаходитесь в грі, де ви повинні вибрати один з 3 дверей. За одним дверима є автомобіль, за другий два кози. Ви обираєте одну з дверей, наприклад, номер 1, потім господар, який знає, де знаходиться автомобіль і де кози, відкриває одну з решти дверей, наприклад, номер 3, за якою є козака.
Він запитує вас, якщо ви хочете змінити свій розум і вибрати номер двері 2. Чи будуть Ваші шанси виграти автомобіль, якщо ви приймаєте пропозицію представника та змінити свій вибір?
У цьому задачі необхідно виконати наступні умови:
- Автомобіль розміщується за будь-яким з 3-х дверей.
- У будь-якому випадку хост зобов'язаний відкрити двері з козаком (але не обрано одного гравця) і запросити гравця змінити свій вибір.
- Якщо у хостелі є вибір, як до якого з двох дверей для відкриття, він вибирає або з однаковою ймовірністю.
Нехай це прямо.
Найкраща стратегія виграти цю гру, щоб змінити свій вибір.
- Якщо гравець вибирає різні двері, він може втратити тільки, якщо був автомобіль за дверима, він вирішив відкрити спочатку і не змінив його розуму.
- Оскільки ймовірність вибору правих дверей становить 1/3, шанси втратити гру, коли ви зміните свій вибір також 1/3.
- Це означає, що людина з подібною стратегією перемагає в двох випадках трьох, ніж хтось, хто завжди зупиняється на одній двері.
Двері 1 Двері 2 Двері 3 Якщо ви не змінюєте своє рішення Якщо ви змінюєте свій розум. Гоат машини козячої машини козячої машини козячої машини козячої машини козячої машини козячої машини
Якщо ви обираєте одну дверцята, то ваші шанси виграти лише 1/3. Зміна розуму і шансів – 2/3.
Звичайно, це тільки працює, якщо ви хочете виграти автомобіль, а не коза.
Fact 2. Ідеальна паралелограма з будь-якого нестандартного малюнка

Візьміть папір і намалюйте будь-яку фігуру, яка приходить до розуму. Головне - мати 4 кути і прямі лінії.
Помістіть крапку рівно посередині кожної лінії. При підключенні точок ви отримаєте ідеальний паралелограм.
Fact 3. Парадокс Bertrand (Бертранд)

Уявіть, що у вас є 3 коробки з 2 відділеннями. Перший містить 2 золоті бари. У другому, 2 срібні бруски. У третьому лежанні золоті і срібні бруски.
Вибираємо будь-яку коробку і відкрийте одну з відділень. Якщо є золотий бар, що є ймовірність того, що в іншому відсіку буде однаковий бар?
Ви думаєте, що коефіцієнти 1/2?
Так як у нас є лише 2 коробки золотих барів, і ви, ймовірно, взяли одне з них. Тим не менш, шанси вгадати менше, ніж ви думаєте.
Це насправді набагато складніше. Для того, щоб дізнатися, що відбувається, дайте позначку коробки.

Далі проводимо всі можливі комбінації розташування заготів у ящиках. Зробіть акцент на тих, хто має золоті бари.

Таким чином, на основі математичних обчислень, виходить, що шанси вгадати правильний ящик 1/3.
Факт 4. 0.999 = 1
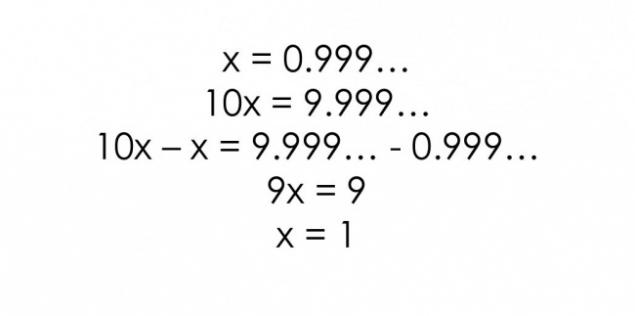
Рекорд 9 в десятковій дробі дає 1.
Є деякі докази, що це правда, але багато людей все ще намагаються зрозуміти його.
Одна з причин, чому люди не вірять це, тому що ми важко прийняти факт нескінченності. Здається, що десь має бути останній 9.
Номери можуть відрізнятися, але не є винятком.
Причиною є наше розуміння нескінченності.
І ми також представимо ще один доказ, якщо перший не зданий переконливо.
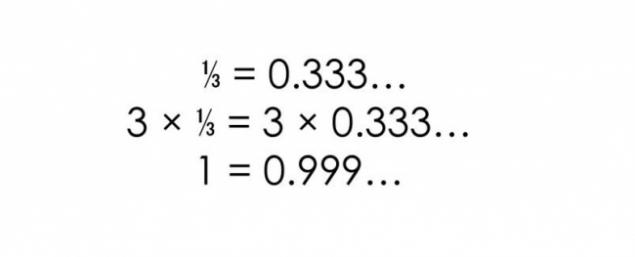
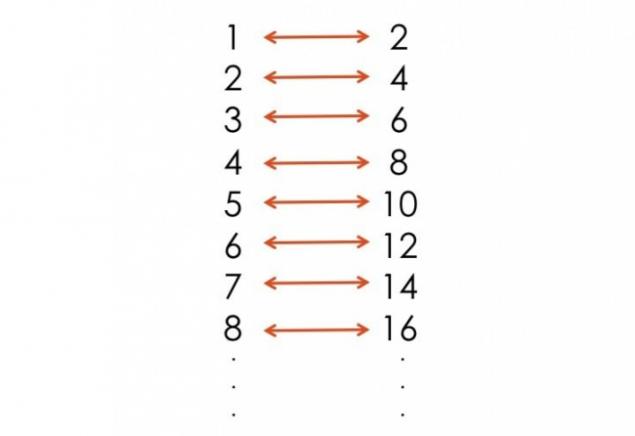
Fact 5. Нескінченні набори натуральних чисел, як і навіть:
- Природні номери 1, 2, 3 та ін.
- Є нескінченна кількість природних чисел.
- Також є нескінченна кількість парних чисел.
Ми можемо переготовити натуральні і навіть номери, таким чином, що для кожного натурального числа є навіть число.

Подумайте про це. Кожен натуральний номер має ще один номер, який двічі його розмір, і кожен навіть номер має природну кількість, за якою він розділений навпіл.
Що означає?
- Кожен натуральний номер також відповідає навіть номеру.
- Ви також можете віднести реальні номери до одного.
Дивитися також:
Не чарівний. Це фізика.
35 Безкоштовні сайти навчання
Веб-сайт: www.businessinsider.com