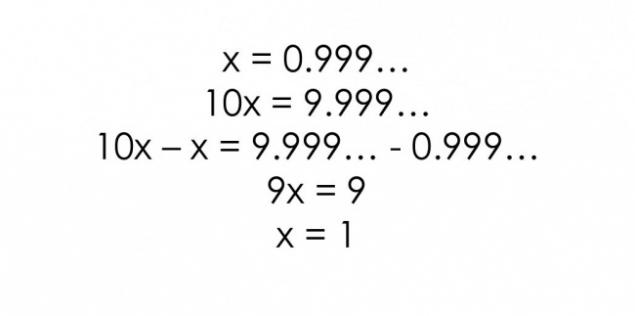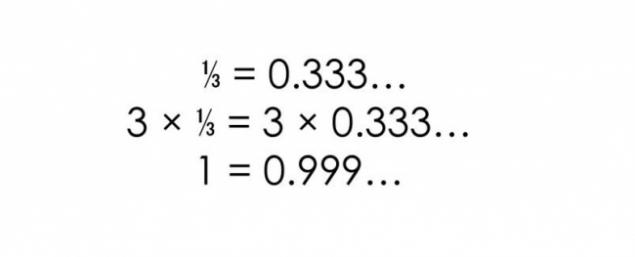5脑筋急转弯，即使数学家疯狂

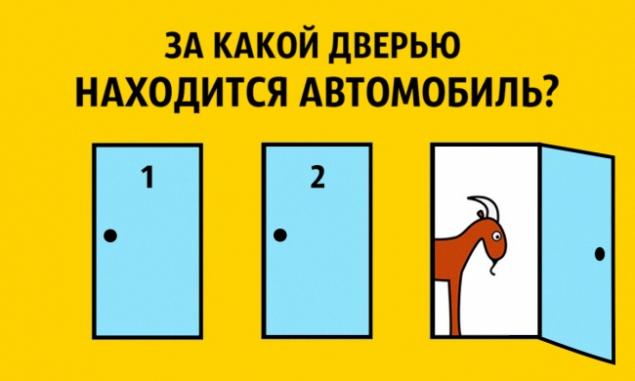
数学 - 确切的科学，但即使在那里也有困惑和事实，科学家称之为悖论。为了理解和解决的需要，以应变的大脑。

网站 STRONG>我已经为您选择5有趣的数学悖论。

情况1.蒙特门的难题 H3>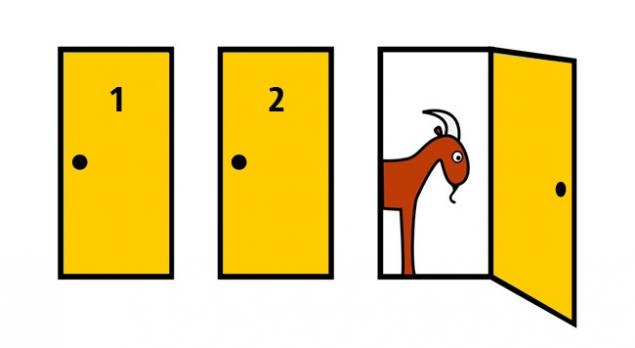



想象一下，你参与了游戏中，你必须选择的三个门之一。一个门后面是一个汽车其他两个 - 山羊。您可以选择其中一个门，例如，1号，那么领导者，谁知道车子，哪里 - 山羊，打开剩下的一扇门，例如，3号，这是一个山羊
。
然后，他会询问您是否要更改选择，然后选择门№2 会增加你的机会赢得一辆车，如果接受要约的铅和改变你的选择？ STRONG>

在此任务中，必须符合以下条件：

在这款车同样可能发布的任何三个门。 铅不得不打开与山羊的门（而不是一个由玩家选择），并提供玩家更改选择的任何情况。 如果主机有一个选择，把两个柜门打开这，他选择的任何人以相同的概率。 如果你坚持选择，你可能会失去。这是为什么呢？毕竟，机会来猜车为50/50。 STRONG>

让我们来处理：

以赢得比赛的最佳策略 - 是要改变你的选择 STRONG>
。
如果一个球员选择一个不同的门，他可能会失去只有在门口，他决定开原，并没有改变他的意见，是汽车。 由于权选择权的概率门 - 1/3，输掉比赛的话，当你改变你的选择，也等于1/3的几率 这意味着，一个人打赢两场三种情况中的一个类似的策略，不是一个谁。总是停在门口的一个。 还是不相信？再看看它包含了所有可能的事件表。 STRONG>

门1号 STRONG> 门2号 STRONG> 门3号 STRONG> 的结果，如果不改变他的决定 STRONG> 的结果，如果改变决定 STRONG>机机器山羊山羊山羊山羊山羊山羊机机机山羊山羊山羊机



如果你停止你的选择上一扇门，你获胜的机会只有1/3。有必要改变你的想法 - 和赔率是2/3
。
所有工作的，当然，前提是你要赢了车，而不是山羊。 STRONG>

事实2.任何非标准形状完美的平行四边形 H3>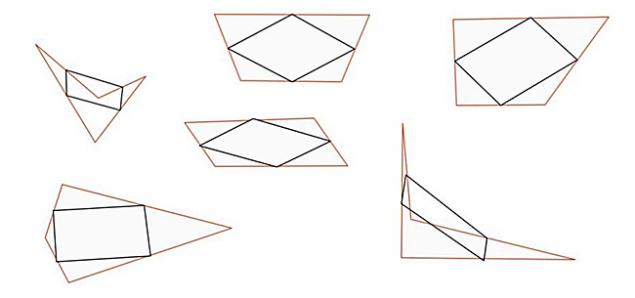



拿一张纸，并绘制想到的任何形状。 最主要的是有4个弯道和直线。 STRONG>

放点恰好在各行的中间。连接点，你会得到一个完美的平行四边形。

事实3.箱贝特朗（伯川德悖论）悖论 H3>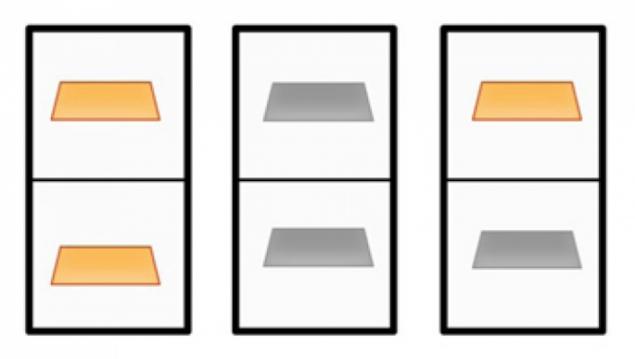



试想一下，你有3盒，2车厢。第2是金元宝。在第二个 - 2银元宝。第三个谎言黄金和银条。

您可以选择任何框，打开分支机构。 如果有一根金条，是什么，在其他车厢是一样的吧概率是多少？ STRONG>

当然，你，认为赔率是1/2？

因为我们只有2盒，金条内，你可能有其中之一。然而，猜测不到你认为的机会。

这真是要复杂得多。要了解它是什么，让我们表示框。





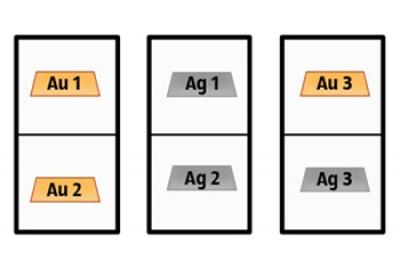
然后zarisuem的位置吧所有可能的组合在盒子里。我们专注于那些有金条。





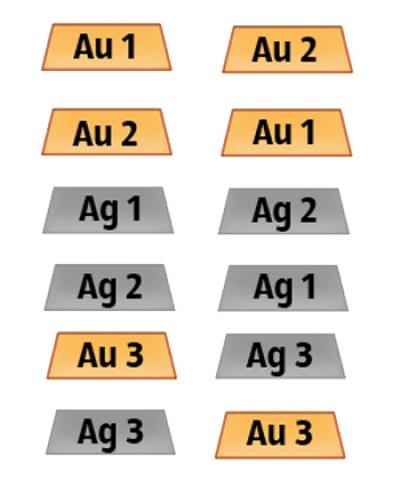
因此，数学计算的基础上，事实证明，猜测正确的盒子等于1/3的机会。

事实4. 0，999 = 1 H3>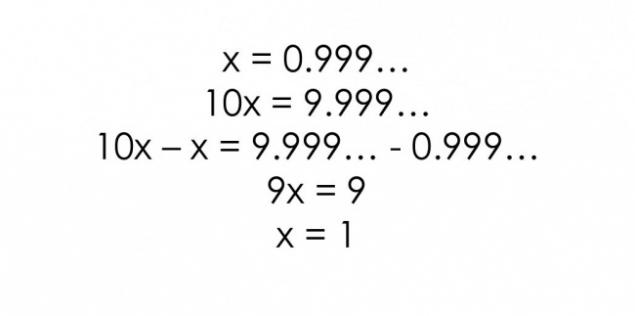





重复9十进制给出1 STRONG>

有一些证据表明，这是真实的，但很多人仍试图反驳他们。

其中一个原因，为什么人们不相信这种说法，是我们难以接受无穷的事实。似乎冥冥中有必须在最后的数字9

这些数字可能会有所不同，但没有异常。

原因只有在我们无限的理解。

并提出其他证据，如果第一次你似乎没有足够的说服力。

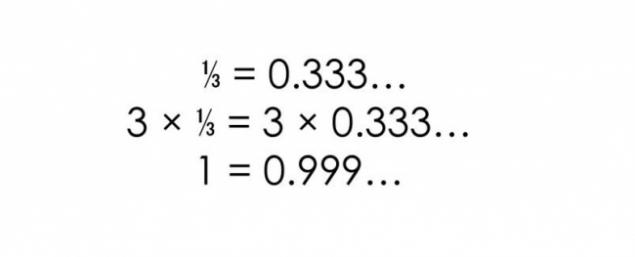
事实5.无限集合 H3>自然数一样多，甚至：

的自然数。 - 。1，2，3，等对D 还有自然数的无限数量 还有偶数无限数量 您可能会认为自然数甚至超过。而这将是一个错觉。 STRONG>

我们所涉及的自然数，甚至，由此证明，对于每一个自然数是偶数。





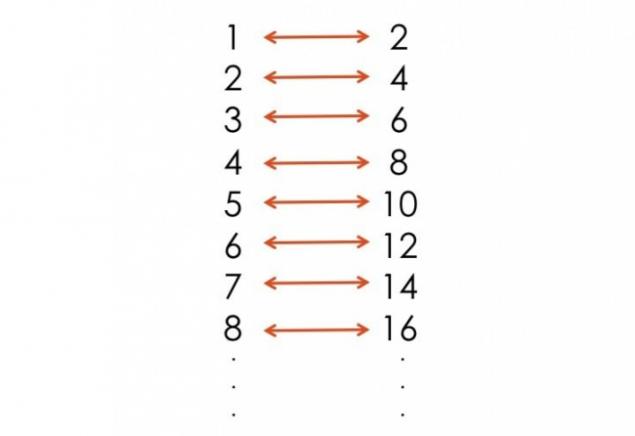
想想吧。每一个正整数都有不同数目的两倍他的大小，和每个偶数是正整数作其分为两半。

它的意思： STRONG>

在每个自然数也符合并偶数。 您将无法相互关联的整数和实数。





参见： STRONG>
这不是魔术。这 - 物理
35免费培训网站

通过<一href="http://www.businessinsider.com/the-most-controversial-math-problems-2013-3?utm_content=bufferd2f20&utm_medium=social&utm_source=facebook.com&utm_campaign=buffer">www.businessinsider.com/the-most-controversial-math-problems-2013-3?utm_content=bufferd2f20&utm_medium=social&utm_source=facebook.com&utm_campaign=buffer