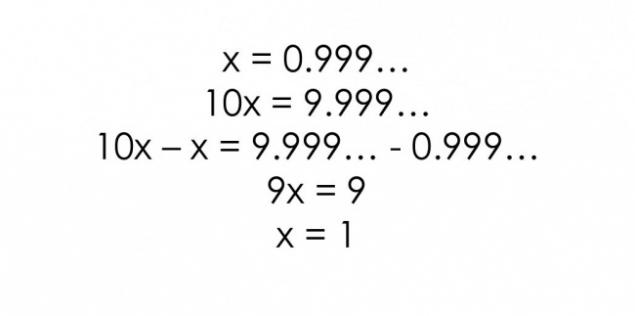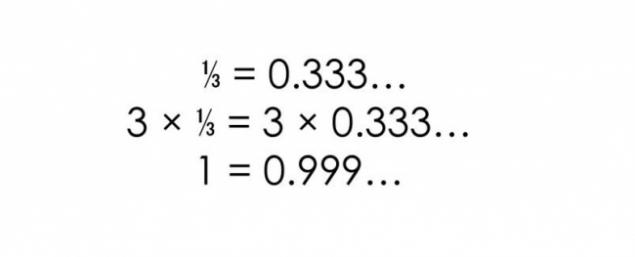920
5 rompecabezas que incluso matemáticos locos
Matemáticas - una ciencia exacta, pero incluso allí hay rompecabezas y hechos, que los científicos llaman paradojas. Con el fin de comprender y resolver la necesidad de forzar el cerebro.
< Sitio web que he seleccionado para usted 5 paradojas matemáticas interesantes.
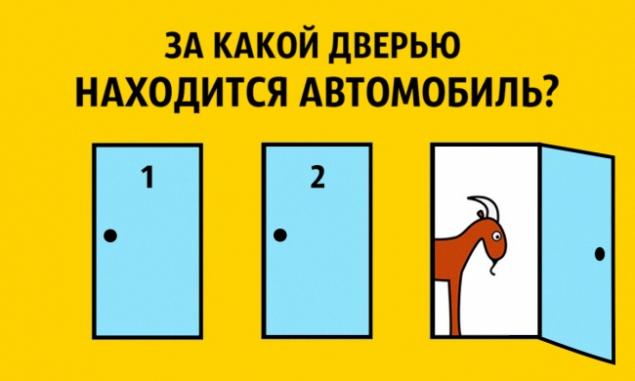
Hechos 1. El problema de Monty Hall h3> 
Imagínese que usted está involucrado en un juego en el que tienes que elegir una de las tres puertas. Detrás de una puerta es un coche para los otros dos - una cabra. Solo tiene que elegir una de las puertas, por ejemplo, el número 1, entonces el líder, quién sabe dónde está el coche, y donde - cabras, se abre una de las puertas restantes, por ejemplo, el número 3, que es una cabra
.
Luego le pregunta si desea cambiar su selección y elija la puerta № 2. ¿Aumenta tus posibilidades de ganar un coche, si acepta una oferta la iniciativa y cambiar su selección?
En esta tarea, con sujeción a las siguientes condiciones:
El coche es igualmente probable publicado por cualquiera de las tres puertas. El plomo, en todo caso obligado a abrir una puerta con una cabra (pero no el elegido por el jugador), y ofrecer al jugador para cambiar la selección. Si el host tiene una opción, ¿cuál de las dos puertas abiertas, elige cualquiera de ellos con la misma probabilidad. Si usted insiste en la elección, es probable que perder. ¿Por qué es eso? Después de todo, las posibilidades de adivinar el coche era de 50/50. Vamos trato:
La mejor estrategia para ganar el juego - es cambiar su elección
.
Si un jugador selecciona una puerta diferente, que puede perder si la puerta, se decidió abrir el original y no ha cambiado de opinión, fue el coche. Desde la probabilidad de derecho a elegir la derecha puerta - 1/3, entonces la posibilidad de perder el juego cuando usted cambia su selección, también igual a 1/3 Esto significa que una persona con una estrategia similar de ganar dos de los tres casos, que el que. siempre se detiene en una de las puertas. Todavía no creen? Entonces eche un vistazo a la tabla que contiene todos los eventos posibles.
número de puerta 1 La puerta número 2 La puerta número 3 El resultado, si no cambia su decisión El resultado, si cambiar su decisión de cabra Máquina de cabra cabra cabra cabra cabra Máquina Máquina de cabra cabra máquina cabra
Si deja de su elección en una de las puertas, las probabilidades de ganar son sólo 1/3. Es necesario cambiar de opinión - y las probabilidades son 2/3
.
Todo esto funciona, por supuesto, sólo si quieres ganar el coche, no la cabra.
Hecho 2. El paralelogramo perfecta de cualquier forma no estándar h3> 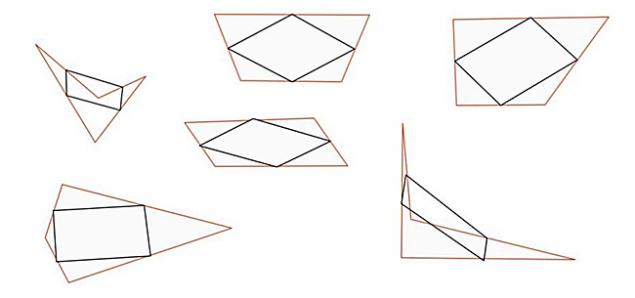
Tome una hoja de papel y dibujar cualquier forma que viene a la mente. Lo principal es tener 4 esquinas y líneas rectas.
Coloque el punto exactamente en el centro de cada línea. Une los puntos, obtendrá un paralelogramo perfecto.
Hecho 3. La paradoja de la caja Bertrand (Bertrand Paradox) h3> 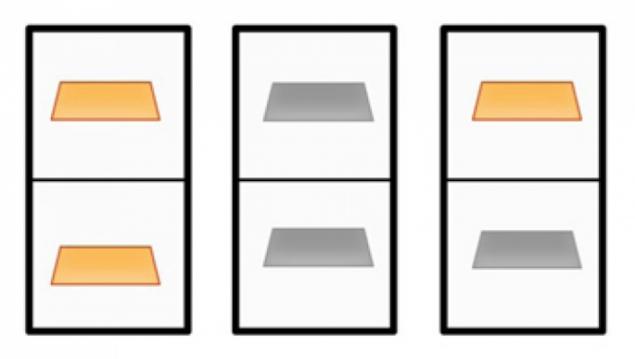
Imagina que tienes 3 cajas con 2 compartimentos. Los 2 primeros son lingotes de oro. En el segundo - lingote de plata 2. El tercer oro mentira y lingotes de plata.
Usted selecciona cualquier caja y abre una de las oficinas. Si hay una barra de oro, ¿cuál es la probabilidad de que en el otro compartimiento es el mismo bar?
Usted, por supuesto, piensa que las probabilidades están en medio?
Ya que sólo tienen 2 cajas con barras de oro en el interior y es probable que tenga una de ellas. Sin embargo, la posibilidad de adivinar menos de lo que piensas.
Es realmente mucho más complicado. Para saber lo que es, vamos a denotar la caja.
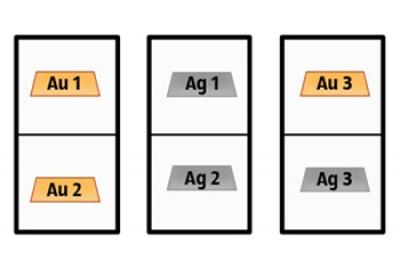
Entonces zarisuem todas las posibles combinaciones de barras ubicación en cajas. Nos centramos en aquellos en los que hay lingotes de oro.
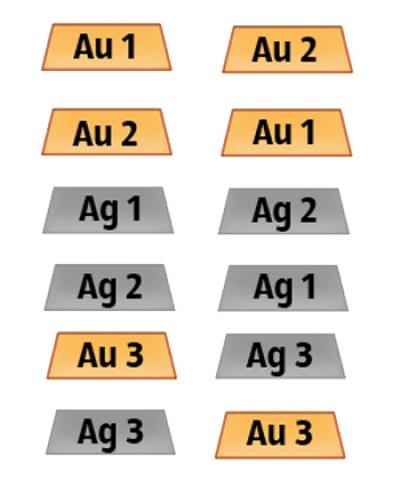
Por lo tanto, sobre la base de cálculos matemáticos, resulta que las posibilidades de adivinar la casilla correcta igual a 1/3.
Hecho 4. 0, 999 = 1 h3> 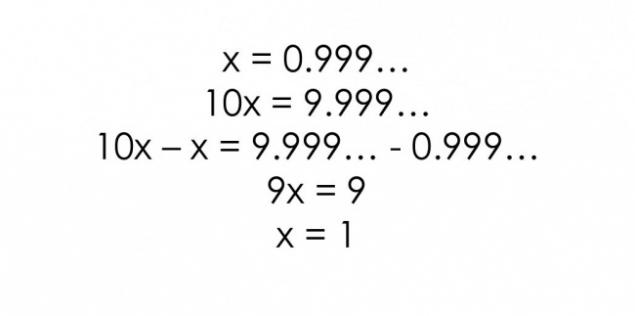
La repetición 9 decimal da 1.
Existe alguna evidencia de que esto es cierto, pero muchas personas todavía están tratando de refutarlos.
Una de las razones por las cuales las personas no creen en esta declaración, es tan difícil para nosotros aceptar el hecho de infinito. Parece que en algún lugar tiene que ser el último en el número 9.
Los números pueden ser diferentes, pero no hay excepciones.
Razón sólo en nuestra comprensión del infinito.
Y a presentar otras pruebas, si el primero no parecías lo suficientemente convincente.
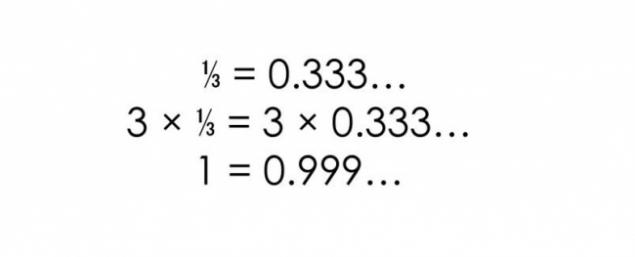
Hecho 5. conjuntos infinitos h3> números naturales tanto como y hasta:
Los números naturales -.... 1, 2, 3, y así sucesivamente d Hay un número infinito de números naturales También hay un número infinito de números pares Usted puede pensar que los números naturales más aun. Y sería un engaño. Podemos relacionar los números naturales, e incluso, lo que demuestra que por cada número natural es un número par.
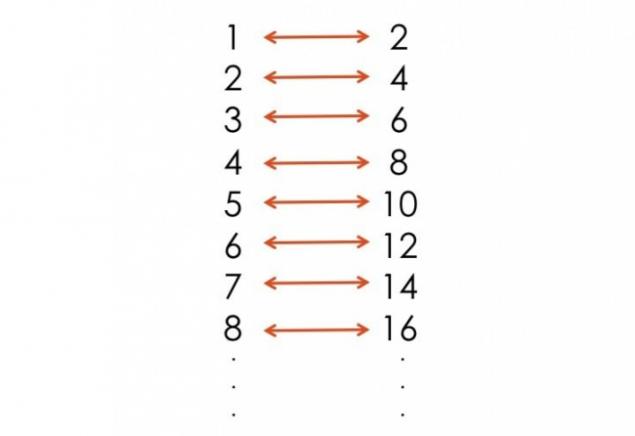
Piense en ello. Cada número entero positivo tiene un número diferente que es dos veces el tamaño de su, y todo número par es un entero positivo para los que se divide por la mitad.
Lo que significa:
Cada número natural también es consistente con y un número par. Usted no será capaz de relacionar entre sí los números enteros y números reales.
Ver también:
No es magia. Es -
física 35 sitios de formación gratuitos
a través de www.businessinsider.com/the-most-controversial-math-problems-2013-3?utm_content=bufferd2f20&utm_medium=social&utm_source=facebook.com&utm_campaign=buffer
10 puzzles de lógica, en la que se encuentra el retén
El complejo está a ejercicios eficaces a la prensa: