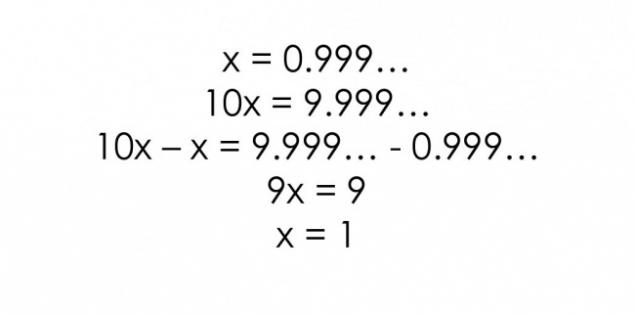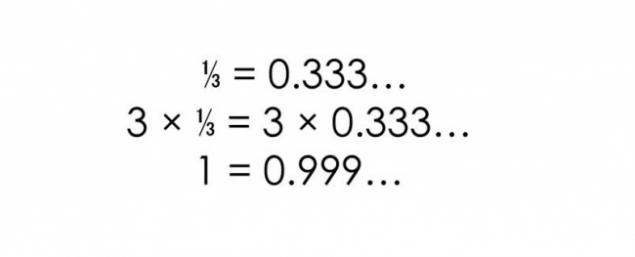920
5 brainteasers that even mathematicians Crazy
Mathematics - an exact science, but even there there are puzzles and facts, which scientists call paradoxes. In order to understand and solve the need to strain the brain.
< Website I have selected for you 5 interesting mathematical paradoxes.
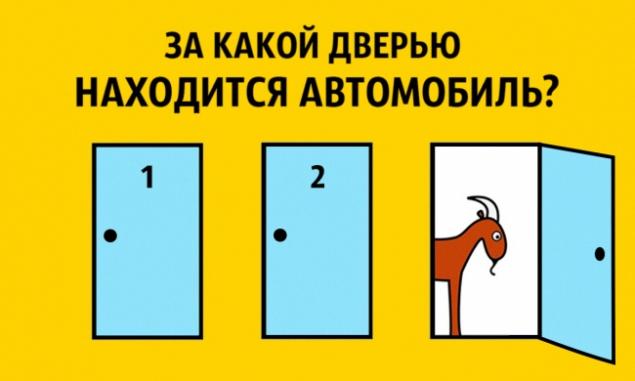
Fact 1. The Monty Hall Problem h3> 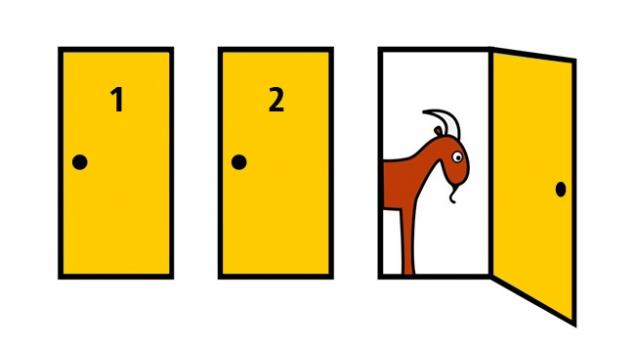
Imagine that you are involved in a game in which you have to choose one of three doors. Behind one door is a car for the other two - a goat. You choose one of the doors, for example, number 1, then the leader, who knows where the car is, and where - goats, opens one of the remaining doors, for example, number 3, which is a goat.
He then asks you whether you wish to change your selection and choose the door № 2. Does increase your chances to win a car, if you accept an offer the lead and change your selection?
In this task, subject to the following conditions:
The car is equally probable posted for any of the three doors. Lead in any case obliged to open a door with a goat (but not the one chosen by the player), and offer the player to change the selection. If the host has a choice, which of the two doors open, he chooses any of them with the same probability. If you insist on choosing, you are likely to lose. Why? After all, the chances to guess the car was 50/50. Let's deal:
The best strategy to win the game - is to change your choice.
If a player selects a different door, he can lose only if the door, he decided to open the original and has not changed his opinion, was the car. Since the probability of right to choose the right door - 1/3, then the chance of losing the game when you change your selection, also equal to 1/3. This means that a person with a similar strategy of winning two of the three cases, than the one who always stops at one of the doors. Still do not believe? Then take a look at the table it contains all possible events.
Door number 1 The door number 2 The door number 3 The result, if not change his decision The result, if change its decision Machine Machine goat goat goat goat goat goat Machine Machine Machine goat goat goat machine
If you stop your choice on one of the doors, your chances of winning are only 1/3. It is necessary to change your mind - and the odds are 2/3.
All this works, of course, only if you want to win the car, not the goat.
Fact 2. The perfect parallelogram of any non-standard shapes h3> 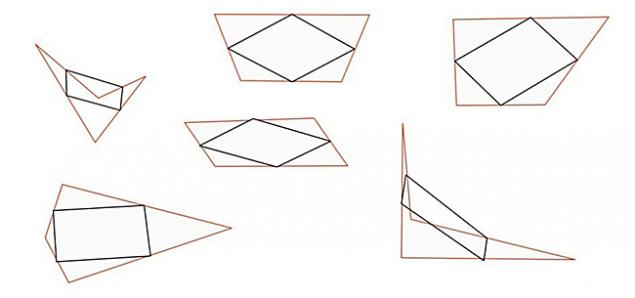
Take a sheet of paper and draw any shape that comes to mind. The main thing is to have 4 corners and straight lines.
Put the point exactly in the middle of each line. Connect the dots, you will get a perfect parallelogram.
Fact 3. The paradox of the box Bertrand (Bertrand Paradox) h3> 
Imagine that you have 3 boxes with 2 compartments. The first 2 are gold ingot. In the second - 2 silver ingot. The third lie gold and silver bullion.
You select any box and open one of the offices. If there is a gold bar, what is the probability that in the other compartment is the same bar?
You, of course, think that the odds are 1/2?
Since we only have 2 boxes with gold bars inside and you probably have one of them. However, the chance of guessing less than you think.
It's really much more complicated. To find out what it is, let us denote the box.
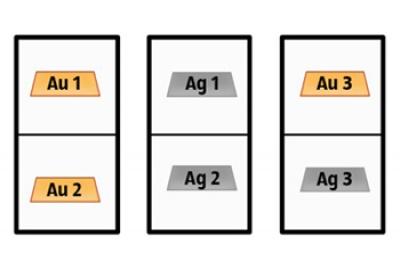
Then zarisuem all possible combinations of location bars in boxes. We focus on those where there is gold bullion.
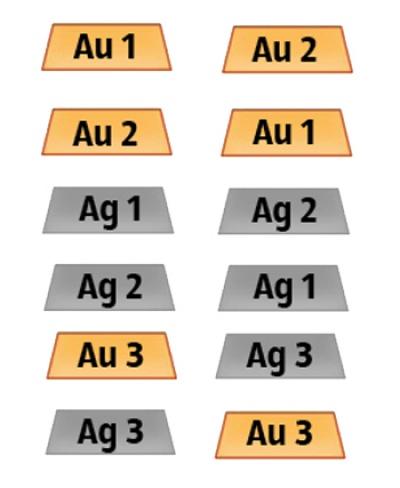
Thus, on the basis of mathematical calculations, it turns out that the chances of guessing the correct box equal to 1/3.
Fact 4. 0, 999 = 1 h3> 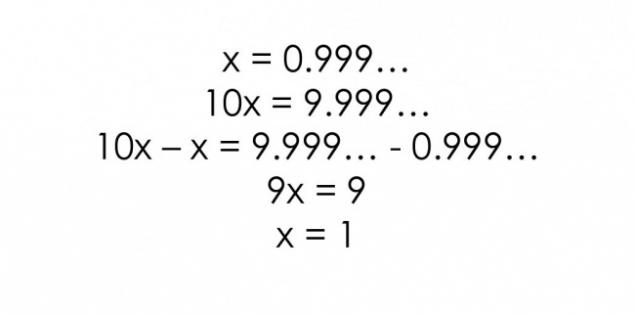
Repetition 9 decimal gives 1.
There is some evidence that this is true, but many people are still trying to refute them.
One of the reasons why people do not believe in this statement, is that difficult for us to accept the fact of infinity. It seems that somewhere there must be the very last in the number 9.
The numbers may be different, but there are no exceptions.
Reason only in our understanding of infinity.
And to present other evidence, if the first you seemed not convincing enough.
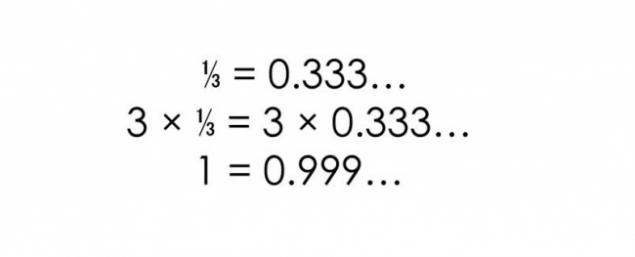
Fact 5. Infinite sets h3> natural numbers as much as and even:
The natural numbers - 1, 2, 3, and so on. d. There are an infinite number of natural numbers. There is also an infinite number of even numbers. You may think that the natural numbers more than even. And it would be a delusion. We can relate the natural numbers and even, thus proving that for every natural number is an even number.
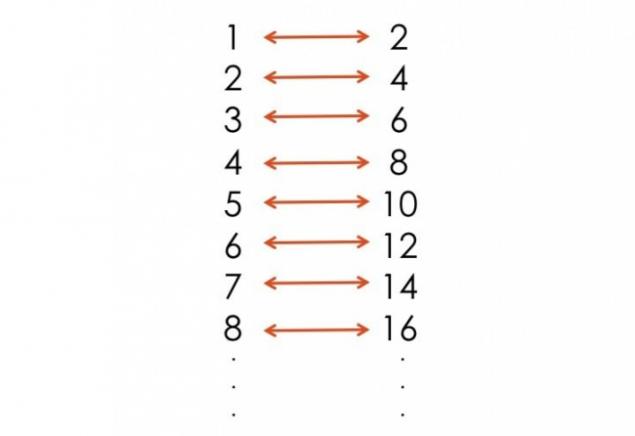
Think about it. Every positive integer has a different number that is twice the size of his, and every even number is a positive integer for which it is divided in half.
What it means:
Each natural number is also consistent with and an even number. You will not be able to relate to each other integers and real numbers.
See also:
It's not magic. It - physics
35 free training sites
via www.businessinsider.com/the-most-controversial-math-problems-2013-3?utm_content=bufferd2f20&utm_medium=social&utm_source=facebook.com&utm_campaign=buffer