589
Just about the complex: why everything tends to chaos and how to stop it
Sometimes when You feel the rising level of entropy, but I don't know why, the answer lies in physics: the desire of the world to chaos is a fundamental property of nature. What is a chaos, let's do it, can it be somehow measured, and why there is the expression "to break — not to build"? All this was explained to a science journalist, an employee of the Department of physics and astrophysics MIPT Hayk Hakobyan.
What happens when we set in motion a pendulum? He begins to waver, each time decreasing amplitude. After a while we discover that the pendulum has stopped. But where did the energy of the pendulum? Those in the high school physics classes listened to the teacher attentively, answer, that energy will take away the air molecules. But why not the reverse? Why do molecules suddenly can't get together and, conversely, transmit energy to the pendulum?
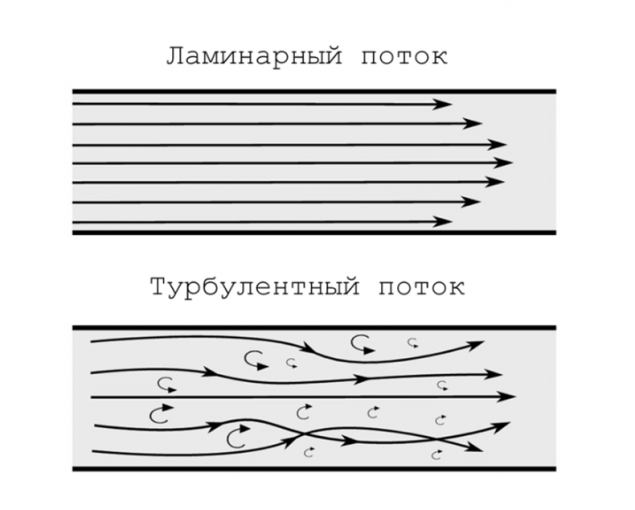
The fact that the desire of the world to chaos is a fundamental property of nature. The directed movement of particles of the pendulum is converted into random motion of air molecules. Directed the flow of water sooner or later turn into a chaotic jet with turbulent eddies and meandering, interwoven with each other flows.
Our nature seeks vengeance to chaos, but is it really the desire of the infinite? At some point the system reaches some kind of peace? At what point is the desire stop? In the nineteenth century, Maxwell and a number of other physicists have shown that if you leave the system alone, it really comes to a certain state of "peace". This condition is called equilibrium, and in order to understand it, you need to forget about the individual rates, the coordinate of each particle and take a look at some collective characteristics of the system. For example, the number of particles at the moment have a certain speed.
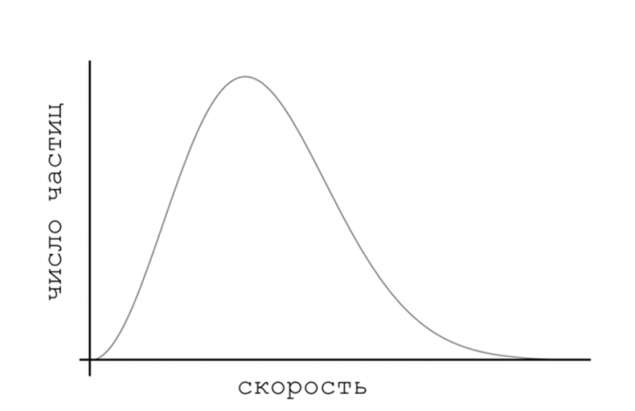
If we plot the number of particles with velocity, we see an amazing thing: the system from any state, whatever this state was initially, in the end comes to one specific distribution of the number of particles with velocity, which is called the Maxwell distribution. This state is the ultimate destination of any system, and it achieves maximum chaos.
But... How do we measure chaos? In physics for measuring chaos using the value called the entropy of the system. The more entropy, the less ordered system. In equilibrium the entropy is maximum. Boltzmann in the XIX century was proved the so-called H-theorem, which States that in a closed system entropy over time always increases.
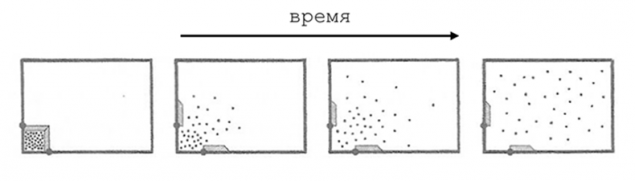
In practice, this is a quite clear of the consequences. If we, for example, take a balloon with helium and blow it into the corner of the room, the gas after some time will spread throughout the room, evenly filling the entire area. Thus, the entropy of the gas will increase and... Yes, in General, that's all. No matter how long we waited, helium will never going back to the pile in the corner of the room. That is, the processes in our world are irreversible: from the goal state we can not know the initial as the final state is the same for all initial States. This is understandable, our experience is quite corresponds. It is always easier to break something than to build, easier to scatter than to gather together. It's all quite logical, right?
Not really. Imagine that you have a closed room with a bunch of balls that fly and bump into each other. Everything is absolutely perfect, elastic collision, no energy loss. After a sufficient amount of time, the velocity distribution is exactly the Maxwell, entropy irreversibly increases to the maximum.
The data of the Planck telescope revealed that approximately 98% of the energy of our Universe is not concluded in the stars and in the ordinary matter, from which we But let's look at each bulb individually. The fact that for each ball we can know exactly its speed and coordinate, but also acting on it force. From Newton's second law can know the acceleration and the motion of each individual particles can clearly ask. Newton's law is time-reversible, as if to turn back time, its form does not amend the law. This means that the movement of each individual ball is also reversible: the final state of the ball can understand where he came from and how to move, but... the movement of all the balls together is irreversible.
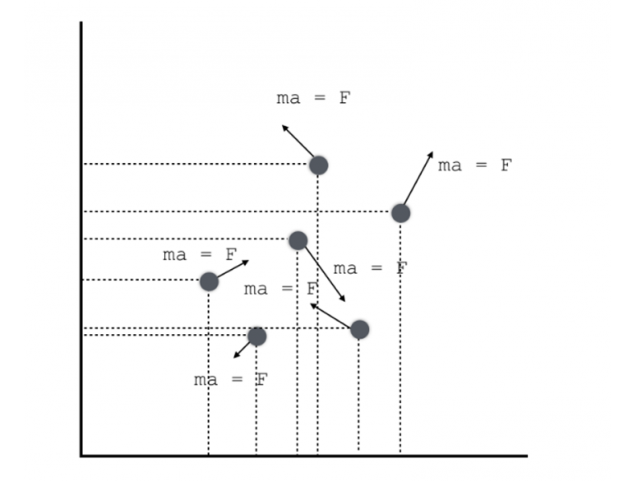
That is the basis of our world are irreversible is quite a reversible laws. This is very strange. What if no irreversibility there, and it's just an illusion? What if the movement is just so complicated that it seems chaotic, but actually it quite regularly?
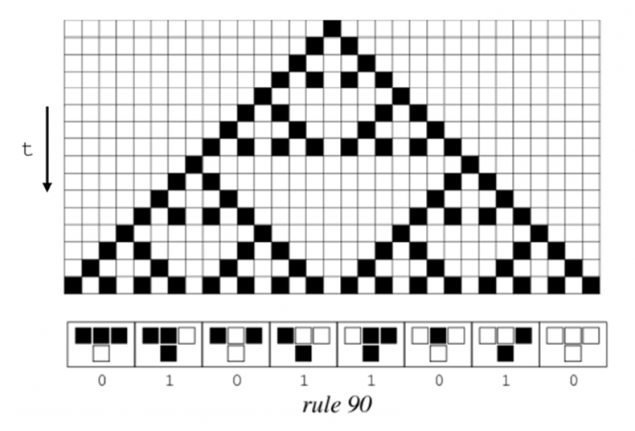
For an example of what I mean, let's take a very interesting system. It's called a cellular automaton. Imagine your universe is a simple series of white and black squares. You — the God of this Universe, and you need to lay down some rule of evolution at the time. And you are laying a very simple rule: if the cell itself is black and the neighboring two cells is also black, in the next step, the cell will be white (pictured bottom left), if the cell is black, its left neighbor is also black, and the neighbor on the right is white, then in the next step the cell will become black and so on. Thus it is possible to set a universal rule (the physics of your Universe. To record the act using zeros and ones or, if we translate them into a decimal record using just one number. In this case (in the picture) this is the rule 90. The evolution of this cellular automaton are shown below.
Such rules exist very much. There are rules, which are based on the previous two steps instead of one or multiple neighbors. There are rules for two-dimensional cellular automaton, where we have now not a number of black and white cells, and a plane.
With the help of cellular automata is already getting quite complex, unpredictable shape — they are used in architecture and game design to build a realistic landscape. But, surprisingly, all this diversity, these unpredictable shapes and figures are defined only by a rule from one number, everything else is a matter of time.
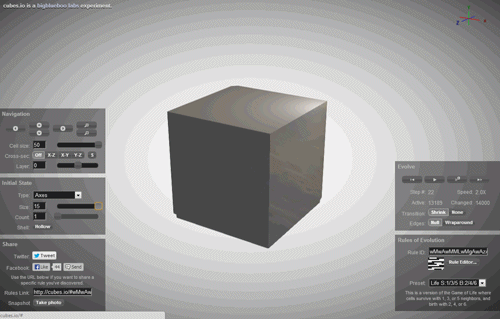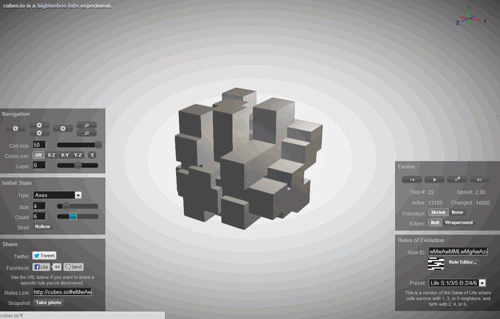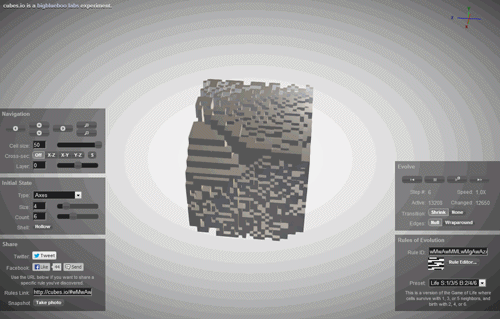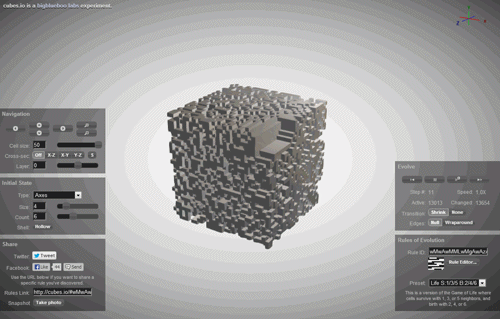
But what if the diversity of our world, all the complex images created by our nature and all the chaos towards which our world is merely the implementation of a cellular automaton? What if we are merely a simulation of a cellular automaton in someone's computer?
As we learned in the first part, at the deepest core of our world are completely reversible laws, where at the end you can restore the initial one. Therefore, if the world is a cellular automaton, it must also be reversible. Such cellular automata really is, but they have one problem. Any reversible cellular automaton has a cycle: after a certain number of steps, the universe is recreated in its original form again, then again and so moves in a cycle.
In our world, unfortunately, this is not... Or is there? French mathematician Henri Poincare for certain types of systems noticed an interesting thing: as a result of the evolution of these systems over time, they are returned in their original condition, although initially it seemed that they only tend towards chaos. Such cycle is called a Poincare cycle.

This begs a very interesting idea. Yes, indeed, the gas from the exploding helium balls in one pile not going back, but what if you wait even longer? What if the Poincare cycle for such a system is very large? There are entire cosmological models based on the hypothesis of the return of Poincare, one of them belongs to the famous mathematician Penrose. According to him, the universe first expands, then shrinks back, then explodes, expands and re-collapses, repeating exactly the previous cycle.
But this theory of cyclic Universe there is a big disadvantage: we don't know the processes are able to force the Universe to collapse. Where to find them? How well do we know our Universe? The data of the Planck telescope revealed that approximately 98% of the energy of our Universe is not concluded in the stars and in the ordinary matter from which we are composed. We barely know only about 2% of our Universe, and the rest of 98% do not know anything at all. That is, if we imagine that our universe is a big beautiful castle with towers, bridges, throne rooms and things, from the basement, we have not yet come out, and who knows what mysteries await us there. published
Author: Hayk Hakobyan
P. S. And remember, only by changing their consumption — together we change the world! ©
Join us in Facebook , Vkontakte, Odnoklassniki
Source: theoryandpractice.ru/posts/12510-chaos
What happens when we set in motion a pendulum? He begins to waver, each time decreasing amplitude. After a while we discover that the pendulum has stopped. But where did the energy of the pendulum? Those in the high school physics classes listened to the teacher attentively, answer, that energy will take away the air molecules. But why not the reverse? Why do molecules suddenly can't get together and, conversely, transmit energy to the pendulum?
The fact that the desire of the world to chaos is a fundamental property of nature. The directed movement of particles of the pendulum is converted into random motion of air molecules. Directed the flow of water sooner or later turn into a chaotic jet with turbulent eddies and meandering, interwoven with each other flows.

Our nature seeks vengeance to chaos, but is it really the desire of the infinite? At some point the system reaches some kind of peace? At what point is the desire stop? In the nineteenth century, Maxwell and a number of other physicists have shown that if you leave the system alone, it really comes to a certain state of "peace". This condition is called equilibrium, and in order to understand it, you need to forget about the individual rates, the coordinate of each particle and take a look at some collective characteristics of the system. For example, the number of particles at the moment have a certain speed.
If we plot the number of particles with velocity, we see an amazing thing: the system from any state, whatever this state was initially, in the end comes to one specific distribution of the number of particles with velocity, which is called the Maxwell distribution. This state is the ultimate destination of any system, and it achieves maximum chaos.

But... How do we measure chaos? In physics for measuring chaos using the value called the entropy of the system. The more entropy, the less ordered system. In equilibrium the entropy is maximum. Boltzmann in the XIX century was proved the so-called H-theorem, which States that in a closed system entropy over time always increases.

In practice, this is a quite clear of the consequences. If we, for example, take a balloon with helium and blow it into the corner of the room, the gas after some time will spread throughout the room, evenly filling the entire area. Thus, the entropy of the gas will increase and... Yes, in General, that's all. No matter how long we waited, helium will never going back to the pile in the corner of the room. That is, the processes in our world are irreversible: from the goal state we can not know the initial as the final state is the same for all initial States. This is understandable, our experience is quite corresponds. It is always easier to break something than to build, easier to scatter than to gather together. It's all quite logical, right?
Not really. Imagine that you have a closed room with a bunch of balls that fly and bump into each other. Everything is absolutely perfect, elastic collision, no energy loss. After a sufficient amount of time, the velocity distribution is exactly the Maxwell, entropy irreversibly increases to the maximum.
The data of the Planck telescope revealed that approximately 98% of the energy of our Universe is not concluded in the stars and in the ordinary matter, from which we But let's look at each bulb individually. The fact that for each ball we can know exactly its speed and coordinate, but also acting on it force. From Newton's second law can know the acceleration and the motion of each individual particles can clearly ask. Newton's law is time-reversible, as if to turn back time, its form does not amend the law. This means that the movement of each individual ball is also reversible: the final state of the ball can understand where he came from and how to move, but... the movement of all the balls together is irreversible.

That is the basis of our world are irreversible is quite a reversible laws. This is very strange. What if no irreversibility there, and it's just an illusion? What if the movement is just so complicated that it seems chaotic, but actually it quite regularly?
For an example of what I mean, let's take a very interesting system. It's called a cellular automaton. Imagine your universe is a simple series of white and black squares. You — the God of this Universe, and you need to lay down some rule of evolution at the time. And you are laying a very simple rule: if the cell itself is black and the neighboring two cells is also black, in the next step, the cell will be white (pictured bottom left), if the cell is black, its left neighbor is also black, and the neighbor on the right is white, then in the next step the cell will become black and so on. Thus it is possible to set a universal rule (the physics of your Universe. To record the act using zeros and ones or, if we translate them into a decimal record using just one number. In this case (in the picture) this is the rule 90. The evolution of this cellular automaton are shown below.

Such rules exist very much. There are rules, which are based on the previous two steps instead of one or multiple neighbors. There are rules for two-dimensional cellular automaton, where we have now not a number of black and white cells, and a plane.
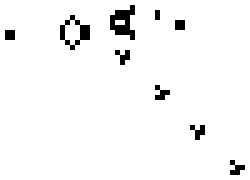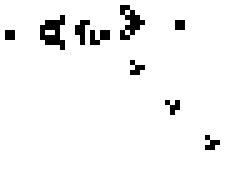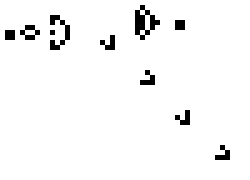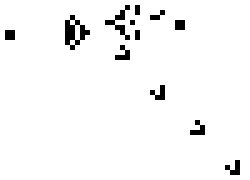
With the help of cellular automata is already getting quite complex, unpredictable shape — they are used in architecture and game design to build a realistic landscape. But, surprisingly, all this diversity, these unpredictable shapes and figures are defined only by a rule from one number, everything else is a matter of time.

But what if the diversity of our world, all the complex images created by our nature and all the chaos towards which our world is merely the implementation of a cellular automaton? What if we are merely a simulation of a cellular automaton in someone's computer?
As we learned in the first part, at the deepest core of our world are completely reversible laws, where at the end you can restore the initial one. Therefore, if the world is a cellular automaton, it must also be reversible. Such cellular automata really is, but they have one problem. Any reversible cellular automaton has a cycle: after a certain number of steps, the universe is recreated in its original form again, then again and so moves in a cycle.
In our world, unfortunately, this is not... Or is there? French mathematician Henri Poincare for certain types of systems noticed an interesting thing: as a result of the evolution of these systems over time, they are returned in their original condition, although initially it seemed that they only tend towards chaos. Such cycle is called a Poincare cycle.

This begs a very interesting idea. Yes, indeed, the gas from the exploding helium balls in one pile not going back, but what if you wait even longer? What if the Poincare cycle for such a system is very large? There are entire cosmological models based on the hypothesis of the return of Poincare, one of them belongs to the famous mathematician Penrose. According to him, the universe first expands, then shrinks back, then explodes, expands and re-collapses, repeating exactly the previous cycle.
But this theory of cyclic Universe there is a big disadvantage: we don't know the processes are able to force the Universe to collapse. Where to find them? How well do we know our Universe? The data of the Planck telescope revealed that approximately 98% of the energy of our Universe is not concluded in the stars and in the ordinary matter from which we are composed. We barely know only about 2% of our Universe, and the rest of 98% do not know anything at all. That is, if we imagine that our universe is a big beautiful castle with towers, bridges, throne rooms and things, from the basement, we have not yet come out, and who knows what mysteries await us there. published
Author: Hayk Hakobyan
P. S. And remember, only by changing their consumption — together we change the world! ©
Join us in Facebook , Vkontakte, Odnoklassniki
Source: theoryandpractice.ru/posts/12510-chaos