590
只是复杂的:为什么一切都倾向于混乱,以及如何停止它
有时当你觉得升级的熵,但我不知道为什么,答案在于物理:渴望的世界混乱是一个基本的财产的性质。 什么是混乱的,让我们做它,它可以以某种方式测量,以及为什么有表述"打破的—不建立"吗? 所有这一切都解释为一个科学记者,一个部门员工的物理学和天体物理学参考和笔记海伊克Hakobyan的。
会发生什么,当我们在运动设置一个钟摆? 他开始动摇,每个时间减少的幅度。 一段时间后,我们发现这个钟摆已经停止。 但是,在没有能摆? 那些在高中物理课听到的教师聚精会神,答案,那能量就会取走了空气分子。 但是,为什么不倒? 为什么分子突然不能在一起,相反,发射能摆?
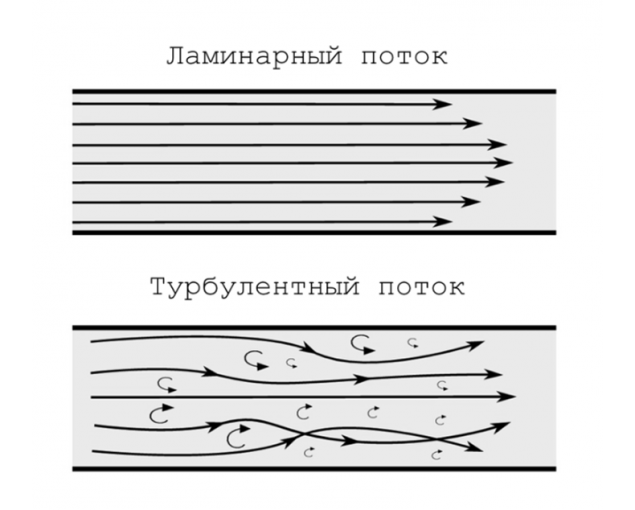
事实上,渴望的世界混乱是一个基本的财产的性质。 向移动的微粒摆转变成随意运动的空气分子。 引导的水的流动或早或晚变成一个混乱的机与动荡的漩涡和曲折的,交织在一起的每一个其它流动。
我们的自然寻求报复到混乱,但是它真的希望无限吗? 在某一点的系统达到某种和平? 在什么时候是希望停止吗? 在十九世纪的,麦克斯韦和一些其他的物理学家已经显示,如果保留该系统的单独的,它真正地涉及到一个特定国家的"和平"。 这种情况被称为平衡,并为了理解它,你需要要忘了个别的费率,协调的每个颗粒和看一看一些集体特性的系统。 例如,数的粒子在那一刻,有一定的速度。
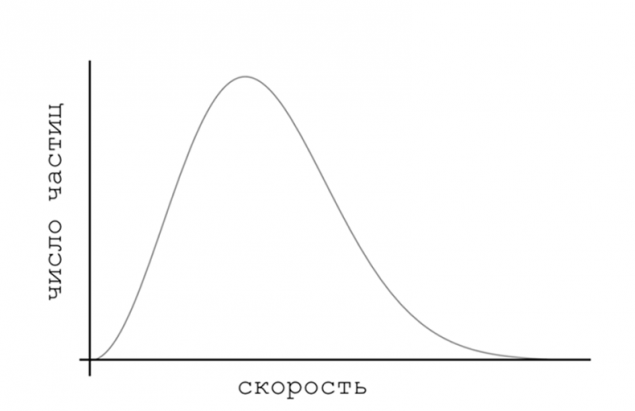
如果我们绘制的数量颗粒的速度,我们看到一个惊人的事情:该系统自任何国家,无论这种状态是最初的,在结束涉及到一个特定的分配数量颗粒的速度,这就是所谓的麦克斯韦的分布。 这种状态是最终目的地的任何系统,它达到了最大的混乱。
但是...我们如何衡量混乱? 在物理测量的混乱使用价值被称为熵的系统。 更多的熵、较少购系统。 在平衡的熵是最大的。 玻尔兹曼在十九世纪是证明所谓H-理论,其中指出,在一个封闭的系统熵随着时间一直增加。
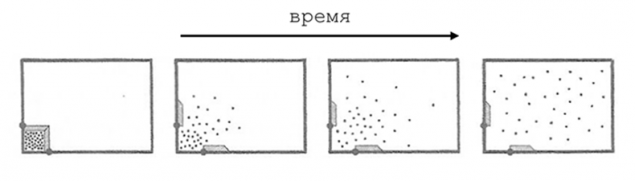
在实践中,这是一个很清楚的后果。 如果我们的,例如,采取一个囊用氦气吹进入房间的角落里,该气体在一段时间之后将会传遍了整个房间,平均灌整个区域。 因此,熵的天然气将增加,和...是的,在一般情况下,这就是全部。 无论如何,只要我们等待着,氦将永远不会回来一堆在房间的角落里. 也就是,该进程在我们的世界是不可逆转的:从目标国家,我们可能不知道最初作为最后状态是相同的所有初始国。 这是可以理解的,我们的经验是相当相对应。 它总是容易打破东西,而不是建立,更易于分散于聚集在一起。 这是所有相当符合逻辑,对吗?
不是真的。 想象一下,你有一个封闭的房间有一大堆球飞撞到彼此。 一切都是绝对完美的,弹性碰撞,不能丢失。 在足够的时间,速度分布正是Maxwell,熵不可逆转地增加到最大。
数据的马克斯*普朗克的望远镜揭示,约有98%的能量我们的宇宙不是结束的星星,并在普通问题,从我们的 但是让我们看看每个灯泡。 事实上,对每个球我们可以确切地知道它的速度和协调,但也采取行动的力量。 从牛顿第二法可以知道的加速度和运动的每个颗粒可以清楚的要求。 牛顿的法律是时候-可逆转的,因为如果返回时,其形式并不修改法律。 这意味着运动的每一个球也是可逆的:该最终状态球可以理解他是从哪里来的和如何移动,但是...运动的所有的球在一起是不可逆转的。
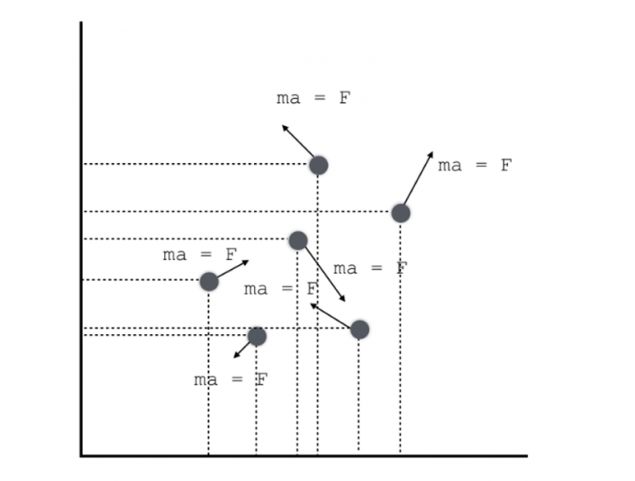
这是根据我们的世界是不可逆转是一个相当可逆转的法律。 这是非常奇怪的。 如果没有有不可逆转,并且这只是一种幻想吗? 如果有什么的运动就是这么复杂,它似乎混乱,但实际上它很经常吗?
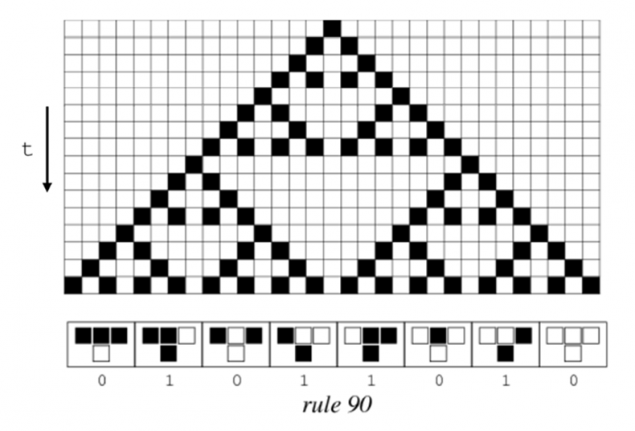
对于一个例子是什么我的意思是,让我们采取一个非常有趣的系统。 这就是所谓的蜂窝状自动机。 想象一下你的宇宙中是一个简单的系列的白色和黑色的正方形。 你的上帝这个宇宙,你需要放下些规则的演变的时候。 和你正在铺设一个非常简单的规则:如果细胞本身是黑色和邻近的两个单元也是黑色的,在下一个步骤,该单元将是白色的(如图左下),如果单元是黑色的,其左邻居也是黑色的,并且邻居的权利是白色的,然后在接下来的步骤的细胞将会变成黑色。 因此,它是可以设置一个普遍的规则(物理的宇宙。 记录的法使用零和的或者,如果我们把它们转化为一个小数记录仅使用一个数字。 在这种情况下(在图片)这是规则90. 的演变这个蜂窝式的自动机如下表所示。
这种规则的存在非常多。 有规则,它们是基于以前两个步骤,而不是一个或多个邻国。 有规则的两个维蜂窝状自动机,我们现在有没有一些黑人和白细胞、和飞机。
与帮助的蜂窝状自动机已经变得相当复杂的,不可预测的外形—他们是用于建筑和游戏的设计,以构建一个真实的景观。 但是,令人惊讶的是,所有这种多样性,这些不可预料的形状和数字的定义只有通过一个规则是从一个数目,其他一切都是时间的问题。
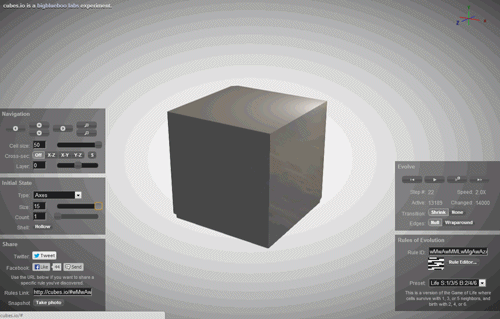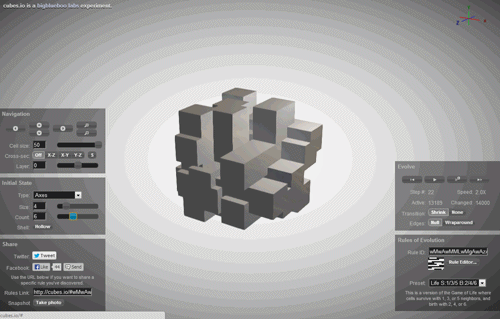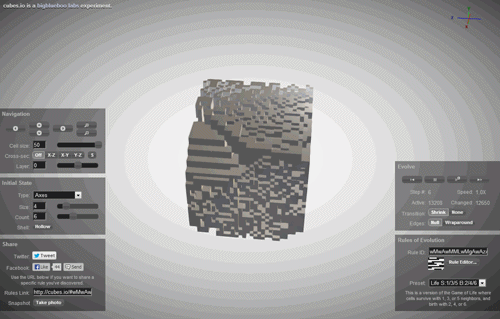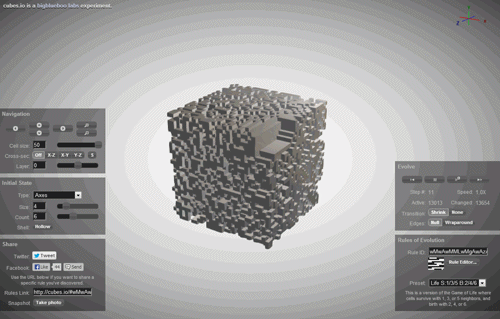
但是,如果多样化的世界中,所有复杂的图像我们的性质和所有的混乱对我们的世界仅仅是执行的一个蜂窝式的自动机? 如果我们仅仅是一个模拟的一个蜂窝式的自动机以某人的计算机?
作为我们学到的第一部分,在最深切的核心我们的世界是完全可逆的法律,在那里结束时,你可以恢复最初的一个。 因此,如果世界是一个蜂窝式的自动机,它也必须是可逆的。 这样的蜂窝状自动机真的是,但是他们有一个问题。 任何可逆胞自动具有周期:之后的一定数量的步骤,宇宙是重新在其原始形式再次,然后再次使移,在一个周期。
在我们的世界,不幸的是,这不是...或是在那里? 法国数学家亨利*庞加莱用于某些类型的系统,注意到一个有趣的事情:作为一个进化的结果,这些系统随着时间的推移,他们返回他们原来的条件,虽然最初看起来他们只是倾向于混乱。 这样的循环中被称为一个庞加莱循环。

这引出了一个非常有趣的想法。 是的,事实上,气体从爆炸氦气球在一桩不会回去的,但是如果你等待更长的时间? 如果有什么庞加莱周期对于这样一个系统是非常大? 那是整个宇宙模型基于假设的返回的庞加莱,他们中的一个属于着名的数学家彭罗斯的。 根据他的说法,宇宙的第一扩展,然后收缩回去,然后爆炸,扩展和重新崩溃,完全重复前一个周期。
但是,这一理论的环宇宙里有一个很大的缺点:我们不知道的进程能力的宇宙来的崩溃。 在哪里可以找到他们吗? 怎么那么我们知道我们的宇宙? 数据的马克斯*普朗克的望远镜揭示,约有98%的能量我们的宇宙不是结束的星星,并在普通问题,从我们组成。 我们几乎不知道,只有约2%,我们的宇宙,而其余的98%不知道任何事情。 也就是说,如果我们想象一下,我们的宇宙中是一个美丽的大城堡与塔、桥梁、宝座房和的事情,从地下室,我们尚未出来了,谁知道什么秘密等待着我们。 出版
作者:海伊克Hakobyan
P.S.记住,仅仅通过改变他们的消费—我们一起改变世界了。 ©
加入我们在Facebook,脸谱了,语音
资料来源:theoryandpractice.ru/posts/12510-chaos
会发生什么,当我们在运动设置一个钟摆? 他开始动摇,每个时间减少的幅度。 一段时间后,我们发现这个钟摆已经停止。 但是,在没有能摆? 那些在高中物理课听到的教师聚精会神,答案,那能量就会取走了空气分子。 但是,为什么不倒? 为什么分子突然不能在一起,相反,发射能摆?
事实上,渴望的世界混乱是一个基本的财产的性质。 向移动的微粒摆转变成随意运动的空气分子。 引导的水的流动或早或晚变成一个混乱的机与动荡的漩涡和曲折的,交织在一起的每一个其它流动。

我们的自然寻求报复到混乱,但是它真的希望无限吗? 在某一点的系统达到某种和平? 在什么时候是希望停止吗? 在十九世纪的,麦克斯韦和一些其他的物理学家已经显示,如果保留该系统的单独的,它真正地涉及到一个特定国家的"和平"。 这种情况被称为平衡,并为了理解它,你需要要忘了个别的费率,协调的每个颗粒和看一看一些集体特性的系统。 例如,数的粒子在那一刻,有一定的速度。
如果我们绘制的数量颗粒的速度,我们看到一个惊人的事情:该系统自任何国家,无论这种状态是最初的,在结束涉及到一个特定的分配数量颗粒的速度,这就是所谓的麦克斯韦的分布。 这种状态是最终目的地的任何系统,它达到了最大的混乱。

但是...我们如何衡量混乱? 在物理测量的混乱使用价值被称为熵的系统。 更多的熵、较少购系统。 在平衡的熵是最大的。 玻尔兹曼在十九世纪是证明所谓H-理论,其中指出,在一个封闭的系统熵随着时间一直增加。

在实践中,这是一个很清楚的后果。 如果我们的,例如,采取一个囊用氦气吹进入房间的角落里,该气体在一段时间之后将会传遍了整个房间,平均灌整个区域。 因此,熵的天然气将增加,和...是的,在一般情况下,这就是全部。 无论如何,只要我们等待着,氦将永远不会回来一堆在房间的角落里. 也就是,该进程在我们的世界是不可逆转的:从目标国家,我们可能不知道最初作为最后状态是相同的所有初始国。 这是可以理解的,我们的经验是相当相对应。 它总是容易打破东西,而不是建立,更易于分散于聚集在一起。 这是所有相当符合逻辑,对吗?
不是真的。 想象一下,你有一个封闭的房间有一大堆球飞撞到彼此。 一切都是绝对完美的,弹性碰撞,不能丢失。 在足够的时间,速度分布正是Maxwell,熵不可逆转地增加到最大。
数据的马克斯*普朗克的望远镜揭示,约有98%的能量我们的宇宙不是结束的星星,并在普通问题,从我们的 但是让我们看看每个灯泡。 事实上,对每个球我们可以确切地知道它的速度和协调,但也采取行动的力量。 从牛顿第二法可以知道的加速度和运动的每个颗粒可以清楚的要求。 牛顿的法律是时候-可逆转的,因为如果返回时,其形式并不修改法律。 这意味着运动的每一个球也是可逆的:该最终状态球可以理解他是从哪里来的和如何移动,但是...运动的所有的球在一起是不可逆转的。

这是根据我们的世界是不可逆转是一个相当可逆转的法律。 这是非常奇怪的。 如果没有有不可逆转,并且这只是一种幻想吗? 如果有什么的运动就是这么复杂,它似乎混乱,但实际上它很经常吗?
对于一个例子是什么我的意思是,让我们采取一个非常有趣的系统。 这就是所谓的蜂窝状自动机。 想象一下你的宇宙中是一个简单的系列的白色和黑色的正方形。 你的上帝这个宇宙,你需要放下些规则的演变的时候。 和你正在铺设一个非常简单的规则:如果细胞本身是黑色和邻近的两个单元也是黑色的,在下一个步骤,该单元将是白色的(如图左下),如果单元是黑色的,其左邻居也是黑色的,并且邻居的权利是白色的,然后在接下来的步骤的细胞将会变成黑色。 因此,它是可以设置一个普遍的规则(物理的宇宙。 记录的法使用零和的或者,如果我们把它们转化为一个小数记录仅使用一个数字。 在这种情况下(在图片)这是规则90. 的演变这个蜂窝式的自动机如下表所示。

这种规则的存在非常多。 有规则,它们是基于以前两个步骤,而不是一个或多个邻国。 有规则的两个维蜂窝状自动机,我们现在有没有一些黑人和白细胞、和飞机。
与帮助的蜂窝状自动机已经变得相当复杂的,不可预测的外形—他们是用于建筑和游戏的设计,以构建一个真实的景观。 但是,令人惊讶的是,所有这种多样性,这些不可预料的形状和数字的定义只有通过一个规则是从一个数目,其他一切都是时间的问题。

但是,如果多样化的世界中,所有复杂的图像我们的性质和所有的混乱对我们的世界仅仅是执行的一个蜂窝式的自动机? 如果我们仅仅是一个模拟的一个蜂窝式的自动机以某人的计算机?
作为我们学到的第一部分,在最深切的核心我们的世界是完全可逆的法律,在那里结束时,你可以恢复最初的一个。 因此,如果世界是一个蜂窝式的自动机,它也必须是可逆的。 这样的蜂窝状自动机真的是,但是他们有一个问题。 任何可逆胞自动具有周期:之后的一定数量的步骤,宇宙是重新在其原始形式再次,然后再次使移,在一个周期。
在我们的世界,不幸的是,这不是...或是在那里? 法国数学家亨利*庞加莱用于某些类型的系统,注意到一个有趣的事情:作为一个进化的结果,这些系统随着时间的推移,他们返回他们原来的条件,虽然最初看起来他们只是倾向于混乱。 这样的循环中被称为一个庞加莱循环。

这引出了一个非常有趣的想法。 是的,事实上,气体从爆炸氦气球在一桩不会回去的,但是如果你等待更长的时间? 如果有什么庞加莱周期对于这样一个系统是非常大? 那是整个宇宙模型基于假设的返回的庞加莱,他们中的一个属于着名的数学家彭罗斯的。 根据他的说法,宇宙的第一扩展,然后收缩回去,然后爆炸,扩展和重新崩溃,完全重复前一个周期。
但是,这一理论的环宇宙里有一个很大的缺点:我们不知道的进程能力的宇宙来的崩溃。 在哪里可以找到他们吗? 怎么那么我们知道我们的宇宙? 数据的马克斯*普朗克的望远镜揭示,约有98%的能量我们的宇宙不是结束的星星,并在普通问题,从我们组成。 我们几乎不知道,只有约2%,我们的宇宙,而其余的98%不知道任何事情。 也就是说,如果我们想象一下,我们的宇宙中是一个美丽的大城堡与塔、桥梁、宝座房和的事情,从地下室,我们尚未出来了,谁知道什么秘密等待着我们。 出版
作者:海伊克Hakobyan
P.S.记住,仅仅通过改变他们的消费—我们一起改变世界了。 ©
加入我们在Facebook,脸谱了,语音
资料来源:theoryandpractice.ru/posts/12510-chaos