591
Просто про складно: чому все навколо прагне до хаосу і як його зупинити
Коли ви іноді відчуваєте рівень ентропії, але не розумієте, чому відповідь лежить в фізиці: прагнення світу до хаосу є фундаментальною властивістю природи. Що таке хаос, чи можна його вимірювати інакше, і чому існує вираз «розрив»? Про це розповів науковий журналіст, співробітник відділу фізики та астрофізики МРТ Гайк Хакобиан.
Що відбувається, коли ми встановлюємо ручку в русі? Починається коливатися, кожен раз зменшуючи амплітуду. Після того, як ми знаходимо, що припинили ручку. Але де з'явилася енергія полю? Ті, хто уважно слухав вчителя в класах фізики в школі, відповімо, що енергія буде відхилена молекулами повітря. Але чому не буває навпаки? Чому не можна молекул, що раптово збирають і переносять енергію на подол?
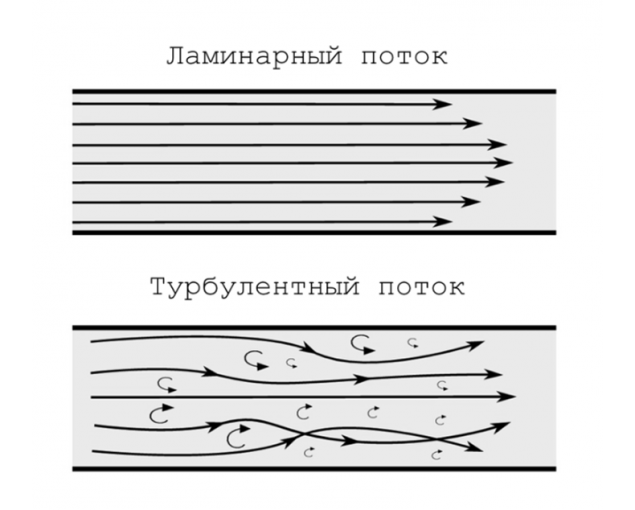
У світі бажання хаосу є фундаментальною рисою природи. Напрямний рух породових частинок перетворюється в хаотичний рух молекул повітря. Напрямний потік води скорочиться або пізніше перетвориться в хаотичний струмінь з турбулентними вихами і скручування, переплетені витрати.
Наша природа прагне до хаосу, але це прагнення нескінченно? Яким чином система досягає миру? Яким чином це бажання перестати? У дев'ятнадцятому столітті Максвелл і ряд інших фізиків показали, що якщо ви залишаєте систему самостійно, вона дійсно доходить до певного стану «кальмарності». Цей стан називається рівновагою, і розуміти його, потрібно забувати про індивідуальну швидкість, координати кожної частинки і подивитися на деякі колективні характеристики системи. Наприклад, скільки частинок мають певну швидкість.
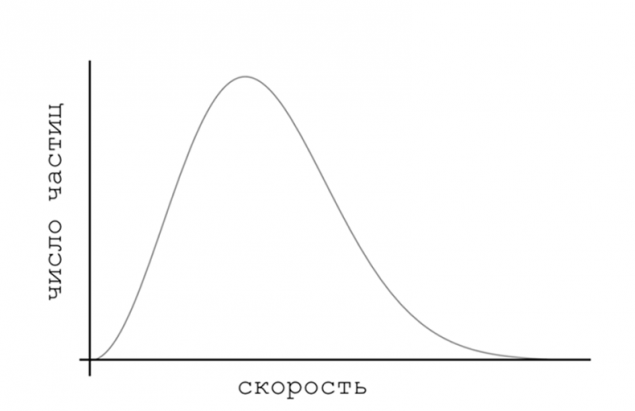
Якщо ми поділяємо кількість частинок від швидкості, ми бачимо дивовижну річ: система від будь-якого стану, що його оригінальний стан, в кінцевому підсумку прибуває в одному конкретному розподілі кількості частинок від швидкості, яка називається розподілом Maxwell. Цей стан є кінцевим пунктом призначення будь-якої системи і максимізує хаос.
Але... Як ви навіть вимірюєте хаос? У фізиці використовується кількість ентропії системи для вимірювання хаосу. Чим більша ентропія, тим менше замовляє система. У рівновагі максимальна ентропія. Болтзманн в XIX столітті довів так звану Г-теорем, яка стверджує, що в закритій системі ентропія завжди зростає з часом.
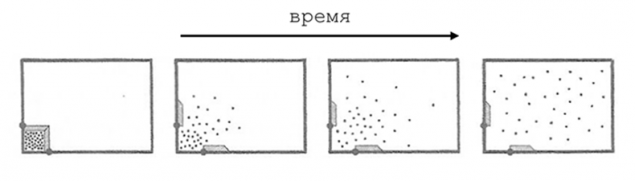
На практиці це зрозумілі наслідки. Якщо, наприклад, ми беремо кульку гелію і вдаримо її в кут приміщення, газ з часом пошириться по всій кімнаті, наповнивши його рівномірно. Таким чином, ентропія газу підвищиться до максимального і того, що є. Неважливо, як довго ми чекаємо, гелій ніколи не повернуться разом в кутку приміщення. Це, процеси в нашому світі незворотні: від остаточного стану ми не можемо знати початковий, оскільки кінцевий стан є однаковим для всіх початкових станів. Ми можемо самі зателефонувати одержувачу. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. Що робить ідеальний сенс, правильно?
Не точно. Уявіть, що у вас є закритий номер з пучком м'ячів, які літають і збиваються один одному. Все ідеально, зіткнення пружні, не втрати енергії. Після достатньої кількості часу розподіл оксамитових місць буде точно Maxwellian, ентропія незворотно збільшиться до максимуму.
Дані з телескопа Planck показали, що приблизно 98% енергії нашого Всесвіту не містяться в зірках і в звичайній матерії яких ми складається. Але давайте подивимося на кожну кульку індивідуально. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. З другого закону Ньютона ми можемо дізнатися прискорення, і це все: рух кожної окремої частинки можна точно визначити. Закон Ньютона – це своєчасне, тому що якщо час вимкнено, закон не змінить його форму. Це означає, що рух кожного окремого м'яча також є реверсивним: від остаточного стану м'яча ви можете зрозуміти, де він прийшов з і як він переїхав. Але рух всіх кульок незворотний.
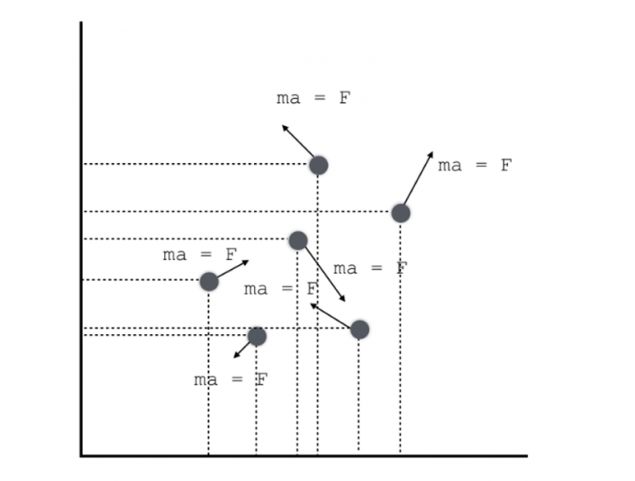
Це, в самому серці нашого незворотного світу, досить незворотні закони. Дуже дивний. Що робити, якщо немає незворотності, і це просто ілюзія? Що, якщо рух просто так складний, що нам здається хаотичною, коли насправді це досить регулярне?
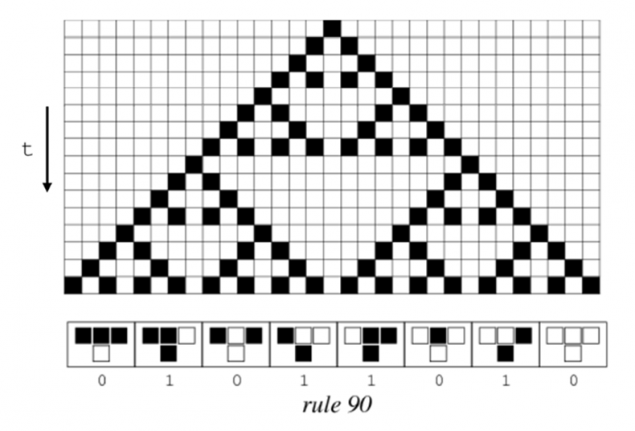
Наприклад, ми беремо дуже цікава система. Це називається стільниковим автоматоном. Уявіть, що ваш Всесвіт - це простий ряд білих і чорних клітин. Ви є богом цього Всесвіту, і вам потрібно укладати деякі правила еволюції протягом часу. І ви кладете дуже просте правило: якщо сама клітинка чорна і сусідні дві клітини також чорні, то в наступному кроці клітинка буде білою (зображена зліва внизу), якщо клітина чорна, сусід зліва також чорна, а сусід на правому білому, то в наступному кроці клітинка стане чорним і так далі. Таким чином, ви можете встановити універсальне правило (фізика) вашого Всесвіту. Ви можете написати цей закон за допомогою нулів і, або, якщо ви перевести їх в десятковий запис, з просто одним номером. У цьому випадку (зображений) він буде руль 90. Еволюція такого клітинного автоматону показано нижче.
Є багато таких правил. На попередніх двох кроках, замість одного або декількох сусідів. Є правила двовимірного стільникового автомата, де ми більше не маємо ряд чорних і білих клітин, але ціла площина.
За допомогою стільникового автомата вже отримані повністю складні, непередбачувані фігури - вони використовуються в архітектурі і ігровому дизайні, щоб побудувати реалістичний пейзаж. Але що дивно, що все це різноманітність, всі ці непередбачувані форми і зображення є лише правилом одного числа, все інше - справа часу.
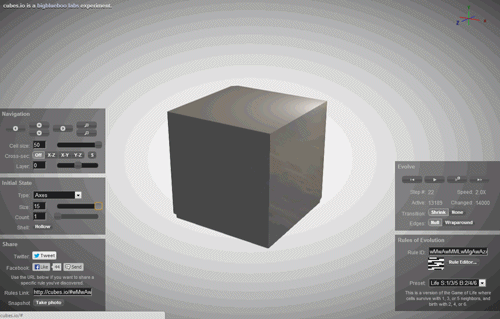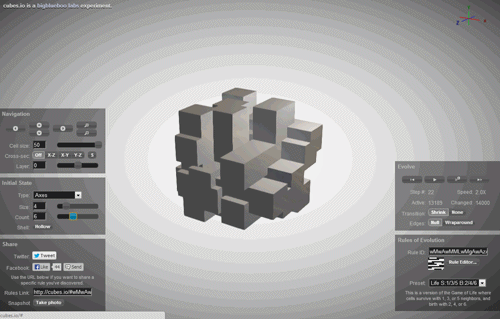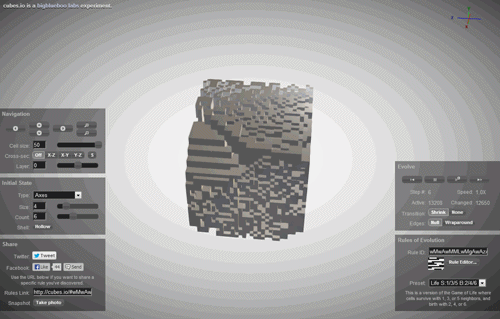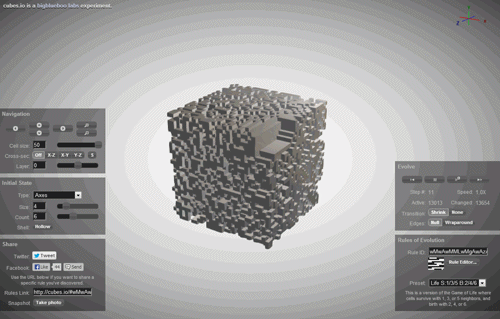
Але що якщо все різноманіття нашого світу, всі складні зображення, створені нашою природою, і всі хаоси, які наш світ прагне, є просто втіленням деяких клітинних автоматонів? Що робити, якщо ми були просто імітацією клітинного автоматону в комп’ютері?
Як ми побачили в першій частині, на найглибшому фундаменті нашого світу повністю реверсивні закони, де в кінцевому стані можна відновити оригінальні. Тому, якщо світ є стільниковим автоматоном, він також повинен бути оборотним. Такі клітинні автомати існують, але вони мають одну проблему. Будь-який реверсивний стільниковий автоматон має цикл: після певної кількості кроків, всесвіт знову відтворює свою оригінальну форму, потім знову - і рухається так по циклу.
На жаль, немає такої речі в нашому світі... Чи є? Французька математика Анрі Поінкаре помітила цікаве для певного типу системи: в результаті еволюції цих систем вони в кінцевому підсумку повернулися до свого первісного стану, хоча вони спочатку здавалося б, тільки до хаосу. Цей цикл називається Poincaré цикл.

Це дуже цікава ідея. Так, дійсно, газ від вибухових гелійських кульок не вийде разом в одній палі, але що якщо ви очікуєте ще довше? Що робити, якщо Poincaré цикл для такої системи є дуже великим? На основі гіпотези повернення Poincaré, одна з яких належить знаменитому математику Penrose. На його думку, Всесвіт спочатку переповнений, після чого згортається назад, потім знову вибухає, знову запалюється і згортається, повторюючи точно попередній цикл.
Але ця теорія циклічного Всесвіту має великий недолік: ми ще не знаємо процеси, які можуть викликати Всесвіт, щоб згорнути. Де знайти їх? Як ми знаємо наш Всесвіт, який добре? Дані з телескопа Planck показали, що близько 98% енергії нашого Всесвіту не містяться в зірках або в звичайній матерії, що робить нас. Ми знаємо тільки про 2% нашого Всесвіту, а про інші 98% ми знаємо нічого. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз.
Автор: Хайк Хакобиан
P.S. І пам'ятаєте, просто змінивши наше споживання – разом ми змінюємо світ!
Приєднуйтесь до нас на Facebook, VKontakte, Odnoklassniki
Джерело: теоріяandpractice.ru/posts/12510-chaos
Що відбувається, коли ми встановлюємо ручку в русі? Починається коливатися, кожен раз зменшуючи амплітуду. Після того, як ми знаходимо, що припинили ручку. Але де з'явилася енергія полю? Ті, хто уважно слухав вчителя в класах фізики в школі, відповімо, що енергія буде відхилена молекулами повітря. Але чому не буває навпаки? Чому не можна молекул, що раптово збирають і переносять енергію на подол?
У світі бажання хаосу є фундаментальною рисою природи. Напрямний рух породових частинок перетворюється в хаотичний рух молекул повітря. Напрямний потік води скорочиться або пізніше перетвориться в хаотичний струмінь з турбулентними вихами і скручування, переплетені витрати.

Наша природа прагне до хаосу, але це прагнення нескінченно? Яким чином система досягає миру? Яким чином це бажання перестати? У дев'ятнадцятому столітті Максвелл і ряд інших фізиків показали, що якщо ви залишаєте систему самостійно, вона дійсно доходить до певного стану «кальмарності». Цей стан називається рівновагою, і розуміти його, потрібно забувати про індивідуальну швидкість, координати кожної частинки і подивитися на деякі колективні характеристики системи. Наприклад, скільки частинок мають певну швидкість.
Якщо ми поділяємо кількість частинок від швидкості, ми бачимо дивовижну річ: система від будь-якого стану, що його оригінальний стан, в кінцевому підсумку прибуває в одному конкретному розподілі кількості частинок від швидкості, яка називається розподілом Maxwell. Цей стан є кінцевим пунктом призначення будь-якої системи і максимізує хаос.

Але... Як ви навіть вимірюєте хаос? У фізиці використовується кількість ентропії системи для вимірювання хаосу. Чим більша ентропія, тим менше замовляє система. У рівновагі максимальна ентропія. Болтзманн в XIX столітті довів так звану Г-теорем, яка стверджує, що в закритій системі ентропія завжди зростає з часом.

На практиці це зрозумілі наслідки. Якщо, наприклад, ми беремо кульку гелію і вдаримо її в кут приміщення, газ з часом пошириться по всій кімнаті, наповнивши його рівномірно. Таким чином, ентропія газу підвищиться до максимального і того, що є. Неважливо, як довго ми чекаємо, гелій ніколи не повернуться разом в кутку приміщення. Це, процеси в нашому світі незворотні: від остаточного стану ми не можемо знати початковий, оскільки кінцевий стан є однаковим для всіх початкових станів. Ми можемо самі зателефонувати одержувачу. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. Що робить ідеальний сенс, правильно?
Не точно. Уявіть, що у вас є закритий номер з пучком м'ячів, які літають і збиваються один одному. Все ідеально, зіткнення пружні, не втрати енергії. Після достатньої кількості часу розподіл оксамитових місць буде точно Maxwellian, ентропія незворотно збільшиться до максимуму.
Дані з телескопа Planck показали, що приблизно 98% енергії нашого Всесвіту не містяться в зірках і в звичайній матерії яких ми складається. Але давайте подивимося на кожну кульку індивідуально. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. З другого закону Ньютона ми можемо дізнатися прискорення, і це все: рух кожної окремої частинки можна точно визначити. Закон Ньютона – це своєчасне, тому що якщо час вимкнено, закон не змінить його форму. Це означає, що рух кожного окремого м'яча також є реверсивним: від остаточного стану м'яча ви можете зрозуміти, де він прийшов з і як він переїхав. Але рух всіх кульок незворотний.

Це, в самому серці нашого незворотного світу, досить незворотні закони. Дуже дивний. Що робити, якщо немає незворотності, і це просто ілюзія? Що, якщо рух просто так складний, що нам здається хаотичною, коли насправді це досить регулярне?
Наприклад, ми беремо дуже цікава система. Це називається стільниковим автоматоном. Уявіть, що ваш Всесвіт - це простий ряд білих і чорних клітин. Ви є богом цього Всесвіту, і вам потрібно укладати деякі правила еволюції протягом часу. І ви кладете дуже просте правило: якщо сама клітинка чорна і сусідні дві клітини також чорні, то в наступному кроці клітинка буде білою (зображена зліва внизу), якщо клітина чорна, сусід зліва також чорна, а сусід на правому білому, то в наступному кроці клітинка стане чорним і так далі. Таким чином, ви можете встановити універсальне правило (фізика) вашого Всесвіту. Ви можете написати цей закон за допомогою нулів і, або, якщо ви перевести їх в десятковий запис, з просто одним номером. У цьому випадку (зображений) він буде руль 90. Еволюція такого клітинного автоматону показано нижче.

Є багато таких правил. На попередніх двох кроках, замість одного або декількох сусідів. Є правила двовимірного стільникового автомата, де ми більше не маємо ряд чорних і білих клітин, але ціла площина.
За допомогою стільникового автомата вже отримані повністю складні, непередбачувані фігури - вони використовуються в архітектурі і ігровому дизайні, щоб побудувати реалістичний пейзаж. Але що дивно, що все це різноманітність, всі ці непередбачувані форми і зображення є лише правилом одного числа, все інше - справа часу.

Але що якщо все різноманіття нашого світу, всі складні зображення, створені нашою природою, і всі хаоси, які наш світ прагне, є просто втіленням деяких клітинних автоматонів? Що робити, якщо ми були просто імітацією клітинного автоматону в комп’ютері?
Як ми побачили в першій частині, на найглибшому фундаменті нашого світу повністю реверсивні закони, де в кінцевому стані можна відновити оригінальні. Тому, якщо світ є стільниковим автоматоном, він також повинен бути оборотним. Такі клітинні автомати існують, але вони мають одну проблему. Будь-який реверсивний стільниковий автоматон має цикл: після певної кількості кроків, всесвіт знову відтворює свою оригінальну форму, потім знову - і рухається так по циклу.
На жаль, немає такої речі в нашому світі... Чи є? Французька математика Анрі Поінкаре помітила цікаве для певного типу системи: в результаті еволюції цих систем вони в кінцевому підсумку повернулися до свого первісного стану, хоча вони спочатку здавалося б, тільки до хаосу. Цей цикл називається Poincaré цикл.

Це дуже цікава ідея. Так, дійсно, газ від вибухових гелійських кульок не вийде разом в одній палі, але що якщо ви очікуєте ще довше? Що робити, якщо Poincaré цикл для такої системи є дуже великим? На основі гіпотези повернення Poincaré, одна з яких належить знаменитому математику Penrose. На його думку, Всесвіт спочатку переповнений, після чого згортається назад, потім знову вибухає, знову запалюється і згортається, повторюючи точно попередній цикл.
Але ця теорія циклічного Всесвіту має великий недолік: ми ще не знаємо процеси, які можуть викликати Всесвіт, щоб згорнути. Де знайти їх? Як ми знаємо наш Всесвіт, який добре? Дані з телескопа Planck показали, що близько 98% енергії нашого Всесвіту не містяться в зірках або в звичайній матерії, що робить нас. Ми знаємо тільки про 2% нашого Всесвіту, а про інші 98% ми знаємо нічого. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз.
Автор: Хайк Хакобиан
P.S. І пам'ятаєте, просто змінивши наше споживання – разом ми змінюємо світ!
Приєднуйтесь до нас на Facebook, VKontakte, Odnoklassniki
Джерело: теоріяandpractice.ru/posts/12510-chaos