835
10 Логічні парадокси
Якщо ви не повністю плутаєтеся, прочитавши цю колекцію, ви не думаєте явно 
Вчені і мислики довго люблять зберігати себе і колеги, встановлюючи нерозчинні проблеми і формулюючи різні види парадоксів. Деякі з цих думаних експериментів залишаються актуальними протягом тисяч років, що вказують на імперфікацію багатьох популярних наукових моделей і отворів в звичайних теоріях, які давно розглядаються фундаментальними. Ми запрошуємо Вас відобразити на найцікавіших і дивовижних парадоксах, які, як кажуть, тепер, «знижувати мозок» більш ніж одного покоління логиків, філософів і математиків.
1,1 км Парадокс Ахіллс і черепаха є однією з апоріїв (логічно правильних, але суперечливих виписок) сформульовані давньогрецьким філософом Zeno Eleia в п'ятому столітті до н. е. Його суть полягає в тому, що легендарний герой Achilles вирішив конкурувати з черепахою. Як ви знаєте, черепахи не відрізняються швидкістю, тому Ахілли дали супротивнику старт 500 м. Коли черепаха долає цю дистанцію, герой переходить в переслідування на швидкості 10 разів більше, тобто, в той час як черепаха crawls 50 м, Achilles керує запуску 500 м голови. Потім бігун подолає наступну 50 м, але черепаху в цей час crawls ще 5 м, здається, що Achilles є про те, щоб зловити її, але опонент все ще попереду і в той час як він працює 5 м, вона керується заздалегідь ще півметра і так далі. Відстань між ними нескінченно знижується, але в теорії герой не вдається зловити повільною черепицею, це небагато, але завжди попереду його.
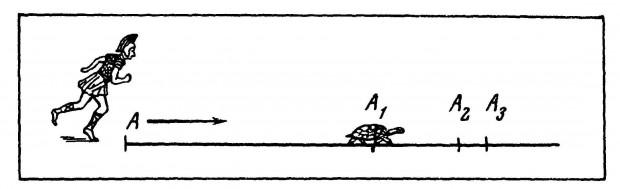
Звісно, з точки зору фізики, парадокс не має сенсу – якщо Achilles рухається набагато швидше, він в будь-якому випадку зламається вперед, але Zeno бажав продемонструвати свої аргументи, що ідеалізовані математичні поняття «точності простору» і «момент часу» не дуже підходять для коректного застосування до реального руху. Апорія розкриває невідповідність між математично обґрунтованою ідеєю, яка незеро інтервалів простору і часу може бути розділена на невизначено (наприклад, черепаха повинна завжди йти вперед) і реальністю, в якій герой, звичайно, перемагає забіг.
2. Парадокс часу
Парадокс, що описує часову подорож, було джерелом натхнення для письменників і творців художньої літератури та серіалів. Є кілька варіантів парадоксів часової петлі, один з найпростіших і найбільш графічних прикладів такої проблеми був представлений у своїй книзі «Новий час подорожників» Девідом Тоомей, професором Університету Массачусетса.
Уявіть час мандрівника, купивши копію Шекспіра Хамлета у книжковому магазині. І пішов він в Англію під час царя Єлизавета І, після знаходження Вільяма Шекспіра, подав йому книгу. Він перевернув його і опублікував його як власну роботу. Сотні минулих років, Гамлет перекладається на десятки мов, безперечно передруковані, і один з примірників знаходиться в тому ж книжковому магазині, де час мандрівник купує його і дає йому шекспіру, і він робить копію і так далі. Хто є автором безсмертної трагедії?
3. У Дівчина і хлопець Paradox
У теорії ймовірності це парадокс також називається «Діти Мр. Сміту» або «Мр. проблеми Сміту». Вперше сформульовано американський математик Мартін Гарднер у питанні наукової Америки. Вчені обговорювали парадокс протягом десятиліть, і існує кілька способів її вирішення. Після мислення про проблему, ви можете запропонувати власний варіант.
Є два дітей в сім'ї і відомо, що один з них є хлопчиком. Яка ймовірність того, що друга дитина також чоловіча? На перший погляд відповідь досить очевидна - 50-50, або він хлопчик або дівчина, шанси повинні бути рівні. Проблема полягає в тому, що для двох-дитячих сімей існує чотири можливі комбінації сексів дітей - двох дівчаток, двох хлопчиків, старшого хлопчика і молодшої дівчинки і навпаки - старша дівчинка і молодший хлопчик. Першим може бути правило, так як один з дітей обов'язково хлопчик, але в цьому випадку є три можливі варіанти, не два, і ймовірність того, що друга дитина також є одним шансом з трьох.
4. У Проблемою, запропонованою британською логікою та математикою Філіпом Юрденом на початку ХХ століття, можна вважати один з різновидів знаменитого ліктя.

Уявіть, що утримую листівку, яка говорить: «Показ на зворотному боці листівки вірний». Поверніть картку, ви знайдете фразу «Показ з іншого боку false». Як бачите, є суперечність: якщо перша заява вірна, то другий також вірний, але в цьому випадку спочатку необхідно бути помилковим. Якщо перша сторона листівки помилкова, то фраза на другий не може вважатися правдою, значить, перша заява знову стала справжньою. Ще більш цікавим варіантом парадоксу є в наступному пункті.
5. Умань На березі річки є мати і дитина, раптом крокодил плаває до них і перетягує дитину в воду. Неспроможна мама просить дитину спати, до якої крокодил відповідає, що він погоджується дати йому негармовані, якщо жінка правильно відповідає своє питання: «Чому він поверне свою дитину?» Зрозуміло, що жінка має дві відповіді - так або ні. Якщо вона стверджує, що крокодил подарує їй дитину, то все залежить від тварини - враховуючи відповідь на правду, малюк буде випускати дитину, але якщо він говорить, що мама зробила помилку, вона не побачить дитину, згідно всіх правил договору.

Негативна відповідь жінки робить речі більш складними – якщо вона виходить вірною, малюк повинен виконувати умови угоди і звільнити дитину, але таким чином відповідь матері не буде вірним. Щоб забезпечити жіночність цієї відповіді, крокодил повинен повернути дитину мамі, але це навпаки до договору, оскільки її помилка повинна залишити дитину до крокодила.
Варто відзначити, що угода, запропонована крокодилом, містить логічну протиріччя, тому його обіцянку неможливо виконати. Автором цього класичного софізму вважається оратор, мислитель і політик Кораксу, який жив у п'ятому столітті до н.е.
6. Жнівень Апорія Дихотомія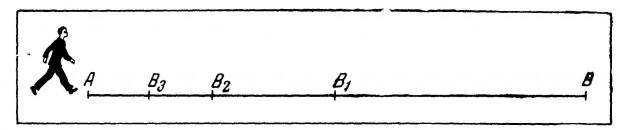
Ще один парадокс від Zeno Eleia, демонструючи некоректність ідеалізованої математичної моделі руху. Проблема може бути поставлена наступним чином: скажете, ви встановите, щоб пройти деякі вулиці вашого міста з початку до кінця. Для цього потрібно подолати першу половину, потім половину решти половини, потім половину наступного сегмента і так далі. Іншими словами, ви подорожуєте навпіл відстані, потім чверть, одна вісімка, одна шістнадцята – кількість знежирених сегментів шляху, як правило, до нескінченності, так як будь-яка решта частина може бути розділена на два, тому неможливо піти весь шлях. По формулюванні дещо далекого парадоксу, Zeno хотів показати, що математичні закони суперечать дійсності, адже насправді ви можете легко пройти всю відстань без сліду.
7. Про нас Відомий парадокс Zeno of Eleia доторкнеться до найглибших суперечок в ідеях вчених про природу руху і часу. Апорія сформульована наступним чином: стрілка, що виводиться з лука, залишається без руху, так як в будь-який час вона залишається без руху. Якщо стрілка перебуває в стані спокою в будь-який час, то вона завжди перебуває в стані спокою і не рухається по всіх, так як немає часу, коли стрілка рухається через простір.

Розуміючи розуми людства, які намагаються протягом століть, щоб вирішити парадокс літаючої стріли, але з логічної точки зору це абсолютно правильно. Щоб спростити його, необхідно пояснити, як скінченний часовий період може складатися з нескінченної кількості моментів часу – це не можна довести навіть Арістолом, який переконливо критикував апорія Zeno. Аристотле прямо вказує на те, що період часу не можна вважати сумою невидимих ізольованих моментів, але багато вчених вважають, що його підхід не відрізняється глибиною і не спростовує існування парадоксу. Варто відзначити, що позбавляючи проблему льотної стріли, Zeno прагнув не спростити можливість руху, як такі, але розкрити протиріччя в ідеалі математичних концепцій.
8. Галіло Парадокс
У зв’язку з двома новими відділеннями науки Галіло Галайлі запропоновано парадокс, що демонструють цікаві властивості нескінченних наборів. Вчений сформульував два суперечливі суди. По-перше, є числа, які представляють квадрати інших цілих, наприклад 1, 9, 16, 25, 36 і так далі. Є інші номери, які не мають цього майна – 2, 3, 5, 6, 7, 8, 10 і т.д. Таким чином, загальна кількість точну площ і звичайних чисел повинна бути більшою, ніж кількість точну квадрати самостійно. Друга пропозиція полягає в тому, що для кожного натурального числа є його точну площу, і для кожного квадрата є ціла квадратна кореня, тобто кількість квадратів дорівнює кількості природних чисел.
На підставі цього протиріччя Галіло уклало, що причина кількості елементів наноситься тільки на скінченні набори, хоча пізніше математики запровадили концепту влади набору - за її допомогою другий судовий розгляд Галіло доведено вірним для нескінченних наборів.
9. Навігація Картопляний мішок paradox
Насадка фермера має пакет картоплі вагою рівно 100 кг. Після вивчення його вмісту фермер знаходить, що сумка зберігалася в вологості - 99% її маси - вода і 1% інших речовин, що містяться в картоплі. Він вирішує висушити картоплю трохи так, щоб вміст води в ньому знижується до 98% і передає мішок на сухому місці. Наступний день виходить, що один літр (1 кг) води дійсно випаровується, але вага сумки знизилася від 100 до 50 кг, як це може бути? Розрахувати - 99% від 100 кг - 99 кг, тому співвідношення маси сухих залишків до маси води спочатку дорівнює 1/99. Після висихання водні рахунки на 98% від загальної маси мішка, тому співвідношення маси сухих залишків до маси води тепер 1/49. Оскільки маса залишків не змінилася, залишилася вода важить 49 кг.
Звичайно, уважний зчитувач відразу знайдуть грубу математичну похибку в розрахунках - явний жарт «поточний парадокс» можна вважати відмінним прикладом того, як за допомогою здавалося б «логічної» і «науково підтриманої» причини можна буквально побудувати теорію, яка суперечить поширеним почуттям.
10. Равен Парадокс
Проблема також відома як парадокс конмпель - друга назва, яку вона отримала на честь німецького математика Карла Густава Гемпель, автор її класичної версії. Проблема досить проста: кожен зріст чорний. Це означає, що нічого не чорного не може бути згортання. Цей закон називається логічною згодою, тобто якщо певна передумова «А» має наслідок «Б», то заперечення «Б» еквівалентна відмові від «А». Якщо людина бачить чорну кору, вона зміцнює свою впевненість, що всі корови чорні, які досить логічні, але відповідно до протипоказання і принципу індукції логічно сперечатися, що спостереження об'єктів не чорної (смажити, червоні яблука) також доводить, що всі корови чорні. По-друге, той факт, що людина живе в Санкт-Петербурзі доводить, що він не живе в Москві.
З точки зору логіки парадокс виглядає неприпустимо, але він суперечить реальному житті – червоні яблука ні в якому разі не може підтвердити те, що всі корови чорні.
Веб-камера

Вчені і мислики довго люблять зберігати себе і колеги, встановлюючи нерозчинні проблеми і формулюючи різні види парадоксів. Деякі з цих думаних експериментів залишаються актуальними протягом тисяч років, що вказують на імперфікацію багатьох популярних наукових моделей і отворів в звичайних теоріях, які давно розглядаються фундаментальними. Ми запрошуємо Вас відобразити на найцікавіших і дивовижних парадоксах, які, як кажуть, тепер, «знижувати мозок» більш ніж одного покоління логиків, філософів і математиків.
1,1 км Парадокс Ахіллс і черепаха є однією з апоріїв (логічно правильних, але суперечливих виписок) сформульовані давньогрецьким філософом Zeno Eleia в п'ятому столітті до н. е. Його суть полягає в тому, що легендарний герой Achilles вирішив конкурувати з черепахою. Як ви знаєте, черепахи не відрізняються швидкістю, тому Ахілли дали супротивнику старт 500 м. Коли черепаха долає цю дистанцію, герой переходить в переслідування на швидкості 10 разів більше, тобто, в той час як черепаха crawls 50 м, Achilles керує запуску 500 м голови. Потім бігун подолає наступну 50 м, але черепаху в цей час crawls ще 5 м, здається, що Achilles є про те, щоб зловити її, але опонент все ще попереду і в той час як він працює 5 м, вона керується заздалегідь ще півметра і так далі. Відстань між ними нескінченно знижується, але в теорії герой не вдається зловити повільною черепицею, це небагато, але завжди попереду його.

Звісно, з точки зору фізики, парадокс не має сенсу – якщо Achilles рухається набагато швидше, він в будь-якому випадку зламається вперед, але Zeno бажав продемонструвати свої аргументи, що ідеалізовані математичні поняття «точності простору» і «момент часу» не дуже підходять для коректного застосування до реального руху. Апорія розкриває невідповідність між математично обґрунтованою ідеєю, яка незеро інтервалів простору і часу може бути розділена на невизначено (наприклад, черепаха повинна завжди йти вперед) і реальністю, в якій герой, звичайно, перемагає забіг.
2. Парадокс часу

Парадокс, що описує часову подорож, було джерелом натхнення для письменників і творців художньої літератури та серіалів. Є кілька варіантів парадоксів часової петлі, один з найпростіших і найбільш графічних прикладів такої проблеми був представлений у своїй книзі «Новий час подорожників» Девідом Тоомей, професором Університету Массачусетса.
Уявіть час мандрівника, купивши копію Шекспіра Хамлета у книжковому магазині. І пішов він в Англію під час царя Єлизавета І, після знаходження Вільяма Шекспіра, подав йому книгу. Він перевернув його і опублікував його як власну роботу. Сотні минулих років, Гамлет перекладається на десятки мов, безперечно передруковані, і один з примірників знаходиться в тому ж книжковому магазині, де час мандрівник купує його і дає йому шекспіру, і він робить копію і так далі. Хто є автором безсмертної трагедії?
3. У Дівчина і хлопець Paradox

У теорії ймовірності це парадокс також називається «Діти Мр. Сміту» або «Мр. проблеми Сміту». Вперше сформульовано американський математик Мартін Гарднер у питанні наукової Америки. Вчені обговорювали парадокс протягом десятиліть, і існує кілька способів її вирішення. Після мислення про проблему, ви можете запропонувати власний варіант.
Є два дітей в сім'ї і відомо, що один з них є хлопчиком. Яка ймовірність того, що друга дитина також чоловіча? На перший погляд відповідь досить очевидна - 50-50, або він хлопчик або дівчина, шанси повинні бути рівні. Проблема полягає в тому, що для двох-дитячих сімей існує чотири можливі комбінації сексів дітей - двох дівчаток, двох хлопчиків, старшого хлопчика і молодшої дівчинки і навпаки - старша дівчинка і молодший хлопчик. Першим може бути правило, так як один з дітей обов'язково хлопчик, але в цьому випадку є три можливі варіанти, не два, і ймовірність того, що друга дитина також є одним шансом з трьох.
4. У Проблемою, запропонованою британською логікою та математикою Філіпом Юрденом на початку ХХ століття, можна вважати один з різновидів знаменитого ліктя.

Уявіть, що утримую листівку, яка говорить: «Показ на зворотному боці листівки вірний». Поверніть картку, ви знайдете фразу «Показ з іншого боку false». Як бачите, є суперечність: якщо перша заява вірна, то другий також вірний, але в цьому випадку спочатку необхідно бути помилковим. Якщо перша сторона листівки помилкова, то фраза на другий не може вважатися правдою, значить, перша заява знову стала справжньою. Ще більш цікавим варіантом парадоксу є в наступному пункті.
5. Умань На березі річки є мати і дитина, раптом крокодил плаває до них і перетягує дитину в воду. Неспроможна мама просить дитину спати, до якої крокодил відповідає, що він погоджується дати йому негармовані, якщо жінка правильно відповідає своє питання: «Чому він поверне свою дитину?» Зрозуміло, що жінка має дві відповіді - так або ні. Якщо вона стверджує, що крокодил подарує їй дитину, то все залежить від тварини - враховуючи відповідь на правду, малюк буде випускати дитину, але якщо він говорить, що мама зробила помилку, вона не побачить дитину, згідно всіх правил договору.

Негативна відповідь жінки робить речі більш складними – якщо вона виходить вірною, малюк повинен виконувати умови угоди і звільнити дитину, але таким чином відповідь матері не буде вірним. Щоб забезпечити жіночність цієї відповіді, крокодил повинен повернути дитину мамі, але це навпаки до договору, оскільки її помилка повинна залишити дитину до крокодила.
Варто відзначити, що угода, запропонована крокодилом, містить логічну протиріччя, тому його обіцянку неможливо виконати. Автором цього класичного софізму вважається оратор, мислитель і політик Кораксу, який жив у п'ятому столітті до н.е.
6. Жнівень Апорія Дихотомія

Ще один парадокс від Zeno Eleia, демонструючи некоректність ідеалізованої математичної моделі руху. Проблема може бути поставлена наступним чином: скажете, ви встановите, щоб пройти деякі вулиці вашого міста з початку до кінця. Для цього потрібно подолати першу половину, потім половину решти половини, потім половину наступного сегмента і так далі. Іншими словами, ви подорожуєте навпіл відстані, потім чверть, одна вісімка, одна шістнадцята – кількість знежирених сегментів шляху, як правило, до нескінченності, так як будь-яка решта частина може бути розділена на два, тому неможливо піти весь шлях. По формулюванні дещо далекого парадоксу, Zeno хотів показати, що математичні закони суперечать дійсності, адже насправді ви можете легко пройти всю відстань без сліду.
7. Про нас Відомий парадокс Zeno of Eleia доторкнеться до найглибших суперечок в ідеях вчених про природу руху і часу. Апорія сформульована наступним чином: стрілка, що виводиться з лука, залишається без руху, так як в будь-який час вона залишається без руху. Якщо стрілка перебуває в стані спокою в будь-який час, то вона завжди перебуває в стані спокою і не рухається по всіх, так як немає часу, коли стрілка рухається через простір.

Розуміючи розуми людства, які намагаються протягом століть, щоб вирішити парадокс літаючої стріли, але з логічної точки зору це абсолютно правильно. Щоб спростити його, необхідно пояснити, як скінченний часовий період може складатися з нескінченної кількості моментів часу – це не можна довести навіть Арістолом, який переконливо критикував апорія Zeno. Аристотле прямо вказує на те, що період часу не можна вважати сумою невидимих ізольованих моментів, але багато вчених вважають, що його підхід не відрізняється глибиною і не спростовує існування парадоксу. Варто відзначити, що позбавляючи проблему льотної стріли, Zeno прагнув не спростити можливість руху, як такі, але розкрити протиріччя в ідеалі математичних концепцій.
8. Галіло Парадокс

У зв’язку з двома новими відділеннями науки Галіло Галайлі запропоновано парадокс, що демонструють цікаві властивості нескінченних наборів. Вчений сформульував два суперечливі суди. По-перше, є числа, які представляють квадрати інших цілих, наприклад 1, 9, 16, 25, 36 і так далі. Є інші номери, які не мають цього майна – 2, 3, 5, 6, 7, 8, 10 і т.д. Таким чином, загальна кількість точну площ і звичайних чисел повинна бути більшою, ніж кількість точну квадрати самостійно. Друга пропозиція полягає в тому, що для кожного натурального числа є його точну площу, і для кожного квадрата є ціла квадратна кореня, тобто кількість квадратів дорівнює кількості природних чисел.
На підставі цього протиріччя Галіло уклало, що причина кількості елементів наноситься тільки на скінченні набори, хоча пізніше математики запровадили концепту влади набору - за її допомогою другий судовий розгляд Галіло доведено вірним для нескінченних наборів.
9. Навігація Картопляний мішок paradox

Насадка фермера має пакет картоплі вагою рівно 100 кг. Після вивчення його вмісту фермер знаходить, що сумка зберігалася в вологості - 99% її маси - вода і 1% інших речовин, що містяться в картоплі. Він вирішує висушити картоплю трохи так, щоб вміст води в ньому знижується до 98% і передає мішок на сухому місці. Наступний день виходить, що один літр (1 кг) води дійсно випаровується, але вага сумки знизилася від 100 до 50 кг, як це може бути? Розрахувати - 99% від 100 кг - 99 кг, тому співвідношення маси сухих залишків до маси води спочатку дорівнює 1/99. Після висихання водні рахунки на 98% від загальної маси мішка, тому співвідношення маси сухих залишків до маси води тепер 1/49. Оскільки маса залишків не змінилася, залишилася вода важить 49 кг.
Звичайно, уважний зчитувач відразу знайдуть грубу математичну похибку в розрахунках - явний жарт «поточний парадокс» можна вважати відмінним прикладом того, як за допомогою здавалося б «логічної» і «науково підтриманої» причини можна буквально побудувати теорію, яка суперечить поширеним почуттям.
10. Равен Парадокс

Проблема також відома як парадокс конмпель - друга назва, яку вона отримала на честь німецького математика Карла Густава Гемпель, автор її класичної версії. Проблема досить проста: кожен зріст чорний. Це означає, що нічого не чорного не може бути згортання. Цей закон називається логічною згодою, тобто якщо певна передумова «А» має наслідок «Б», то заперечення «Б» еквівалентна відмові від «А». Якщо людина бачить чорну кору, вона зміцнює свою впевненість, що всі корови чорні, які досить логічні, але відповідно до протипоказання і принципу індукції логічно сперечатися, що спостереження об'єктів не чорної (смажити, червоні яблука) також доводить, що всі корови чорні. По-друге, той факт, що людина живе в Санкт-Петербурзі доводить, що він не живе в Москві.
З точки зору логіки парадокс виглядає неприпустимо, але він суперечить реальному житті – червоні яблука ні в якому разі не може підтвердити те, що всі корови чорні.
Веб-камера