659
«Добрі батьки виростають з бідних дітей»: 5 смішних наукових парадоксів
Чи є хто хоче бути красивим конем? . Кожен любить красиву коню, але ніхто не хоче бути. З кожним поколінням діти стають гіршими і батьками краще, звідси, від самих маленьких дітей краще ростуть і краще батьків. Список парадоксів є нескінченним – ми будемо говорити тільки про найцікавіші з них.

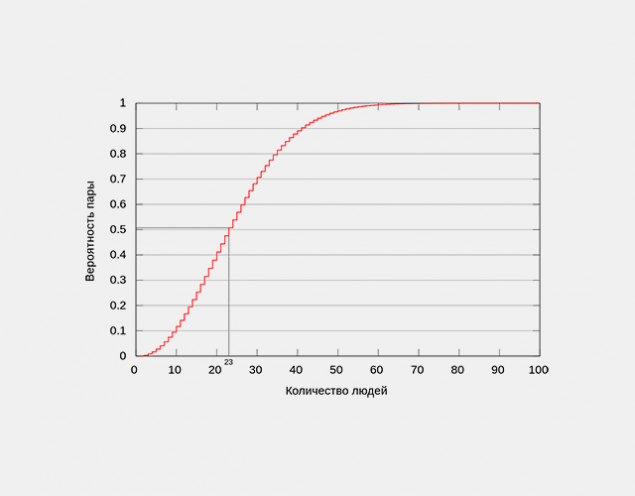
Ця заява стверджує, що в групі 23 або більше осіб, ймовірність, що принаймні два з них будуть мати однаковий день народження (номер і місяць) перевищує 50%. Для 60 або більше людей ця ймовірність перевищує 99%, але 100%, відповідно до так званого принципу Dirichlet, досягне лише тоді, коли в групі не менше 367 осіб.
Ця заява не може здатися очевидною, оскільки ймовірність збігу з дня народження для двох осіб в будь-який день року (1/365 = 0,27%), переповнена кількістю людей в групі 23 учасників, дає лише 23/365 = 6.3%. Тим не менш, ця причина неправильна, так як кількість можливих пар (253) набагато більше кількості людей в групі. Таким чином, заява не може вважатися строго науковими парадоксами: в ній немає логічної суперечності, а парадокс знаходиться лише в відмінності між інтуїтивно зрозумілим сприйняттям таких обставин людиною і результатами математичних обчислень.
Ліар Парадокс - це заява «Що я кажу зараз помилково». Заява суперечить одному з фундаментальних принципів класичної математики - закону виключеної третини (складається з того, що з двох виписок - "А" і "не", А" - одна обов'язково помилкова, а друга - вірна, тобто обидві заяви не можуть бути одночасно помилковими - NS).
Припустимо, що ця заява є вірною, потім, на основі її змісту, це також правда, що це також помилково. Але якщо це помилково, то що це говорить помилково. Тому не вірно, що ця заява є брехливою. Так твердження вірно. Так ми повертаємося до початку аргументу.
У своїй структурі Софія нагадує парадокс ліри. Автор парадоксу – древній грецький оратор Коракс. Це формулювання парадоксу. А крокодил кинув дитину з єгипетської жінки, що стоїть на річці. Коли попросили повернути дитину, крокодил відповів, "Я даю вам шанс отримати його назад, але ви повинні вгадати, що я даю вам або ні." Якщо ви відповіли правильно, я даю дитину, ні, не буду тримати його. "Ви не дадуть мені дитину." "Я не буду," відповів крокодил, "Що ви сказали, що правда або ви лікували." Якщо те, що я не даю дитину вірним, я не даю йому, бо інакше що говорить не буде вірним. Якщо що це не вірно, то ви не вгадали, і я не дам дитину за домовленістю. (Українська) «Дякую за те, що я скажу правду, ви подаруєте мені дитину, як ми домовилися». Якщо я не здогадував, що ви не дасте дитину, то ви повинні дати мені, інакше що я сказав, що не буде неправдивим. Хто правий, мати або крокодил?
Обіцяти крокодила властиво суперечливості, а отже не можна виконати на підставі законів логіки.
Парадокс Куррі "Якщо ця заява є справжньою, то існують рмади," читайте цю заяву. Давайте спробуємо розпустити його. Скажимо "А." Якщо "А" вірно, то існують мериди. Але ми не знаємо, якщо "А" правда. Якщо А були вірними, це означатиме існування русалки. Але це те, що «А» говорить, що «А» це право. Хенце, русалки існують.
Причиною приготовленого парадоксу є використання самореференції в заяві, що неприпустимо.
І це парадокс, який ми повинні мати справу з усього часу. Більша теорія фольги може бути викликана теорія ММММ. Вона стверджує, що це можливо зробити гроші на будь-які цінні папери, незалежно від їх вартості, перш за все, купуючи їх, а потім продаючи їх на прибуток, тому що завжди є хтось павутин ("великий фольг"), який також очікує, щоб швидко відновити актив на прибуток. На цьому принципі будуються спекулятивні бульбашки, які обов'язково лопаються, зводячи ціни на масовий ринок.
по голий-science.ru/article/top/nauchnye-paradoksy

Ця заява стверджує, що в групі 23 або більше осіб, ймовірність, що принаймні два з них будуть мати однаковий день народження (номер і місяць) перевищує 50%. Для 60 або більше людей ця ймовірність перевищує 99%, але 100%, відповідно до так званого принципу Dirichlet, досягне лише тоді, коли в групі не менше 367 осіб.
Ця заява не може здатися очевидною, оскільки ймовірність збігу з дня народження для двох осіб в будь-який день року (1/365 = 0,27%), переповнена кількістю людей в групі 23 учасників, дає лише 23/365 = 6.3%. Тим не менш, ця причина неправильна, так як кількість можливих пар (253) набагато більше кількості людей в групі. Таким чином, заява не може вважатися строго науковими парадоксами: в ній немає логічної суперечності, а парадокс знаходиться лише в відмінності між інтуїтивно зрозумілим сприйняттям таких обставин людиною і результатами математичних обчислень.

Ліар Парадокс - це заява «Що я кажу зараз помилково». Заява суперечить одному з фундаментальних принципів класичної математики - закону виключеної третини (складається з того, що з двох виписок - "А" і "не", А" - одна обов'язково помилкова, а друга - вірна, тобто обидві заяви не можуть бути одночасно помилковими - NS).
Припустимо, що ця заява є вірною, потім, на основі її змісту, це також правда, що це також помилково. Але якщо це помилково, то що це говорить помилково. Тому не вірно, що ця заява є брехливою. Так твердження вірно. Так ми повертаємося до початку аргументу.
У своїй структурі Софія нагадує парадокс ліри. Автор парадоксу – древній грецький оратор Коракс. Це формулювання парадоксу. А крокодил кинув дитину з єгипетської жінки, що стоїть на річці. Коли попросили повернути дитину, крокодил відповів, "Я даю вам шанс отримати його назад, але ви повинні вгадати, що я даю вам або ні." Якщо ви відповіли правильно, я даю дитину, ні, не буду тримати його. "Ви не дадуть мені дитину." "Я не буду," відповів крокодил, "Що ви сказали, що правда або ви лікували." Якщо те, що я не даю дитину вірним, я не даю йому, бо інакше що говорить не буде вірним. Якщо що це не вірно, то ви не вгадали, і я не дам дитину за домовленістю. (Українська) «Дякую за те, що я скажу правду, ви подаруєте мені дитину, як ми домовилися». Якщо я не здогадував, що ви не дасте дитину, то ви повинні дати мені, інакше що я сказав, що не буде неправдивим. Хто правий, мати або крокодил?
Обіцяти крокодила властиво суперечливості, а отже не можна виконати на підставі законів логіки.
Парадокс Куррі "Якщо ця заява є справжньою, то існують рмади," читайте цю заяву. Давайте спробуємо розпустити його. Скажимо "А." Якщо "А" вірно, то існують мериди. Але ми не знаємо, якщо "А" правда. Якщо А були вірними, це означатиме існування русалки. Але це те, що «А» говорить, що «А» це право. Хенце, русалки існують.
Причиною приготовленого парадоксу є використання самореференції в заяві, що неприпустимо.
І це парадокс, який ми повинні мати справу з усього часу. Більша теорія фольги може бути викликана теорія ММММ. Вона стверджує, що це можливо зробити гроші на будь-які цінні папери, незалежно від їх вартості, перш за все, купуючи їх, а потім продаючи їх на прибуток, тому що завжди є хтось павутин ("великий фольг"), який також очікує, щоб швидко відновити актив на прибуток. На цьому принципі будуються спекулятивні бульбашки, які обов'язково лопаються, зводячи ціни на масовий ринок.
по голий-science.ru/article/top/nauchnye-paradoksy