10 paradojas lógicas entretenimiento Bashny.Net

Si después de leer esta colección, no te equivocas por completo, por lo que creo lo suficientemente
yasno


Los estudiosos y pensadores de la antigüedad encanta entretenerse y sus colegas de estadificación problemas sin solución y la formulación de diversos tipos de paradojas. Algunos de estos experimentos mentales siguen siendo pertinentes durante miles de años, lo que indica que la imperfección de muchos modelos de divulgación científica y de "agujeros" en las teorías generalmente aceptadas, siempre se ha considerado fundamental. Te invitamos a reflexionar sobre la paradoja más interesante y sorprendente que, como ahora se expresó, "hizo estallar el cerebro" a las generaciones de lógicos, filósofos y matemáticos.

1. aporía "Aquiles y la tortuga" paradoja de Aquiles y la tortuga - una de las paradojas (lógicamente declaraciones verdaderas pero contradictorias), formuladas por el filósofo griego Zenón de Elea en el siglo V-IV aC. Su esencia es la siguiente: el legendario héroe de Aquiles decidió competir en la carrera con una tortuga. Como usted sabe, las tortugas no difieren prytkost, por lo que Aquiles dio a su oponente una ventaja en los 500 metros. Cuando la tortuga supera esta distancia, el héroe se embarca en una proporción de 10 veces mayor, es decir, hasta que el animal se arrastra 50 metros, Aquiles tiene tiempo para correr los datos que 500m probabilidades . Entonces el corredor supera los próximos 50 metros, pero la tortuga en este momento se arrastra por otro 5 m, parece que Aquiles era sobre él se pondrá al día, pero el adversario está aún por llegar, y hasta que se corre 5 metros, se las arregla para pasar por otro medio metro, y así sucesivamente. La distancia entre ellos es infinitamente reducido, pero en teoría, el héroe no logró alcanzar a la tortuga lenta, no es mucho, pero siempre por delante de él
.


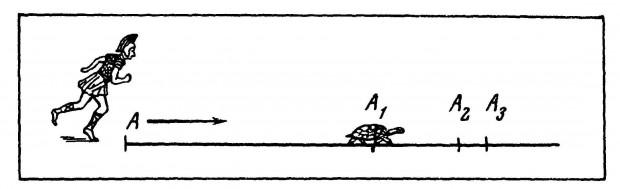
Por supuesto, desde el punto de vista de la paradoja de la física no tiene sentido - si Aquiles está moviendo mucho más rápido en todo caso va a romper hacia adelante, pero Zenón, en primer lugar, quería mostrar sus argumentos de que los conceptos matemáticos idealizados "punto en el espacio" y "punto en el tiempo" no es muy apropiado para la correcta aplicación del movimiento real. Aporía revela una discrepancia entre la matemática justificada por la idea de que los intervalos no cero de espacio y tiempo se pueden dividir infinitamente (por lo que la tortuga siempre debe mantenerse por delante) y la realidad en la que el héroe, por supuesto, gana la carrera.

2. La paradoja del tiempo petli

Paradojas que describen los viajes en el tiempo, durante mucho tiempo una fuente de inspiración para escritores y creadores de películas de ciencia ficción y series de televisión de ciencia ficción. Hay varias variantes de las paradojas del bucle de tiempo, uno de los ejemplos más simples y evidentes de este tipo de problemas se tradujo en su libro «The New Time Travelers» («New Time Traveler") David Toomey, profesor en la Universidad de Massachusetts.

Imagínese lo que un viajero del tiempo había comprado en una librería un ejemplar de Shakespeare "Hamlet". A continuación, pasó a Inglaterra, el tiempo de la reina Isabel I, la Virgen y buscar William Shakespeare, le hizo entrega de un libro. Él volvió a escribir y publicó como suyo. Pase por cientos de años, "Hamlet" es traducido a decenas de idiomas, sin parar la reproducción, y una copia se encuentra en la misma librería, donde un viajero del tiempo lo compra y le da Shakespeare, y se ocupa, y así sucesivamente ... ¿Quién en este caso se debe considerar autor de la tragedia inmortal?

3. La paradoja de las niñas y malchika

En teoría de la probabilidad, la paradoja es también llamado el "Children of Mr. Smith" o "señora Smith problema". Fue formulado por primera vez por el matemático estadounidense Martin Gardner en una de las habitaciones de la revista «Scientific American». Los científicos discuten sobre la paradoja durante décadas, y hay varias maneras de su resolución. Después de pensar en el problema, y ​​usted puede ofrecer su propia versión.

La familia tiene dos hijos, y se sabe que uno de ellos - un niño. ¿Cuál es la probabilidad de que el segundo hijo también tiene sexo masculino? A primera vista, la respuesta es obvia - 50 de 50, o en realidad un niño o una niña, las probabilidades que ser iguales. El problema es que para las familias con dos niños hay cuatro combinaciones posibles de los niños sexos - dos niñas, dos niños, el niño mayor y la niña y viceversa más joven - una chica y un chico mayor más jóvenes. El primero puede ser eliminado, ya que uno de los niños exactamente el chico, pero en este caso son tres opciones en lugar de dos, y la probabilidad de que el segundo hijo también es un muchacho -. Una posibilidad de tres

4. La paradoja Jourdain con kartochkoyProblemu propuesto por el matemático británico y lógico Philippe Jourdain al principio del XX-XX siglo, se puede considerar una variación de la famosa paradoja del mentiroso.



Imagínese - usted está sosteniendo una tarjeta que dice: "La aprobación de la parte posterior de la tarjeta es cierto." Encendido de la tarjeta, se dará cuenta de la frase "La declaración es falsa en el otro lado." Como se puede imaginar, hay una contradicción si la primera afirmación verdadera, la segunda también es cierto, pero en este caso, la primera debe ser falsa. Si la primera tarjeta del partido es falsa, entonces la segunda frase no puede ser considerado como verdadero, lo que significa que la primera declaración de nuevo se convierte en la verdad ... Incluso la versión más interesante de la paradoja del mentiroso -. En el párrafo siguiente

5. sofisma "Cocodrilo", a orillas del río son una madre con un niño, de repente un cocodrilo nada para él y saca al niño en el agua. Inconsolable madre le pide que devuelva el niño, lo que el cocodrilo dice que está de acuerdo para darle ileso, si una mujer la respuesta correcta a la pregunta: "¿El regreso del niño si lo hizo". Está claro que las mujeres son dos respuestas - sí o no. Si ella sostiene que el cocodrilo le daría un hijo, todo depende de que el animal - teniendo en cuenta la verdadera respuesta ladrón soltó el niño, si él dice que su madre estaba mal, que no vio al niño, de acuerdo con las normas del tratado
.


Una respuesta negativa a una mujer complica considerablemente todo - si bien es cierto, el ladrón debe cumplir con los términos de la transacción y la liberación del niño, pero la madre para que la respuesta no corresponde a la realidad. Para asegurarse de que la falsedad de tal respuesta, el cocodrilo es necesario devolver el niño a la madre, pero esto contradice el acuerdo porque su error debe dejar al niño de un cocodrilo.

Vale la pena señalar que el acuerdo propuesto por el cocodrilo, contiene una contradicción lógica, por lo que su promesa imposible. El autor de este sofisma clásica considerado altavoz, pensador y político Corax de Syracuse, que vivió en el siglo I aC-V º.

6. aporía "Dicotomía"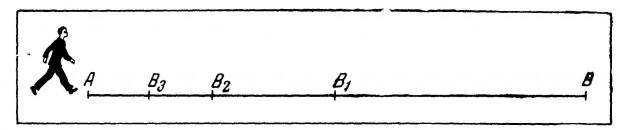

Otra paradoja de Zenón de Elea, mostrando incorrecta modelo matemático idealizado de movimiento. El problema se puede poner de esta manera - digamos que se dispuso a pasar por algunas calles de tu ciudad desde el principio hasta el final. Para ello, tiene que superar su primera mitad, luego la mitad de la mitad restante, entonces la mitad del segmento siguiente, y así sucesivamente. En otras palabras - usted pasa por la mitad de la distancia, a continuación, un cuarto, un octavo, un dieciseisavo - disminuyendo el número de segmentos de la ruta de acceso tiende a infinito, ya que cualquier parte restante se puede dividir en dos partes, a continuación, ir hasta el final del todo imposible. Dicho de un tanto inverosímil, a primera vista paradójico, Zenón quiso demostrar que las leyes matemáticas son contrarias a la realidad, porque en realidad se puede pasar fácilmente todo por la borda sin dejar rastro.

7. aporía "Flying Arrow" La famosa paradoja de Zenón de Elea toca las contradicciones más profundas en las opiniones de los científicos sobre la naturaleza del tiempo y el movimiento. Aporía formulado como: una flecha disparada con un arco, que permanece inmóvil, como en cualquier momento está en reposo, sin hacer movimiento. No Si en cualquier momento el resto de la flecha, entonces es siempre en un estado de reposo y se mueve en absoluto, ya que hay un momento en el que que la pluma en el espacio.



Mentes sobresalientes de la humanidad por siglos tratando de resolver la paradoja de la flecha volar, pero desde un punto de vista lógico, que se hace absolutamente cierto. Por su refutación se requiere para explicar cómo el intervalo de tiempo finito puede consistir en un número infinito de veces - para demostrar que no era posible, incluso a Aristóteles, criticado duramente Zeno. Aristóteles señaló acertadamente que la longitud de tiempo que no puede ser considerada como una suma de algunos momentos aislados indivisibles, pero muchos científicos creen que su enfoque es diferente profundidad y no niega la existencia de una paradoja. Cabe señalar que la formulación del problema flecha volar Zeno no buscaba negar la posibilidad de movimiento, como tal, sino para revelar las contradicciones en los conceptos matemáticos idealistas.

8. La paradoja Galileya

En sus "Conversaciones y demostraciones matemáticas en relación con dos nuevas ramas de la ciencia" obra Galileo Galilei propuso una paradoja que muestran interesantes propiedades de los conjuntos infinitos. El científico formuló dos sentencias contradictorias. En primer lugar, hay números que representan los otros cuadrados de números enteros, tales como 1, 9, 16, 25, 36 y así sucesivamente. Hay otros números que no tienen esta propiedad - 2, 3, 5, 6, 7, 8, 10, y similares. Así, el número total exacto de cuadrados y los números habituales para ser más preciso que el número de plazas sólo. La segunda proposición: para todo entero positivo existe una cuadratura exacta, y cada plaza hay una raíz cuadrada, es decir, el número de casillas igual al número de enteros positivos
.
Sobre la base de esta contradicción, Galileo llegó a la conclusión de que los argumentos sobre el número de elementos aplicados sólo para conjuntos finitos, aunque los matemáticos posteriores introdujeron el concepto, el poder del conjunto - con que se ha demostrado lealtad al segundo juicio de Galileo y de los conjuntos infinitos
.
9. La bolsa paradoja kartofelya

Digamos que un determinado agricultor tiene un saco de patatas que pesan exactamente 100 kg. Después de examinar su contenido, un campesino descubre que la bolsa se mantiene en la humedad - 99% de su peso es agua, y 1% de otras sustancias contenidas en las patatas. Resuelve patatas bits seca, el contenido de agua en el que disminuyó en un 98% y transporta la bolsa en un lugar seco. Al día siguiente, resulta que un litro (1 kg) de agua en realidad se evapora, pero el peso de la bolsa cayó de 100 a 50 kg, ¿cómo puede ser esto? Vamos a contar - el 99% de 100 kg es de 99 kg, entonces la relación en peso de residuo seco y la masa de agua inicialmente igual a 1/99. Después del secado, el agua comprende 98% del peso total de la bolsa, por lo que la relación de la masa seca del residuo al peso de agua es ahora 1/49. Dado que el balance de masa no ha cambiado, el agua restante pesa 49 kg.

Por supuesto, el lector atento detectará de inmediato un error matemático bruto en el cálculo - un cómic "saco paradoja de patatas" imaginario puede ser considerado un excelente ejemplo de cómo utilizar el aparentemente "lógica" y "científicamente respaldado por" razonamiento puede literalmente desde cero para construir una teoría contraria a la común lo que significa.

10. El voronov
paradoja
El problema también se conoce como la paradoja de Hempel - el segundo nombre que recibió en honor al matemático alemán Carl Hempel, el autor de su versión clásica. El problema se formula muy simple: cada cuervo es negro. De ello resulta que todo lo que no es negro, no ser un cuervo. Esta ley es una contraposición lógica, es decir, si una determinada parcela "A" es el resultado de "B", la negación de la "B" equivale a negar la "A". Si una persona ve un cuervo negro, que refuerza su creencia de que todos los cuervos son de color negro, lo cual tiene sentido, pero de acuerdo con la contraposición y el principio de inducción lógicamente argumentar que la observación de objetos no negras (por ejemplo, manzanas rojas) también demuestra que todos los cuervos son de color negro. En otras palabras - que la persona que vive en San Petersburgo que pruebe que él no vive en Moscú
.
Desde el punto de vista de la paradoja lógica se ve perfectamente, pero es contrario a la vida real - manzanas rojas no pueden de ninguna manera confirma el hecho de que todos los cuervos son negro
.
a través factroom.ru