828
10有趣的逻辑悖论
如果阅读本收集之后,你不要弄乱完全,所以你觉得够yasno
从远古时代的学者和思想家喜欢娱乐自己和同事分期无法解决的问题,并制定各种矛盾的。其中的一些思想实验仍然适用千百年来,这表明许多流行的科学模型中普遍接受的理论的不完善和“洞”,一直被认为是根本。我们邀请您反映最有趣,最令人惊讶的自相矛盾的,因为它是现在表示,“炸毁了大脑”来代逻辑学家,哲学家和数学家。
1.绢“阿基里斯与龟”阿基里斯悖论和龟 - 悖论(逻辑真,但矛盾的说法),通过埃利亚在V-世纪公元前古希腊哲学家芝诺制定之一。其实质是:传奇英雄阿喀琉斯决定与乌龟比赛竞争。如你所知,乌龟没有什么不同prytkost,所以阿喀琉斯送给了对手一个良好的开端,在500米,当乌龟克服了这个距离,主人公以10倍的速度衬托,也就是说,直到乌龟爬50米跟腱有时间运行数据也500米赔率。然后,亚军克服未来的50米,但乌龟在这个时候爬由另外5男,似乎阿基里斯它会赶上,但对手还是要来,直到它运行5米,她设法将另一半米,等等。它们之间的距离被无限缩小,但在理论上,英雄没能赶上低迷的乌龟,它不是太大,但总是在他的前面。
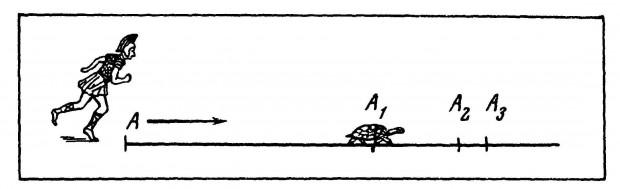
当然,从物理矛盾的一点是没有意义的 - 如果跟腱快得多移动在任何情况下,他将打破前锋,但芝诺,首先,想展示他的论点是理想化的数学概念“点空间”和“时间点”是不非常适合于实际运动的正确应用。绢揭示了数学上合理之间的差异的想法,非零间隔的时间和空间可以无限分割(所以龟必须始终保持领先地位),与现实中的主人公,当然,赢得了比赛。
2.上的说法petli
悖论描述时间旅行,时间长灵感科幻小说作家和科幻电影和电视剧的创作者的来源。有时间循环的悖论几个变种,对这些问题的最简单而明显的例子之一造成的在他的著作«新的时间旅行者»(«新的时间旅行者“)大卫·图梅,马萨诸塞大学的教授。
想象一下,一个时间旅行者在书店买了莎士比亚的副本,“哈姆雷特”。然后,他去了英国,女王伊丽莎白一世的时候,维尔京,寻找威廉·莎士比亚,送了他一本书。他改写了它,并出版了他自己的。经过了几百年,“哈姆雷特”被翻译成数十种语言,无休止地重现,而另一份是在同一个书店,其中一个时间旅行者购买它,并给莎士比亚,他占用了,等等...谁在这种情况下,应考虑不朽的悲剧作家?
3.女生的矛盾和malchika
在概率论,矛盾也被称为“儿童史密斯先生”或“女士斯密问题”。它最早是由美国数学家马丁·加德纳在该杂志«科学美国人»其中一个房间内制定。科学家们争论的悖论了几十年,并有决议的几种方法。经过思考这个问题,你可以提供你自己的版本。
这个家庭有两个孩子,已知其中之一 - 一个男孩。什么是第二个孩子也有男性的概率是多少?乍一看,答案是显而易见的 - 50的50,还是他真的是男孩还是女孩,胜算必须相等。问题是,对家庭有两个孩子有男女儿童的四种可能的组合 - 两个女孩,两个男孩,大男孩和最小的女孩,反之亦然 - 一个女孩和一个男孩年长年轻。第一个可以被消除,因为孩子们完全男孩之一,但在这种情况下有三个选项,而不是两个,且第二子也是男孩的概率 - 三分之一的机会
4.矛盾茹尔丹与kartochkoyProblemu在二十个世纪初提出的英国数学家和逻辑学家菲利普·茹尔丹,可以被认为是骗子的著名悖论的变化。

想象一下 - 你持有一张卡,上面写着:“批准该卡的背面是真实的。”打开卡,你会发现这句话“的说法是错误的另一面。”你可以想像,有一个矛盾,如果第一条语句真,第二个也是如此,但在这种情况下,第一个肯定是假的。如果第一方证是假的,那么第二句不能算是真正的,这意味着第一个语句重新成为真理......更有意思的说谎者悖论的版本 - 在未来的一段
5.诡辩“鳄鱼”在河岸边是一个母亲带着孩子,突然一只鳄鱼游到他和拉孩子在水中。伤心欲绝的母亲要求她还给孩子,什么鳄鱼说,他同意给它一劫,如果一个女人正确回答他的问题:“如果他的孩子的回报”。很显然,女性两个答案 - 是或否。如果她认为,鳄鱼会给她一个孩子,这一切都取决于动物 - 考虑到答案真正的小偷放过孩子,如果他说,他的母亲是错误的,她没看到孩子,根据条约的规定
。

对一个女人产生负响应相当复杂的一切 - 如果这是真的,小偷必须履行的交易的条款和释放孩子,但他的母亲,这样的回答并不符合现实。为了确保这种反应是虚假的,鳄鱼就要还给孩子的母亲,但这违背了协议,因为它的误差必须留下鳄鱼的孩子。
值得一提的是,提出鳄鱼的交易,蕴含着逻辑上的矛盾,所以他的承诺是不可能的。这个经典的诡辩的作者认为雪城,谁住在V世纪公元前扬声器,思想家,政治家CORAX。
6.绢“二分法”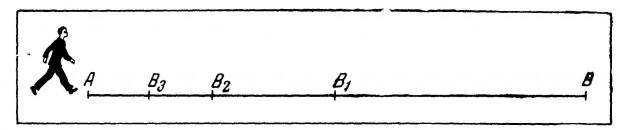
埃利亚的芝诺的悖论另外,表现出运动的不正确理想化的数学模型。这个问题可以把这种方式 - 让我们说你准备从开始到结束都要经过你的城市的一些街道。要做到这一点,你需要克服其前半,然后一半,剩下的一半,那么一半的下一个段的,依此类推。换句话说 - 你经过距离的一半,那么四分之一,八分之一,十六分之一 - 降低的路径段的数量趋于无穷,因为任何剩余部分可以分为两部分,然后一路完全不可能。换句话说乍一看矛盾有所牵强,芝诺想证明数学规律是违背现实的,因为事实上,你可以很容易地通过所有走的无影无踪。
7.绢“飞矢”埃利亚的芝诺的悖论著名触动最深的矛盾有关的时间和运动性科学家的意见。绢公式表示为:从弓的箭射击,它仍然是固定的,因为在任何时候它是静止的,未做举动。如果在任何时候箭头静止状态,那么它总是在静止状态,而不是移动可言,因为有一个时间,在该空间中的吊杆移动。

人类数百年努力解决的飞矢悖论的优秀思想,但是从逻辑上来看,它是由绝对真实。对于它的反驳是需要解释的有限时间间隔如何组成的无数次 - 来证明它是不可能的,甚至亚里士多德,强烈批评芝诺。亚里士多德正确地指出,时间长度不能被视为不可分割的一些孤立的瞬间的总和,但许多科学家认为,他的做法是不同的深度,并不否认一个悖论的存在。应当指出的是,问题飞行箭头的制剂芝诺追捧不否认运动的可能性,因此,而是以显示出理想的数学概念的矛盾。
8.悖论Galileya
在他的作品“关于科学两个新的分支对话和数学示威”伽利略提出了一个悖论呈现出无限集合有趣的性质。科学家制定了两个相互矛盾的判决。首先,有代表整数的其他方块数字,例如1,9,16,25,36等。有不具有该属性的其他号码 - 2,3,5,6,7,8,10,和类似物。因此,正方形和通常号码的确切总数为比仅正方形的数目更准确。第二命题:对于每一个正整数,存在一个确切的正方形,每平方有一个平方根,即,平方等于正整数的数的数量
。
基于这一矛盾,伽利略的结论是,大约仅适用于有限集合元素的数量的参数,虽然后来数学家引入的概念,该组的功率 - 与它已被证明忠诚伽利略和用于无限集合的第二判断
。
9.悖论袋kartofelya
比方说,某农民有土豆体重整整100公斤麻袋。检查其内容后,农民发现该袋保持在燥湿 - 99%的重量是水,和包含在土豆1%的其它物质。它解决了有点干土豆,它的水分含量降低至98%,运输袋在干燥的地方。第二天,事实证明,一个升(1千克)水居然蒸发,但袋子的重量从100下降到50公斤,怎么能这样?让我们计算 - 99%100公斤99公斤,干渣和水的质量最初等于1/99的那么的重量比。干燥后,水包括98%的所述袋的总重量的,所以残留物中以水的重量的干质量的比率为现在1/49。由于质量平衡没有改变,剩余的水的重量为49个公斤。
当然,细心的读者会立即检测在计算一个总的数学错误 - 一个虚构的漫画“土豆悖论炒鱿鱼”可以考虑如何使用看似“逻辑”推理“以科学为后盾”可以从字面上从头开始建立一个理论违背了共同的一个很好的例子意思。
10.悖论voronov
这个问题也被称为汉帛的悖论 - 第二个名字,她是为了纪念德国数学家卡尔·古斯塔夫·亨佩尔,它的经典版本的作者的好评。问题是配方很简单:每一个乌鸦是黑色的。由此可见,任何不黑,不会是乌鸦。该法是一个合乎逻辑的对位,也就是说,如果某个包裹“A”是“B”,否定了“B”的等于否定了“A”的结果。如果一个人看到一个黑色的乌鸦,它强化了他的信念,所有的乌鸦都是黑的颜色,这是有道理的,但是按照对位和感应的原理逻辑认为,观察对象不黑的(比如说,红苹果)也证明,所有的乌鸦都是黑色。换句话说 - 这个人住在圣彼得堡,他证明了他并不住在莫斯科
。
从逻辑悖论的角度来看,它看起来完美,但它违背了真实的生活 - 红苹果能够在没有办法证明的事实,所有的乌鸦都是黑
。
通过factroom.ru

从远古时代的学者和思想家喜欢娱乐自己和同事分期无法解决的问题,并制定各种矛盾的。其中的一些思想实验仍然适用千百年来,这表明许多流行的科学模型中普遍接受的理论的不完善和“洞”,一直被认为是根本。我们邀请您反映最有趣,最令人惊讶的自相矛盾的,因为它是现在表示,“炸毁了大脑”来代逻辑学家,哲学家和数学家。
1.绢“阿基里斯与龟”阿基里斯悖论和龟 - 悖论(逻辑真,但矛盾的说法),通过埃利亚在V-世纪公元前古希腊哲学家芝诺制定之一。其实质是:传奇英雄阿喀琉斯决定与乌龟比赛竞争。如你所知,乌龟没有什么不同prytkost,所以阿喀琉斯送给了对手一个良好的开端,在500米,当乌龟克服了这个距离,主人公以10倍的速度衬托,也就是说,直到乌龟爬50米跟腱有时间运行数据也500米赔率。然后,亚军克服未来的50米,但乌龟在这个时候爬由另外5男,似乎阿基里斯它会赶上,但对手还是要来,直到它运行5米,她设法将另一半米,等等。它们之间的距离被无限缩小,但在理论上,英雄没能赶上低迷的乌龟,它不是太大,但总是在他的前面。

当然,从物理矛盾的一点是没有意义的 - 如果跟腱快得多移动在任何情况下,他将打破前锋,但芝诺,首先,想展示他的论点是理想化的数学概念“点空间”和“时间点”是不非常适合于实际运动的正确应用。绢揭示了数学上合理之间的差异的想法,非零间隔的时间和空间可以无限分割(所以龟必须始终保持领先地位),与现实中的主人公,当然,赢得了比赛。
2.上的说法petli

悖论描述时间旅行,时间长灵感科幻小说作家和科幻电影和电视剧的创作者的来源。有时间循环的悖论几个变种,对这些问题的最简单而明显的例子之一造成的在他的著作«新的时间旅行者»(«新的时间旅行者“)大卫·图梅,马萨诸塞大学的教授。
想象一下,一个时间旅行者在书店买了莎士比亚的副本,“哈姆雷特”。然后,他去了英国,女王伊丽莎白一世的时候,维尔京,寻找威廉·莎士比亚,送了他一本书。他改写了它,并出版了他自己的。经过了几百年,“哈姆雷特”被翻译成数十种语言,无休止地重现,而另一份是在同一个书店,其中一个时间旅行者购买它,并给莎士比亚,他占用了,等等...谁在这种情况下,应考虑不朽的悲剧作家?
3.女生的矛盾和malchika

在概率论,矛盾也被称为“儿童史密斯先生”或“女士斯密问题”。它最早是由美国数学家马丁·加德纳在该杂志«科学美国人»其中一个房间内制定。科学家们争论的悖论了几十年,并有决议的几种方法。经过思考这个问题,你可以提供你自己的版本。
这个家庭有两个孩子,已知其中之一 - 一个男孩。什么是第二个孩子也有男性的概率是多少?乍一看,答案是显而易见的 - 50的50,还是他真的是男孩还是女孩,胜算必须相等。问题是,对家庭有两个孩子有男女儿童的四种可能的组合 - 两个女孩,两个男孩,大男孩和最小的女孩,反之亦然 - 一个女孩和一个男孩年长年轻。第一个可以被消除,因为孩子们完全男孩之一,但在这种情况下有三个选项,而不是两个,且第二子也是男孩的概率 - 三分之一的机会
4.矛盾茹尔丹与kartochkoyProblemu在二十个世纪初提出的英国数学家和逻辑学家菲利普·茹尔丹,可以被认为是骗子的著名悖论的变化。

想象一下 - 你持有一张卡,上面写着:“批准该卡的背面是真实的。”打开卡,你会发现这句话“的说法是错误的另一面。”你可以想像,有一个矛盾,如果第一条语句真,第二个也是如此,但在这种情况下,第一个肯定是假的。如果第一方证是假的,那么第二句不能算是真正的,这意味着第一个语句重新成为真理......更有意思的说谎者悖论的版本 - 在未来的一段
5.诡辩“鳄鱼”在河岸边是一个母亲带着孩子,突然一只鳄鱼游到他和拉孩子在水中。伤心欲绝的母亲要求她还给孩子,什么鳄鱼说,他同意给它一劫,如果一个女人正确回答他的问题:“如果他的孩子的回报”。很显然,女性两个答案 - 是或否。如果她认为,鳄鱼会给她一个孩子,这一切都取决于动物 - 考虑到答案真正的小偷放过孩子,如果他说,他的母亲是错误的,她没看到孩子,根据条约的规定
。

对一个女人产生负响应相当复杂的一切 - 如果这是真的,小偷必须履行的交易的条款和释放孩子,但他的母亲,这样的回答并不符合现实。为了确保这种反应是虚假的,鳄鱼就要还给孩子的母亲,但这违背了协议,因为它的误差必须留下鳄鱼的孩子。
值得一提的是,提出鳄鱼的交易,蕴含着逻辑上的矛盾,所以他的承诺是不可能的。这个经典的诡辩的作者认为雪城,谁住在V世纪公元前扬声器,思想家,政治家CORAX。
6.绢“二分法”

埃利亚的芝诺的悖论另外,表现出运动的不正确理想化的数学模型。这个问题可以把这种方式 - 让我们说你准备从开始到结束都要经过你的城市的一些街道。要做到这一点,你需要克服其前半,然后一半,剩下的一半,那么一半的下一个段的,依此类推。换句话说 - 你经过距离的一半,那么四分之一,八分之一,十六分之一 - 降低的路径段的数量趋于无穷,因为任何剩余部分可以分为两部分,然后一路完全不可能。换句话说乍一看矛盾有所牵强,芝诺想证明数学规律是违背现实的,因为事实上,你可以很容易地通过所有走的无影无踪。
7.绢“飞矢”埃利亚的芝诺的悖论著名触动最深的矛盾有关的时间和运动性科学家的意见。绢公式表示为:从弓的箭射击,它仍然是固定的,因为在任何时候它是静止的,未做举动。如果在任何时候箭头静止状态,那么它总是在静止状态,而不是移动可言,因为有一个时间,在该空间中的吊杆移动。

人类数百年努力解决的飞矢悖论的优秀思想,但是从逻辑上来看,它是由绝对真实。对于它的反驳是需要解释的有限时间间隔如何组成的无数次 - 来证明它是不可能的,甚至亚里士多德,强烈批评芝诺。亚里士多德正确地指出,时间长度不能被视为不可分割的一些孤立的瞬间的总和,但许多科学家认为,他的做法是不同的深度,并不否认一个悖论的存在。应当指出的是,问题飞行箭头的制剂芝诺追捧不否认运动的可能性,因此,而是以显示出理想的数学概念的矛盾。
8.悖论Galileya

在他的作品“关于科学两个新的分支对话和数学示威”伽利略提出了一个悖论呈现出无限集合有趣的性质。科学家制定了两个相互矛盾的判决。首先,有代表整数的其他方块数字,例如1,9,16,25,36等。有不具有该属性的其他号码 - 2,3,5,6,7,8,10,和类似物。因此,正方形和通常号码的确切总数为比仅正方形的数目更准确。第二命题:对于每一个正整数,存在一个确切的正方形,每平方有一个平方根,即,平方等于正整数的数的数量
。
基于这一矛盾,伽利略的结论是,大约仅适用于有限集合元素的数量的参数,虽然后来数学家引入的概念,该组的功率 - 与它已被证明忠诚伽利略和用于无限集合的第二判断
。
9.悖论袋kartofelya

比方说,某农民有土豆体重整整100公斤麻袋。检查其内容后,农民发现该袋保持在燥湿 - 99%的重量是水,和包含在土豆1%的其它物质。它解决了有点干土豆,它的水分含量降低至98%,运输袋在干燥的地方。第二天,事实证明,一个升(1千克)水居然蒸发,但袋子的重量从100下降到50公斤,怎么能这样?让我们计算 - 99%100公斤99公斤,干渣和水的质量最初等于1/99的那么的重量比。干燥后,水包括98%的所述袋的总重量的,所以残留物中以水的重量的干质量的比率为现在1/49。由于质量平衡没有改变,剩余的水的重量为49个公斤。
当然,细心的读者会立即检测在计算一个总的数学错误 - 一个虚构的漫画“土豆悖论炒鱿鱼”可以考虑如何使用看似“逻辑”推理“以科学为后盾”可以从字面上从头开始建立一个理论违背了共同的一个很好的例子意思。
10.悖论voronov

这个问题也被称为汉帛的悖论 - 第二个名字,她是为了纪念德国数学家卡尔·古斯塔夫·亨佩尔,它的经典版本的作者的好评。问题是配方很简单:每一个乌鸦是黑色的。由此可见,任何不黑,不会是乌鸦。该法是一个合乎逻辑的对位,也就是说,如果某个包裹“A”是“B”,否定了“B”的等于否定了“A”的结果。如果一个人看到一个黑色的乌鸦,它强化了他的信念,所有的乌鸦都是黑的颜色,这是有道理的,但是按照对位和感应的原理逻辑认为,观察对象不黑的(比如说,红苹果)也证明,所有的乌鸦都是黑色。换句话说 - 这个人住在圣彼得堡,他证明了他并不住在莫斯科
。
从逻辑悖论的角度来看,它看起来完美,但它违背了真实的生活 - 红苹果能够在没有办法证明的事实,所有的乌鸦都是黑
。
通过factroom.ru