875
10 entertaining logical paradoxes
If after reading this collection, you do not mess up completely, so you think enough yasno
Scholars and thinkers from ancient times love to entertain themselves and colleagues staging unsolvable problems and formulating various kinds of paradoxes. Some of these thought experiments remain relevant for thousands of years, indicating that the imperfection of many popular scientific models and "holes" in the generally accepted theories, has long been considered fundamental. We invite you to reflect on the most interesting and surprising paradox that, as it is now expressed, "blew up the brain" to generations of logicians, philosophers and mathematicians.
1. Aporia "Achilles and the tortoise" paradox of Achilles and the tortoise - one of the paradoxes (logically true but contradictory statements), formulated by the ancient Greek philosopher Zeno of Elea in the V-th century BC. Its essence is as follows: the legendary hero Achilles decided to compete in the race with a turtle. As you know, turtles do not differ prytkost, so Achilles gave his opponent a head start in the 500 meters. When the turtle overcomes this distance, the hero sets off at a rate of 10 times greater, that is, until the turtle crawls 50 meters, Achilles has time to run the data it 500m odds . Then the runner overcomes the next 50 meters, but the tortoise at this time crawls by another 5 m, it seems that Achilles was about it will catch up, but the opponent is still to come, and until it runs 5 meters, she manages to move for another half a meter, and so on. The distance between them is infinitely reduced, but in theory, the hero did not manage to catch up with the sluggish turtle, it is not much, but always ahead of him.
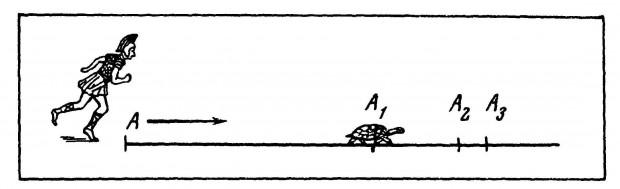
Of course, from the point of view of physics paradox it makes no sense - if Achilles is moving much faster in any case he will break forward, but Zeno, first of all, wanted to show his arguments that the idealized mathematical concepts "point in space" and "point in time" is not very appropriate for the correct application of the real movement. Aporia reveals a discrepancy between the mathematically justified by the idea that non-zero intervals of space and time can be divided infinitely (so the turtle must always stay ahead) and the reality in which the hero, of course, wins the race.
2. The paradox of time petli
Paradoxes describing travel in time, for a long time a source of inspiration for science fiction writers and creators of science fiction films and TV series. There are several variants of the paradoxes of the time loop, one of the most simple and obvious examples of such problems resulted in his book «The New Time Travelers» («New Time Traveler") David Toomey, a professor at the University of Massachusetts.
Imagine what a time traveler had bought in a bookstore a copy of Shakespeare's "Hamlet." He then went to England, the time of Queen Elizabeth I, the Virgin and look for William Shakespeare, presented him with a book. He rewrote it and published as his own. Pass for hundreds of years, "Hamlet" is translated into dozens of languages, endlessly reproduced, and one copy is in the same bookstore, where a time traveler buys it and gives Shakespeare, and he takes up, and so on ... Who in this case should be considered author of the immortal tragedy?
3. The paradox of girls and malchika
In probability theory, the paradox is also called the "Children of Mr. Smith" or "Mrs. Smith Problem". It was first formulated by the American mathematician Martin Gardner in one of the rooms of the magazine «Scientific American». Scientists argue over paradox for decades, and there are several ways of its resolution. After thinking about the problem, and you can offer your own version.
The family has two children, and it is known that one of them - a boy. What is the probability that the second child also has male sex? At first glance, the answer is obvious - 50 of 50, or he really a boy or a girl, the odds have to be equal. The problem is that for families with two children there are four possible combinations of the sexes children - two girls, two boys, the eldest boy and the youngest girl and vice versa - a girl and a boy older younger. The first can be eliminated, as one of the children exactly the boy, but in this case are three options rather than two, and the probability that the second child is also a boy - one chance in three.
4. The paradox Jourdain with kartochkoyProblemu proposed by British mathematician and logician Philippe Jourdain at the beginning of XX-th century, can be considered a variation of the famous paradox of the liar.

Imagine - you are holding a card that says: "Approval of the back of the card is true." Turning the card, you will find the phrase "The statement is false on the other side." As you can imagine, there is a contradiction if the first statement true, the second is also true, but in this case, the first must be false. If the first party card is false, then the second sentence can not be regarded as true, which means the first statement again becomes the truth ... Even more interesting version of the paradox of the liar - in the next paragraph.
5. sophistry "Crocodile" on the banks of the river are a mother with a child, suddenly a crocodile swims to him and pulls the child in the water. Inconsolable mother asks her to return the child, what the crocodile says he agreed to give it unharmed, if a woman the right answer to his question: "The return of the child if he did?". It is clear that women are two answers - yes or no. If she argues that the crocodile would give her a child, it all depends on the animal - considering the answer true thief let go of the child, if he says that his mother was wrong, that she did not see the child, according to the rules of the treaty.

A negative response to a woman considerably complicates everything - if it is true, the thief must fulfill the terms of the transaction and release the child, but the mother so that the answer does not correspond to reality. To ensure that the falsity of such a response, the crocodile is necessary to return the child the mother, but this contradicts the agreement because its error must leave the child of a crocodile.
It is worth noting that the deal proposed by the crocodile, contains a logical contradiction, so his promise impossible. The author of this classical sophism regarded speaker, thinker and politician Corax of Syracuse, who lived in the V-th century BC.
6. Aporia "Dichotomy"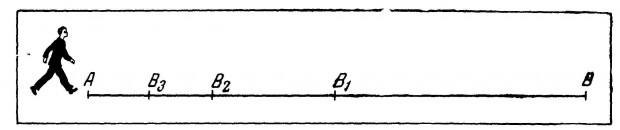
Another paradox of Zeno of Elea, showing incorrect idealized mathematical model of movement. The problem can be put this way - let's say you set out to go through some streets of your city from the beginning to the end. To do this you need to overcome its first half, then half of the remaining half, then half of the next segment, and so on. In other words - you go through half of the distance, then a quarter, one-eighth, one sixteenth - decreasing the number of segments of the path tends to infinity, as any remaining part can be divided into two parts, then go all the way entirely impossible. Stated somewhat far-fetched at first glance a paradox, Zeno wanted to show that mathematical laws are contrary to reality, because in fact you can easily pass all away without a trace.
7. Aporia "Flying Arrow" The famous paradox of Zeno of Elea touches the deepest contradictions in the views of scientists about the nature of time and movement. Aporia formulated as: an arrow shot from a bow, it remains stationary, as at any time it is at rest, without making move. If at any time the arrow rest, then it is always in a state of rest and not moving at all, since there is a time at which the boom moves in space.

Outstanding minds of mankind for centuries trying to solve the paradox of the flying arrow, but from a logical point of view, it is made absolutely true. For its refutation is required to explain how the finite time interval can consist of an infinite number of times - to prove it was not possible even to Aristotle, strongly criticized Zeno. Aristotle rightly pointed out that length of time can not be considered as a sum of some indivisible isolated moments, but many scientists believe that his approach is different depth and does not deny the existence of a paradox. It should be noted that the formulation of the problem flying arrow Zeno sought not deny the possibility of movement, as such, but to reveal the contradictions in the idealistic mathematical concepts.
8. The paradox Galileya
In his work "Conversations and mathematical demonstrations concerning two new branches of science" Galileo Galilei proposed a paradox showing interesting properties of infinite sets. The scientist formulated two conflicting judgments. First, there are numbers representing the other squares of integers, such as 1, 9, 16, 25, 36 and so on. There are other numbers that do not have this property - 2, 3, 5, 6, 7, 8, 10, and the like. Thus, the exact total number of squares and the usual numbers to be more accurate than the number of squares only. The second proposition: for every positive integer there exists an exact square, and each square there is a square root, that is, the number of squares equal to the number of positive integers.
Based on this contradiction, Galileo concluded that the arguments about the number of elements applied only to finite sets, although later mathematicians introduced the concept, the power of the set - with it has been proven loyalty to the second judgment of Galileo and for infinite sets.
9. The paradox bag kartofelya
Let's say a certain farmer has a sack of potatoes weighing exactly 100 kg. After examining its contents, a farmer discovers that the bag was kept in dampness - 99% of its weight is water, and 1% other substances contained in potatoes. It solves bit dried potatoes, the water content in it decreased to 98% and transports the bag in a dry place. The next day, it turns out that one liter (1 kg) of water actually evaporated, but the weight of the bag fell from 100 to 50 kg, how can this be? Let's count - 99% of 100 kg is 99 kg, then the weight ratio of dry residue and water mass initially equal to 1/99. After drying, the water comprises 98% of the total weight of the bag, so the ratio of dry mass of the residue to the weight of water is now 1/49. Since the mass balance has not changed, remaining water weighs 49 kg.
Of course, the attentive reader will immediately detect a gross mathematical error in the calculation - an imaginary comic "paradox sack of potatoes" can be considered an excellent example of how to use the seemingly "logical" and "scientifically backed by" reasoning can literally from scratch to build a theory contrary to the common meaning.
10. The paradox voronov
The problem is also known as the paradox of Hempel - the second name she received in honor of the German mathematician Carl Gustav Hempel, the author of its classical version. The problem is formulated quite simple: every raven is black. It follows that anything that is not black, not be a raven. This law is a logical contraposition, that is, if a certain parcel "A" is the result of "B", the denial of the "B" tantamount to denying the "A". If a person sees a black crow, it reinforces his belief that all crows are black color, which makes sense, but in accordance with the contraposition and the principle of induction logically argue that the observation of objects not black (say, red apples) also proves that all crows are colored black. In other words - that the person lives in St. Petersburg he proves that he does not live in Moscow.
From the standpoint of logic paradox it looks perfectly, but it is contrary to real life - red apples can in no way confirms the fact that all crows are black.
via factroom.ru

Scholars and thinkers from ancient times love to entertain themselves and colleagues staging unsolvable problems and formulating various kinds of paradoxes. Some of these thought experiments remain relevant for thousands of years, indicating that the imperfection of many popular scientific models and "holes" in the generally accepted theories, has long been considered fundamental. We invite you to reflect on the most interesting and surprising paradox that, as it is now expressed, "blew up the brain" to generations of logicians, philosophers and mathematicians.
1. Aporia "Achilles and the tortoise" paradox of Achilles and the tortoise - one of the paradoxes (logically true but contradictory statements), formulated by the ancient Greek philosopher Zeno of Elea in the V-th century BC. Its essence is as follows: the legendary hero Achilles decided to compete in the race with a turtle. As you know, turtles do not differ prytkost, so Achilles gave his opponent a head start in the 500 meters. When the turtle overcomes this distance, the hero sets off at a rate of 10 times greater, that is, until the turtle crawls 50 meters, Achilles has time to run the data it 500m odds . Then the runner overcomes the next 50 meters, but the tortoise at this time crawls by another 5 m, it seems that Achilles was about it will catch up, but the opponent is still to come, and until it runs 5 meters, she manages to move for another half a meter, and so on. The distance between them is infinitely reduced, but in theory, the hero did not manage to catch up with the sluggish turtle, it is not much, but always ahead of him.

Of course, from the point of view of physics paradox it makes no sense - if Achilles is moving much faster in any case he will break forward, but Zeno, first of all, wanted to show his arguments that the idealized mathematical concepts "point in space" and "point in time" is not very appropriate for the correct application of the real movement. Aporia reveals a discrepancy between the mathematically justified by the idea that non-zero intervals of space and time can be divided infinitely (so the turtle must always stay ahead) and the reality in which the hero, of course, wins the race.
2. The paradox of time petli

Paradoxes describing travel in time, for a long time a source of inspiration for science fiction writers and creators of science fiction films and TV series. There are several variants of the paradoxes of the time loop, one of the most simple and obvious examples of such problems resulted in his book «The New Time Travelers» («New Time Traveler") David Toomey, a professor at the University of Massachusetts.
Imagine what a time traveler had bought in a bookstore a copy of Shakespeare's "Hamlet." He then went to England, the time of Queen Elizabeth I, the Virgin and look for William Shakespeare, presented him with a book. He rewrote it and published as his own. Pass for hundreds of years, "Hamlet" is translated into dozens of languages, endlessly reproduced, and one copy is in the same bookstore, where a time traveler buys it and gives Shakespeare, and he takes up, and so on ... Who in this case should be considered author of the immortal tragedy?
3. The paradox of girls and malchika

In probability theory, the paradox is also called the "Children of Mr. Smith" or "Mrs. Smith Problem". It was first formulated by the American mathematician Martin Gardner in one of the rooms of the magazine «Scientific American». Scientists argue over paradox for decades, and there are several ways of its resolution. After thinking about the problem, and you can offer your own version.
The family has two children, and it is known that one of them - a boy. What is the probability that the second child also has male sex? At first glance, the answer is obvious - 50 of 50, or he really a boy or a girl, the odds have to be equal. The problem is that for families with two children there are four possible combinations of the sexes children - two girls, two boys, the eldest boy and the youngest girl and vice versa - a girl and a boy older younger. The first can be eliminated, as one of the children exactly the boy, but in this case are three options rather than two, and the probability that the second child is also a boy - one chance in three.
4. The paradox Jourdain with kartochkoyProblemu proposed by British mathematician and logician Philippe Jourdain at the beginning of XX-th century, can be considered a variation of the famous paradox of the liar.

Imagine - you are holding a card that says: "Approval of the back of the card is true." Turning the card, you will find the phrase "The statement is false on the other side." As you can imagine, there is a contradiction if the first statement true, the second is also true, but in this case, the first must be false. If the first party card is false, then the second sentence can not be regarded as true, which means the first statement again becomes the truth ... Even more interesting version of the paradox of the liar - in the next paragraph.
5. sophistry "Crocodile" on the banks of the river are a mother with a child, suddenly a crocodile swims to him and pulls the child in the water. Inconsolable mother asks her to return the child, what the crocodile says he agreed to give it unharmed, if a woman the right answer to his question: "The return of the child if he did?". It is clear that women are two answers - yes or no. If she argues that the crocodile would give her a child, it all depends on the animal - considering the answer true thief let go of the child, if he says that his mother was wrong, that she did not see the child, according to the rules of the treaty.

A negative response to a woman considerably complicates everything - if it is true, the thief must fulfill the terms of the transaction and release the child, but the mother so that the answer does not correspond to reality. To ensure that the falsity of such a response, the crocodile is necessary to return the child the mother, but this contradicts the agreement because its error must leave the child of a crocodile.
It is worth noting that the deal proposed by the crocodile, contains a logical contradiction, so his promise impossible. The author of this classical sophism regarded speaker, thinker and politician Corax of Syracuse, who lived in the V-th century BC.
6. Aporia "Dichotomy"

Another paradox of Zeno of Elea, showing incorrect idealized mathematical model of movement. The problem can be put this way - let's say you set out to go through some streets of your city from the beginning to the end. To do this you need to overcome its first half, then half of the remaining half, then half of the next segment, and so on. In other words - you go through half of the distance, then a quarter, one-eighth, one sixteenth - decreasing the number of segments of the path tends to infinity, as any remaining part can be divided into two parts, then go all the way entirely impossible. Stated somewhat far-fetched at first glance a paradox, Zeno wanted to show that mathematical laws are contrary to reality, because in fact you can easily pass all away without a trace.
7. Aporia "Flying Arrow" The famous paradox of Zeno of Elea touches the deepest contradictions in the views of scientists about the nature of time and movement. Aporia formulated as: an arrow shot from a bow, it remains stationary, as at any time it is at rest, without making move. If at any time the arrow rest, then it is always in a state of rest and not moving at all, since there is a time at which the boom moves in space.

Outstanding minds of mankind for centuries trying to solve the paradox of the flying arrow, but from a logical point of view, it is made absolutely true. For its refutation is required to explain how the finite time interval can consist of an infinite number of times - to prove it was not possible even to Aristotle, strongly criticized Zeno. Aristotle rightly pointed out that length of time can not be considered as a sum of some indivisible isolated moments, but many scientists believe that his approach is different depth and does not deny the existence of a paradox. It should be noted that the formulation of the problem flying arrow Zeno sought not deny the possibility of movement, as such, but to reveal the contradictions in the idealistic mathematical concepts.
8. The paradox Galileya

In his work "Conversations and mathematical demonstrations concerning two new branches of science" Galileo Galilei proposed a paradox showing interesting properties of infinite sets. The scientist formulated two conflicting judgments. First, there are numbers representing the other squares of integers, such as 1, 9, 16, 25, 36 and so on. There are other numbers that do not have this property - 2, 3, 5, 6, 7, 8, 10, and the like. Thus, the exact total number of squares and the usual numbers to be more accurate than the number of squares only. The second proposition: for every positive integer there exists an exact square, and each square there is a square root, that is, the number of squares equal to the number of positive integers.
Based on this contradiction, Galileo concluded that the arguments about the number of elements applied only to finite sets, although later mathematicians introduced the concept, the power of the set - with it has been proven loyalty to the second judgment of Galileo and for infinite sets.
9. The paradox bag kartofelya

Let's say a certain farmer has a sack of potatoes weighing exactly 100 kg. After examining its contents, a farmer discovers that the bag was kept in dampness - 99% of its weight is water, and 1% other substances contained in potatoes. It solves bit dried potatoes, the water content in it decreased to 98% and transports the bag in a dry place. The next day, it turns out that one liter (1 kg) of water actually evaporated, but the weight of the bag fell from 100 to 50 kg, how can this be? Let's count - 99% of 100 kg is 99 kg, then the weight ratio of dry residue and water mass initially equal to 1/99. After drying, the water comprises 98% of the total weight of the bag, so the ratio of dry mass of the residue to the weight of water is now 1/49. Since the mass balance has not changed, remaining water weighs 49 kg.
Of course, the attentive reader will immediately detect a gross mathematical error in the calculation - an imaginary comic "paradox sack of potatoes" can be considered an excellent example of how to use the seemingly "logical" and "scientifically backed by" reasoning can literally from scratch to build a theory contrary to the common meaning.
10. The paradox voronov

The problem is also known as the paradox of Hempel - the second name she received in honor of the German mathematician Carl Gustav Hempel, the author of its classical version. The problem is formulated quite simple: every raven is black. It follows that anything that is not black, not be a raven. This law is a logical contraposition, that is, if a certain parcel "A" is the result of "B", the denial of the "B" tantamount to denying the "A". If a person sees a black crow, it reinforces his belief that all crows are black color, which makes sense, but in accordance with the contraposition and the principle of induction logically argue that the observation of objects not black (say, red apples) also proves that all crows are colored black. In other words - that the person lives in St. Petersburg he proves that he does not live in Moscow.
From the standpoint of logic paradox it looks perfectly, but it is contrary to real life - red apples can in no way confirms the fact that all crows are black.
via factroom.ru