Розваги на площині Лобачевського

Літак Euclidean є нудним. Доступний простір тільки виростає як квадрат радіусу зору. У порівнянні з площиною Лобачевського є гігантик. Тексти пісень, а це означає: Але є життя занадто!
Сума кутів полігону тут менше, ніж у Euclid і не є постійними, але залежить від площі (відвідте тут цікавий наслідок полягає в тому, що є найбільші трикутники, чотири-п'ятикутні і тп кути, сума кутів, які стає рівною). Тому є перекриття площини з будь-яким правильним полігонами, якщо вони досить великі. У статті про гру життя використовується тротуар з чотирикутниками, п'ять чотирикутних трикутників конверж. Але ці чотирикутники дуже великі. Якщо ви відмовляєтеся від однаковості полігонів, можна взяти тротуар з регулярних шестикутників і пектагонів. Для нього можна зробити візуальну модель літака з магнітних кульок "Неокубе".


Полігони будуть кільцями шести і сім кульок. Каблучки можна об'єднати разом. Якщо вони однакові орієнтації (напрямок магнітного поля в кільце), вони долучаються до ребра двох кульок, якщо різні - ребрами з верхнім. Кожен гептегон знаходиться в контакті з семи шестикутниками.


Кожен шестигранник має три шестигранники і три шестигранники.
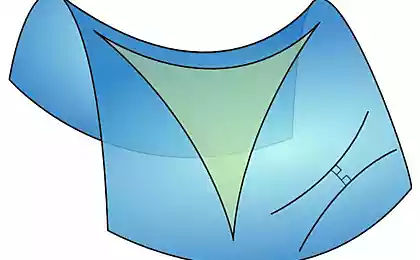
Невеликий фрагмент літака починає збиратися в складках, з подальшим зростанням не можна класти в наш простір. Але можна нарізати смугу рівної ширини (обмежено не прямими, але при гіперциклах), потім її можна скласти в спіраль.
Комп'ютер не так багато обмежується геометрією реального простору і ви можете прогулятися по площині Лобачевського в гіперлогі. Граючи цю гру ви можете відчути деякі особливості гіперболічної геометрії. П'ятогорського теореми написано наступним чином: пн-пт: пт (a) п(б) (Ч вказує гіперболічний козин). На невеликій довжині перетворюється в звичайну теорему Пітагоран (це легко перевірено декомпозицією ch в серії Taylor до другого ступеня). На великій (ч стає майже рівним до половини експонентів), гіпотенуза підходить до простої суми катета. Що таке, що ведеться проти краю, не робить багато сенсу і бігає подалі стає простіше, ніж зловживати. Довжина кола схильна до вибуху радіусу - обходу перешкод виходить дуже довго.
На жаль, я не знайшов стратегічних ігор на площині Лобачевського. Так як по периметру і площі фігур виростають про те ж, контроль великої площі не дасть серйозної переваги при захисті кордонів. І з тих пір, коли площа кола зростає, можливо, буде компактно розмістити величезні підіймки. Я думаю, що б зробити гру більш цікавим.
Ми можемо самі зателефонувати одержувачу.

Джерело: geektimes.ru/post/243829/