Entertainment on the Lobachevsky plane

Euclidean plane is boring. Available space increases only as the square of the radius of the review. Compared with her gigantic expanse of the Lobachevsky plane. But there are life !
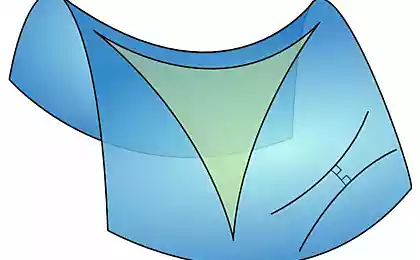
Sum of the angles of a polygon is less than that of Euclid and not constant, but depends on the area (from here interesting consequence - there are very large triangles, pentagons and four m squares, the sum of the angles of which becomes equal to zero). According to this there are tilings of the plane any regular polygons if they are large enough. The article about the game of life is used tiling quadrangles, in each vertex five quadrangles. But these quads are very large. If we abandon the similarity of polygons, you can take a tiling of regular hexagons and heptagons. For it is possible to make a visual model of the plane of the magnetic beads "Neokub».


Polygons are rings of six and seven balls. Rings can be interconnected. If they are the same direction (direction of the magnetic field in the ring), they engage with the edges of the two balls if different - a rib apex. Each heptagon contact with family hexagons.


Each hexagon - heptagon with three and three hexagons.
A small piece of the plane starts to gather in the folds, with a further increase in our space to lay it no longer works. But you can cut a strip of equal width (limited not directly, but гиперциклами), then it can be rolled into a spiral.
The computer is not so much limited by the geometry of the real space and walk on the Lobachevsky plane can be hyperrogue . After playing this game you can feel some of the features of hyperbolic geometry. The local version of the Pythagorean theorem is written as: ch © = ch (a) ch (b) (denoted by ch гиперболический cosine ). For small values ​​of the lengths he had to change into an ordinary Pythagorean theorem (This is easily seen by expanding the ch in a Taylor series up to the second degree). For large (ch becomes almost equal to half the exponent) - hypotenuse is close to a simple sum of the other two sides. That is to run across the path of a large does not make sense to run away and become easier than catching up. Circumference tends to exponentially radius - avoid obstacles get a very long time.
Unfortunately, strategy games on the Lobachevsky plane I have not found. Since the perimeter and area of ​​shapes is growing at about the same, control a large area will not give significant benefits in the defense of the borders. And as the area of ​​a circle is growing exponentially, could be compactly placed huge army. In my opinion, it would make the game more interesting.
It is a pity that the geometry of our world in the foreseeable scale is not hyperbolic ...

Source: geektimes.ru/post/243829/