Entretenimiento en el plano Lobachevsky

plano euclidiana es aburrido. Espacio disponible sólo aumenta con el cuadrado del radio de la revisión. En comparación con su extensión gigantesca del plano Lobachevsky. Pero hay !
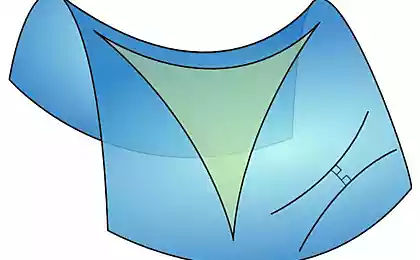
Suma de los ángulos de un polígono es menor que la de Euclides y no es constante, sino que depende de la zona (desde consecuencia aquí interesante - no son muy grandes triángulos, pentágonos y cuatro cuadrados m, la suma de los ángulos de los cuales se hace igual a cero). De acuerdo con esto, hay teselaciones del plano cualquier polígonos regulares si ellos son lo suficientemente grandes. El artículo sobre el juego de la vida se utiliza cuadriláteros embaldosado, en cada vértice cinco cuadriláteros. Pero estos quads son muy grandes. Si abandonamos la semejanza de polígonos, puede tomar un mosaico de hexágonos regulares y heptágonos. Para ello es posible hacer un modelo visual del plano de las perlas magnéticas "Neokub».


Los polígonos son anillos de seis y siete bolas. Los anillos pueden estar interconectadas. Si son la misma dirección (dirección del campo magnético en el anillo), que se acoplan con los bordes de las dos bolas si es otra - un ápice costilla. Cada contacto heptágono con hexágonos de la familia.


Cada hexágono - heptágono con tres y tres hexágonos
. Un pequeño trozo del avión comienza a reunirse en los pliegues, con un incremento adicional en nuestro espacio para sentar ya no funciona. Pero usted puede cortar una tira de igual anchura (limitado no directamente, pero гиперциклами), a continuación, se puede enrollar en una espiral.
El equipo no está limitado tanto por la geometría del espacio real y caminar en el plano Lobachevsky puede ser hyperrogue . Después de jugar este juego puedes sentir algunas de las características de la geometría hiperbólica. La versión local del teorema de Pitágoras se escribe como: ch © = ch (a) ch (b) (denotado por ch гиперболический coseno). Para valores pequeños de la longitud que tenía que cambiar en un teorema de Pitágoras ordinaria (Esto se ve fácilmente mediante la ampliación de la ch en una serie de Taylor hasta el segundo grado). Para grandes (ch vuelve casi igual a la mitad el exponente) - hipotenusa está cerca de una simple suma de los otros dos lados. Eso es correr a través de la trayectoria de un gran no tiene sentido de huir y llegar a ser más fácil que ponerse al día. Circunferencia tiende al radio exponencialmente - evitar obstáculos consiguen mucho tiempo
. Por desgracia, los juegos de estrategia en el plano Lobachevsky no he encontrado. Desde el perímetro y el área de figuras está creciendo casi al mismo, controlar un área grande no dará beneficios significativos en la defensa de las fronteras. Y así como el área de un círculo está creciendo exponencialmente, podría ser colocado de forma compacta enorme ejército. En mi opinión, sería hacer el juego más interesante.
Es una lástima que la geometría de nuestro mundo en la escala previsible no es hiperbólico ...

Fuente: geektimes.ru/post/243829/