娱乐上的罗巴切夫斯基飞机

欧几里德飞机很无聊。可用空间增加仅作为审查的半径的平方。与她巨大的罗巴切夫斯基平面袤比较。但也有生活！
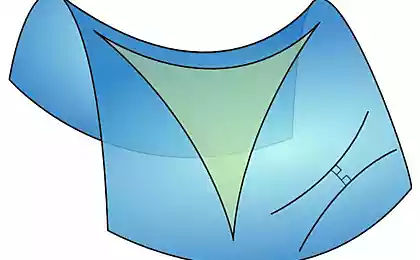
多边形的角的总和小于欧几里德，而不是恒定的，而是依赖于区域（从这里有趣的结果 - 有非常大的三角形，五边形和4米正方形，它变得等于零的角度之和）。根据该有平面的平铺如果任何正多边形它们足够大。有关游戏人生的文章使用平铺四合院，每个顶点5四合院。但这些四边形都非常大。如果我们放弃多边形的相似性，可以采取正六边形和七边形平铺。为它能够使的磁珠“Neokub»平面的可视化模型。


多边形是六，七球环。戒指可以互连。如果它们是相同的方向（磁场在环形方向上），它们啮合两个球，如果不同的边缘 - 一个肋先端。与家人六边形各七边形的接触。


每个六边形 - 七边形有三个和三个六边形
。 一小块的飞机开始聚集在褶皱，在我们的空间进一步增加奠定它不再起作用。不过你可以削减同等宽度的条（未直接限制，但<一个href="https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D0%B2%D0%B8%D0%B4%D0%B8%D1%81%D1%82%D0%B0%D0%BD%D1%82%D0%B0">гиперциклами),然后它可以被卷成螺旋形。
计算机是没有那么多的真实空间的几何形状的限制，走在罗巴切夫斯基平面可以 hyperrogue 。玩这个游戏后，你可以感受到一些双曲几何的特点。勾股定理的本地版本被写为：的 CH©= CH（一）CH（二） B>（用CH <一href="https://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%BF%D0%B5%D1%80%D0%B1%D0%BE%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8">гиперболический余弦）。因为他必须改变成普通勾股定理的长度小的值（这是很容易看到通过展开泰勒级数中的ch到第二程度）。对于大型（CH变得几乎等于一半的指数） - 斜边靠近另外两个边的简单相加。这是整个大的路径运行无厘头逃跑，并变得比追赶更容易。围趋于成倍半径 - 避开障碍物得到一个很长的时间
。 不幸的是，我还没有发现对罗巴切夫斯基飞机战略游戏。因为形状的周长和面积正以大约相同的，控制在边界的防御大面积不会给显著好处。而作为一个圆的面积是呈几何级数增长，可以紧凑放置庞大的军队。在我看来，这将让游戏变得更加有趣。
可惜的是，我们的世界在可预见的规模几何并不夸张...

来源： geektimes.ru/post/243829/