505
刮痧公设
作者irygaev
你肯定听说过,在罗巴切夫斯基几何平行线相交。当然,这不是。甚至相反。
从学校的几何当然,我们知道,[以下简称尔冬升]“通过不就行了点,可以画出一条线平行的直线这一点,也是唯一一个»。
这种说法 - 最流行的意译欧几里得的第五公设,谁曾放置了一个沉重的猪他的追随者。在其“元素”前四个公设配方很浅显的事实。在这里,他们是:
1.从任何角度任何时候,你可以画一条直线[只有一]
2.限线可以连续保持在一条直线上。
3.在所有的每一个解决方案可谓是一个圆的中心。
4.所有的直角相等。
在第五公设欧几里得决定potrollit数学家,而是写一些简单的“矩形存在”(就是这样!),他开始迷惑:“如果一条直线相交的两条直线,使内部单向角......等等等等等等...“
每个人都认为:这是黑暗的这里,能不能成为这样一个复杂的公理。不承认的伎俩,数学2000年试图摆脱这个假设,并通过其他公设和公理证明这一点。起初,希腊人,然后是阿拉伯人,然后是欧洲人。每个人都认为他成功地证明了这个前提,但后来事实证明,证明是基于一些明显的,但不能证明该说法无异于推测。这种说法已经积累了巨大的集合。下面是其中一些:
1.有三角形任意大区
2.有相似三角形
3.一个三角形的内角之和为180°
4.勾股定理是真实的
5.圆周的直径之比 - 恒定并等于π
6.两行平行的第三是相互平行
最后一点,并起着罗巴切夫斯基的几何形状的混乱了关键作用。但在更多的后来。
最后,最先进的数学家开始尝试证据应用于相反[欧几里得] - 也就是说,我们假定第五公是不正确的,并从这个任何矛盾推断。首先是意大利Saccheri(第十八世纪上半叶),这是非常恼火,他不觉得这是一个矛盾。最后,他在计算中的错误,我们得到一个矛盾,并愉快地叹了口气。
渐渐地,数学家开始怀疑的东西。而尝试了放弃第五公设是不是找一对矛盾,但只是为了看看会发生什么。第一个成功实现兰伯特,在十八世纪下半叶谁。他建立在球体,其中三角形的内角之和总是大于180°,并且所有的线相交一致的几何形状。然而,在球面几何被干扰不仅是第五公而且至少前三。顺便说一下,所述第四静止已被证实,并排除在公设。
兰伯特还研究几何,其中三角形的内角之和总是小于180度,没有发现它的冲突,但无法想象这样乱说一个假想的球体。因此,他不追求这个问题,限制了说法,这是无法证明的第五公设。
在这个施韦卡特和高斯进一步的工作。高斯完全明白了一切,但他也知道什么擦这种古老的科学团体 - 我们自己的危险。 Zaminusili,则事能够发布。因此,他们都悄无声息自己变成一个管。
第一谁公开宣布非欧几何是罗巴切夫斯基。首先,在发表的一份报告于1826年,然后在1829年。当然,这一切下雨的颠簸,他几乎失去了他的岗位作为喀山大学校长。他被人误解和嘲笑,无论是在俄罗斯和国外。但是他继续坚持和立场,并移动到最远的几何形状的一项新的研究。且自那时起他的名字命名。
几乎像在歌曲唱:
一个值得信贷,一是应有的责任
而尼古拉·伊万诺维奇·罗巴切夫斯基是他的名字
无论罗巴切夫斯基,但三年后,他发表了他对非欧几何的工作,匈牙利数学家波尔约,也依然被忽视。
高斯赞赏罗巴切夫斯基的工作,但只有在私人信件。他甚至想学习俄语读他的俄语出版。 1860年(后死亡,高斯,和罗巴切夫斯基)高斯函授成为公众和有关罗巴切夫斯基好评如潮提请注意的俄罗斯科学家和他的想法。在一般情况下,正义得到了伸张,但一如既往追授。
所以,在通过相同的点的几何罗巴切夫斯基可以由至少两条直线平行于此,但一般是无限的。这似乎是一次平行线穿过一个点,它们相交。是的,它们重叠,但诀窍是它们不彼此平行,尽管这两个平行的第三线。
再说,当你可能猜到,一个三角形的内角之和总是小于180°时,通过圆周的恒定比率一定到与圆等的直径增加的三角形的面积这样的东西。而勾股定理是行不通的。
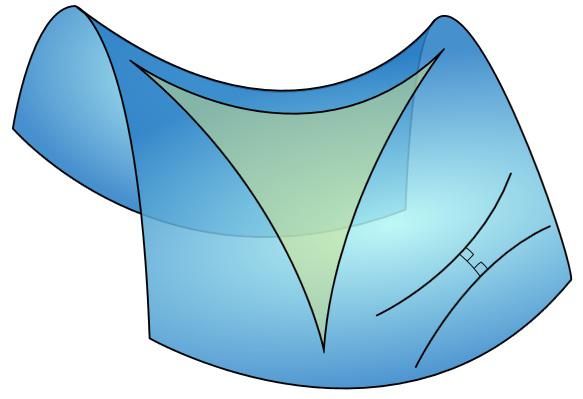
如何提出一个表面罗巴切夫斯基几何上的工作?在这里,它是 - 在KDPV,有一个非常性感的她一个三角形。这个所谓双曲平面。如果球 - 无处不在凹凸面,双曲平面 - 凹随处可见,就像某种渠道或一个马鞍,只是无尽的。如何是球体的(曲率)的半径,并且在罗巴切夫斯基平面有一定的曲率测度。仅此曲率的范围是正的,而在平面罗巴切夫斯基 - 阴性
。
在一个非常小的规模,或者通过增加曲率,该几何形状是接近欧几里德罗巴切夫斯基。因此,这可能是因为我们生活在一个相当大的措施曲率Lobachevskii空间,所以在我们的规模不会注意到它。特别是,相对论它遵循质量在宇宙中均匀分布,我们的空间可能是双曲几何。如果这是这样,它可以被称为罗巴切夫斯基爱因斯坦数学。
今天是完全221年自尼古拉·伊万诺维奇·罗巴切夫斯基的诞生。从你和祝贺!
附: A“平行”线相交,在射影几何,但这是另一个故事。
资料来源:
你肯定听说过,在罗巴切夫斯基几何平行线相交。当然,这不是。甚至相反。
从学校的几何当然,我们知道,[以下简称尔冬升]“通过不就行了点,可以画出一条线平行的直线这一点,也是唯一一个»。
这种说法 - 最流行的意译欧几里得的第五公设,谁曾放置了一个沉重的猪他的追随者。在其“元素”前四个公设配方很浅显的事实。在这里,他们是:
1.从任何角度任何时候,你可以画一条直线[只有一]
2.限线可以连续保持在一条直线上。
3.在所有的每一个解决方案可谓是一个圆的中心。
4.所有的直角相等。
在第五公设欧几里得决定potrollit数学家,而是写一些简单的“矩形存在”(就是这样!),他开始迷惑:“如果一条直线相交的两条直线,使内部单向角......等等等等等等...“

每个人都认为:这是黑暗的这里,能不能成为这样一个复杂的公理。不承认的伎俩,数学2000年试图摆脱这个假设,并通过其他公设和公理证明这一点。起初,希腊人,然后是阿拉伯人,然后是欧洲人。每个人都认为他成功地证明了这个前提,但后来事实证明,证明是基于一些明显的,但不能证明该说法无异于推测。这种说法已经积累了巨大的集合。下面是其中一些:
1.有三角形任意大区
2.有相似三角形
3.一个三角形的内角之和为180°
4.勾股定理是真实的
5.圆周的直径之比 - 恒定并等于π
6.两行平行的第三是相互平行
最后一点,并起着罗巴切夫斯基的几何形状的混乱了关键作用。但在更多的后来。
最后,最先进的数学家开始尝试证据应用于相反[欧几里得] - 也就是说,我们假定第五公是不正确的,并从这个任何矛盾推断。首先是意大利Saccheri(第十八世纪上半叶),这是非常恼火,他不觉得这是一个矛盾。最后,他在计算中的错误,我们得到一个矛盾,并愉快地叹了口气。
渐渐地,数学家开始怀疑的东西。而尝试了放弃第五公设是不是找一对矛盾,但只是为了看看会发生什么。第一个成功实现兰伯特,在十八世纪下半叶谁。他建立在球体,其中三角形的内角之和总是大于180°,并且所有的线相交一致的几何形状。然而,在球面几何被干扰不仅是第五公而且至少前三。顺便说一下,所述第四静止已被证实,并排除在公设。
兰伯特还研究几何,其中三角形的内角之和总是小于180度,没有发现它的冲突,但无法想象这样乱说一个假想的球体。因此,他不追求这个问题,限制了说法,这是无法证明的第五公设。
在这个施韦卡特和高斯进一步的工作。高斯完全明白了一切,但他也知道什么擦这种古老的科学团体 - 我们自己的危险。 Zaminusili,则事能够发布。因此,他们都悄无声息自己变成一个管。
第一谁公开宣布非欧几何是罗巴切夫斯基。首先,在发表的一份报告于1826年,然后在1829年。当然,这一切下雨的颠簸,他几乎失去了他的岗位作为喀山大学校长。他被人误解和嘲笑,无论是在俄罗斯和国外。但是他继续坚持和立场,并移动到最远的几何形状的一项新的研究。且自那时起他的名字命名。
几乎像在歌曲唱:
一个值得信贷,一是应有的责任
而尼古拉·伊万诺维奇·罗巴切夫斯基是他的名字
无论罗巴切夫斯基,但三年后,他发表了他对非欧几何的工作,匈牙利数学家波尔约,也依然被忽视。
高斯赞赏罗巴切夫斯基的工作,但只有在私人信件。他甚至想学习俄语读他的俄语出版。 1860年(后死亡,高斯,和罗巴切夫斯基)高斯函授成为公众和有关罗巴切夫斯基好评如潮提请注意的俄罗斯科学家和他的想法。在一般情况下,正义得到了伸张,但一如既往追授。
所以,在通过相同的点的几何罗巴切夫斯基可以由至少两条直线平行于此,但一般是无限的。这似乎是一次平行线穿过一个点,它们相交。是的,它们重叠,但诀窍是它们不彼此平行,尽管这两个平行的第三线。
再说,当你可能猜到,一个三角形的内角之和总是小于180°时,通过圆周的恒定比率一定到与圆等的直径增加的三角形的面积这样的东西。而勾股定理是行不通的。
如何提出一个表面罗巴切夫斯基几何上的工作?在这里,它是 - 在KDPV,有一个非常性感的她一个三角形。这个所谓双曲平面。如果球 - 无处不在凹凸面,双曲平面 - 凹随处可见,就像某种渠道或一个马鞍,只是无尽的。如何是球体的(曲率)的半径,并且在罗巴切夫斯基平面有一定的曲率测度。仅此曲率的范围是正的,而在平面罗巴切夫斯基 - 阴性
。
在一个非常小的规模,或者通过增加曲率,该几何形状是接近欧几里德罗巴切夫斯基。因此,这可能是因为我们生活在一个相当大的措施曲率Lobachevskii空间,所以在我们的规模不会注意到它。特别是,相对论它遵循质量在宇宙中均匀分布,我们的空间可能是双曲几何。如果这是这样,它可以被称为罗巴切夫斯基爱因斯坦数学。
今天是完全221年自尼古拉·伊万诺维奇·罗巴切夫斯基的诞生。从你和祝贺!
附: A“平行”线相交,在射影几何,但这是另一个故事。
资料来源: