506
Перерва на постули
Автор irygaev
Ви, мабуть, чули, що в Лобачевській геометрії паралельні лінії міжсекти. Звичайно це не так. І навпаки.
Від шкільного курсу геометрії ми знаємо, що «прорив точки, яка не лягає на прямій лінії, можна зробити пряму лінію паралельно цьому, і тільки один. й
Ця заява є найпопулярнішим парафразом п'ятого постули Euclid, який в один раз уклала велику свиню до його послідовників. Цей факт полягає в тому, що в його елементах перші чотири листи сформульовані дуже просто і чітко. Ось вони:
1,1 км З кожної точки до кожної точки ви можете намалювати пряму лінію.
2,2 км Лінійка може бути безперервно продовжена в прямій лінії.
3. У З будь-якого центру можна описати будь-яким розчином.
4. У Всі праві кути рівні один одному.
У п'ятому постулі Euclid вирішив прогулятися математиками, а замість написання щось так просто, як «Ректкутники існують» (і база!), він почав плутати: «Якщо прямі лінії перетинають дві прямі лінії формують внутрішні односторонні кути ... blah blah blah blah blah blah blah blah blah blah blah blah blah ...»
І кожен думав: щось темне тут, тут не можна осями так комплексно. Без визнання лову, математику за 2000 років спробували позбутися від цього постули і довести її через інші постули і аксіоми. Перші давньогреки, потім Араби, потім європейці. І кожен думав, що він успішно зарекомендував цю поставу, але потім виявилося, що його доказ було засновано на певній очевидній, але непровансій заяві, еквівалентній поставу. Є багато таких претензій. Ось ще:
1,1 км Є трикутники довільно велика площа
2,2 км Є трикутники, як це.
3. У Сума кутів трикутника 180°
4. теорема Пітагораса правильно
5. Умань Співвідношення окружності до діаметру постійно і дорівнює π
6. Жнівень Два лінії паралельно третій паралельно один одному.
Остання точка грає ключову роль у зборі з геометрією Лобачевського. А ще далі.
І, нарешті, найбільш просунуті математики почали намагатися застосувати доказ навпаки, тобто припустити, що п'ятий постул невірний, і вивести деякі протиріччя від нього. Першим був італійський Сакчері (перша половина вісімнадцятого століття), який дуже дратував, що він не міг знайти цей протиріччя. В кінці він зробив помилку в своїх підрахунках, отримав суперечність, і зважився щасливо.
Мало мало, математики почали підозрювати щось. Атемпти вже почали відмовитися від п'ятого поставу, щоб не знайти протиріччя, але просто побачити, що відбувається. Перші успіхи були досягнуті Ламбертом, які в другій половині XVIII століття звели послідовну геометрію на сферу, в якій сума кутів трикутника завжди перевищує 180° і всі прямі лінії міжсектичними. Однак в сферичній геометрії порушується не тільки п'ятий постул, але хоча б перші три. До речі, четверта була доведена і виключена з постулів.
Ламберт також досліджував геометрію, в якій сума кутів трикутника завжди менше 180°, не знайдено суперечок в ній, але не змогли уявити таку явну сферу. Тому він не розвив тему, обмежуючи себе заявою, що неможливо довести п'ятий постул.
На ній працювала Schweickart і Gauss. Зрозуміло, але він також зрозумів, що розтирання такої венозної наукової громади коштує дорожче. Не пропустіть вас, а потім ви не зможете розмістити щось. Так вони тихо зберігають свою ротову затвору.
Перший публічно декларувати не-Еуклідену геометрію був Лобачевським. Перший у звіті 1826 р., потім у публікації 1829 р. Природно, всі бампи припав на нього, і він практично втратив посаду ректора Казанського університету. Він був непідступним і безглуздим, як в Росії, так і за кордоном. Але він продовжував наполягати і захищати, і просунувся далі в дослідженні нової геометрії. І з тих пір він був названий ним.
Майже подобається пісня говорить:
Одне заслуговує на кредит, заслуговує блюм
І Микола Іванович Лобачевський - його ім'я
Незалежно від Лобачевського, але через три роки угорська математика Бойа публікує папір на неевклідну геометрію, яка також йде неочікувано.
Гаусс хвалі Робота Лобачевського, але тільки в особистому листуванні. Він навіть спробував дізнатися російську мову, щоб читати його російськомовні видання. У 1860-ті роки (після смерті обох Гаусів і Лобачевського), лист Гауса став громадським, а його захоплені відгуки Лобачевського звернулися до російського вченого і його ідей. В цілому, справедливість переважала, але як завжди посмертно.
Отже, в геометрії Лобачевського, хоча б два лінії паралельно цьому можна тягнути через одну точку, а в цілому, нескінченно багато. Здавалося б, якщо паралельні лінії проходять через одну точку, вони перетинаються. Так, вони перекриваються, але хитрість полягає в тому, що вони не паралельно один одному, хоча обидва паралельні третій лінії.
А крім того, як ви напевно вгадаєте, сума кутів трикутника завжди менше 180 °, площа трикутника обмежена констанцією, співвідношення окружності до діаметра збільшується з збільшенням окружності і т.д. Що таке. А теорема Пилипа не працює.
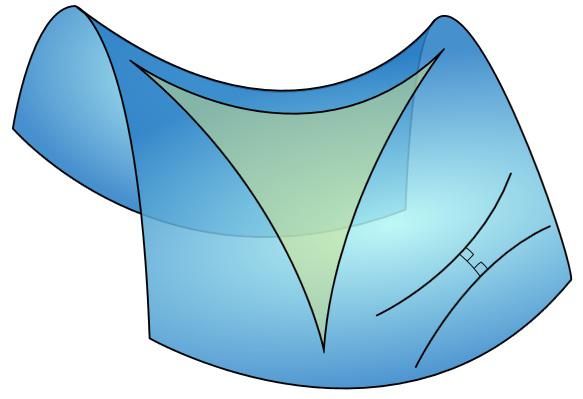
Як ми можемо уявити поверхню, на якій працює геометрія Лобачевського? І ось вона на CDPV, з дуже сексуальним трикутником на ній. Це так званий гіперболічний літак. Якщо сфера є конвекційною поверхнею всюди, то гіперболічна площина всюди закріплюється, як деякі воронки або сідла, тільки нескінченні. Як сфера має радіус (викривлення), тому площина Лобачевського має певну показник викривлення. Тільки у сфері ця кривизня позитивна, а в площині Лобачевського це негативно.
На дуже невеликому масштабі або при збільшенні кривизни, геометрія Лобачевського наближається геометрія Euclidean. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. Зокрема, це випливає з теорії релятивності, що, враховуючи рівномірний розподіл маси в Всесвіті, наш простір може добре мати геометрію Лобачевського. Якщо це виявиться вірним, то Лобачевський можна назвати Ейнштейном математики.
Сьогодні відзначає 221 річницю від дня народження Миколая Івановича Лобачевського. Вітаємо!
П.С. Паралельні лінії міжсектичними геометрією, але це ще одна історія.
Джерело:
Ви, мабуть, чули, що в Лобачевській геометрії паралельні лінії міжсекти. Звичайно це не так. І навпаки.
Від шкільного курсу геометрії ми знаємо, що «прорив точки, яка не лягає на прямій лінії, можна зробити пряму лінію паралельно цьому, і тільки один. й
Ця заява є найпопулярнішим парафразом п'ятого постули Euclid, який в один раз уклала велику свиню до його послідовників. Цей факт полягає в тому, що в його елементах перші чотири листи сформульовані дуже просто і чітко. Ось вони:
1,1 км З кожної точки до кожної точки ви можете намалювати пряму лінію.
2,2 км Лінійка може бути безперервно продовжена в прямій лінії.
3. У З будь-якого центру можна описати будь-яким розчином.
4. У Всі праві кути рівні один одному.
У п'ятому постулі Euclid вирішив прогулятися математиками, а замість написання щось так просто, як «Ректкутники існують» (і база!), він почав плутати: «Якщо прямі лінії перетинають дві прямі лінії формують внутрішні односторонні кути ... blah blah blah blah blah blah blah blah blah blah blah blah blah ...»

І кожен думав: щось темне тут, тут не можна осями так комплексно. Без визнання лову, математику за 2000 років спробували позбутися від цього постули і довести її через інші постули і аксіоми. Перші давньогреки, потім Араби, потім європейці. І кожен думав, що він успішно зарекомендував цю поставу, але потім виявилося, що його доказ було засновано на певній очевидній, але непровансій заяві, еквівалентній поставу. Є багато таких претензій. Ось ще:
1,1 км Є трикутники довільно велика площа
2,2 км Є трикутники, як це.
3. У Сума кутів трикутника 180°
4. теорема Пітагораса правильно
5. Умань Співвідношення окружності до діаметру постійно і дорівнює π
6. Жнівень Два лінії паралельно третій паралельно один одному.
Остання точка грає ключову роль у зборі з геометрією Лобачевського. А ще далі.
І, нарешті, найбільш просунуті математики почали намагатися застосувати доказ навпаки, тобто припустити, що п'ятий постул невірний, і вивести деякі протиріччя від нього. Першим був італійський Сакчері (перша половина вісімнадцятого століття), який дуже дратував, що він не міг знайти цей протиріччя. В кінці він зробив помилку в своїх підрахунках, отримав суперечність, і зважився щасливо.
Мало мало, математики почали підозрювати щось. Атемпти вже почали відмовитися від п'ятого поставу, щоб не знайти протиріччя, але просто побачити, що відбувається. Перші успіхи були досягнуті Ламбертом, які в другій половині XVIII століття звели послідовну геометрію на сферу, в якій сума кутів трикутника завжди перевищує 180° і всі прямі лінії міжсектичними. Однак в сферичній геометрії порушується не тільки п'ятий постул, але хоча б перші три. До речі, четверта була доведена і виключена з постулів.
Ламберт також досліджував геометрію, в якій сума кутів трикутника завжди менше 180°, не знайдено суперечок в ній, але не змогли уявити таку явну сферу. Тому він не розвив тему, обмежуючи себе заявою, що неможливо довести п'ятий постул.
На ній працювала Schweickart і Gauss. Зрозуміло, але він також зрозумів, що розтирання такої венозної наукової громади коштує дорожче. Не пропустіть вас, а потім ви не зможете розмістити щось. Так вони тихо зберігають свою ротову затвору.
Перший публічно декларувати не-Еуклідену геометрію був Лобачевським. Перший у звіті 1826 р., потім у публікації 1829 р. Природно, всі бампи припав на нього, і він практично втратив посаду ректора Казанського університету. Він був непідступним і безглуздим, як в Росії, так і за кордоном. Але він продовжував наполягати і захищати, і просунувся далі в дослідженні нової геометрії. І з тих пір він був названий ним.
Майже подобається пісня говорить:
Одне заслуговує на кредит, заслуговує блюм
І Микола Іванович Лобачевський - його ім'я
Незалежно від Лобачевського, але через три роки угорська математика Бойа публікує папір на неевклідну геометрію, яка також йде неочікувано.
Гаусс хвалі Робота Лобачевського, але тільки в особистому листуванні. Він навіть спробував дізнатися російську мову, щоб читати його російськомовні видання. У 1860-ті роки (після смерті обох Гаусів і Лобачевського), лист Гауса став громадським, а його захоплені відгуки Лобачевського звернулися до російського вченого і його ідей. В цілому, справедливість переважала, але як завжди посмертно.
Отже, в геометрії Лобачевського, хоча б два лінії паралельно цьому можна тягнути через одну точку, а в цілому, нескінченно багато. Здавалося б, якщо паралельні лінії проходять через одну точку, вони перетинаються. Так, вони перекриваються, але хитрість полягає в тому, що вони не паралельно один одному, хоча обидва паралельні третій лінії.
А крім того, як ви напевно вгадаєте, сума кутів трикутника завжди менше 180 °, площа трикутника обмежена констанцією, співвідношення окружності до діаметра збільшується з збільшенням окружності і т.д. Що таке. А теорема Пилипа не працює.
Як ми можемо уявити поверхню, на якій працює геометрія Лобачевського? І ось вона на CDPV, з дуже сексуальним трикутником на ній. Це так званий гіперболічний літак. Якщо сфера є конвекційною поверхнею всюди, то гіперболічна площина всюди закріплюється, як деякі воронки або сідла, тільки нескінченні. Як сфера має радіус (викривлення), тому площина Лобачевського має певну показник викривлення. Тільки у сфері ця кривизня позитивна, а в площині Лобачевського це негативно.
На дуже невеликому масштабі або при збільшенні кривизни, геометрія Лобачевського наближається геометрія Euclidean. Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. Зокрема, це випливає з теорії релятивності, що, враховуючи рівномірний розподіл маси в Всесвіті, наш простір може добре мати геометрію Лобачевського. Якщо це виявиться вірним, то Лобачевський можна назвати Ейнштейном математики.
Сьогодні відзначає 221 річницю від дня народження Миколая Івановича Лобачевського. Вітаємо!
П.С. Паралельні лінії міжсектичними геометрією, але це ще одна історія.
Джерело: