498
0.1
2015-07-04
Слом постулатов
Автор irygaev
Наверняка вы когда–нибудь слышали, что в геометрии Лобачевского параллельные прямые пересекаются. Конечно же, это не так. И даже наоборот.
Из школьного курса геометрии мы знаем, что [далее менторским тоном] «через точку, не лежащую на прямой, можно провести прямую, параллельную данной, и только одну».
Это утверждение – наиболее популярное перефразирование пятого постулата Евклида, который в своё время подложил здоровенную свинью своим последователям. Дело в том, что в его «Началах» первые четыре постулата сформулированы очень просто и очевидно. Вот они:
1. От всякой точки до всякой точки можно провести прямую [и только одну]
2. Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким раствором может быть описан круг.
4. Все прямые углы равны между собой.
В пятом же постулате Евклид решил потроллить математиков, и вместо того, чтобы написать что–нибудь столь же простое, например, «Прямоугольники существуют» (и баста!), он начал запутывать: «Если прямая, пересекающая две прямые, образует внутренние односторонние углы… бла–бла–бла…»
И все подумали: что–то он здесь темнит, не может быть аксиома такой сложной. Не распознав подвох, математики в течение 2 тысяч лет пытались избавиться от этого постулата и доказать его через другие постулаты и аксиомы. Сначала древние греки, потом арабы, потом европейцы. И каждый думал, что он успешно доказал этот постулат, но потом выяснялось, что его доказательство базируется на каком–нибудь очевидном, но не доказанном утверждении, равнозначном самому постулату. Таких утверждений набралось огромное множество. Вот ещё некоторые из них:
1. Существуют треугольники сколь угодно большой площади
2. Существуют подобные треугольники
3. Сумма углов треугольник равна 180°
4. Теорема Пифагора верна
5. Отношение длины окружности к диаметру – константа и равно π
6. Две прямые, параллельные третьей, параллельны друг другу
Последний пункт и играет ключевую роль в путанице с геометрией Лобачевского. Но об этом чуть позже.
Наконец, наиболее продвинутые из математиков стали пытаться применить доказательство от противного[Евклида] – то есть, предположить, что пятый постулат не верен, и вывести из этого какое–нибудь противоречие. Первым был итальянец Саккери (первая половина XVIII в.), который очень досадовал, что никак не может найти это противоречие. В конце концов, он сделал ошибку в вычислениях, получил противоречие и радостно вздохнул.
Мало–помалу математики стали что–то подозревать. И уже начались попытки отказаться от пятого постулата не в целях найти противоречие, а просто посмотреть, что же получится. Первых успехов добился Ламберт, который во второй половине XVIII в. построил непротиворечивую геометрию на сфере, в которой сумма углов треугольника всегда больше 180° и все прямые пересекаются. Однако в сферической геометрии нарушается не только пятый постулат, но и как минимум первые три. Кстати, четвёртый всё–таки был доказан и исключен из постулатов.
Ламберт также исследовал геометрию, в которой сумма углов треугольника всегда меньше 180°, не нашёл в ней противоречий, но не смог представить себе этакую мнимую сферу. Поэтому он не стал развивать тему, ограничившись заявлением, что доказать пятый постулат невозможно.
Дальше над этим работали Швейкарт и Гаусс. Гаусс отлично всё понимал, но понимал также и то, что втирать подобное почтенному научному сообществу – себе дороже. Заминусуют, потом вообще ничего не сможешь постить. Поэтому они оба тихо молчали себе в трубочку.
Первым, кто во всеуслышание заявил о неевклидовой геометрии, был Лобачевский. Сначала в докладе в 1826 году, затем в публикации 1829 года. Естественно на него посыпались все шишки, и он чуть было не лишился поста ректора Казанского университета. Он был не понят и осмеян, как в России, так и за рубежом. Но продолжал настаивать и отстаивать, и продвинулся в исследовании новой геометрии дальше всех. И с тех пор она носит его имя.
Почти как в песне поётся:
One deserves the credit, one deserves the blame
And Nikolai Ivanovich Lobachevsky is his name
Независимо от Лобачевского, но на три года позже него, публикует работу о неевклидовой геометрии венгерский математик Бойяи, которая также остаётся незамеченной.
Гаусс высоко оценивал работу Лобачевского, но только в частной переписке. Он даже пытался учить русский язык, чтобы почитать его русскоязычные публикации. В 1860–х годах (уже после смерти и Гаусса, и Лобачевского) переписка Гаусса становится достоянием общественности, и его восторженные отзывы о Лобачевском привлекают внимание к русскому учёному и его идеям. В общем, справедливость восторжествовала, но как всегда посмертно.
Итак, в геометрии Лобачевского через одну точку можно провести как минимум две прямые, параллельные данной, а вообще бесконечно много. Казалось бы, раз параллельные прямые проходят через одну точку, то они пересекаются. Да, они пересекаются, но фокус в том, что они не параллельны друг другу, хоть обе параллельны третьей прямой.
Ну и кроме этого, как вы, наверное, догадываетесь, сумма углов треугольника всегда меньше 180°, площадь треугольника ограничена константой, отношение длины окружности к диаметру растёт с увеличением окружности и т.д. Всё в таком духе. Да и теорема Пифагора не работает.
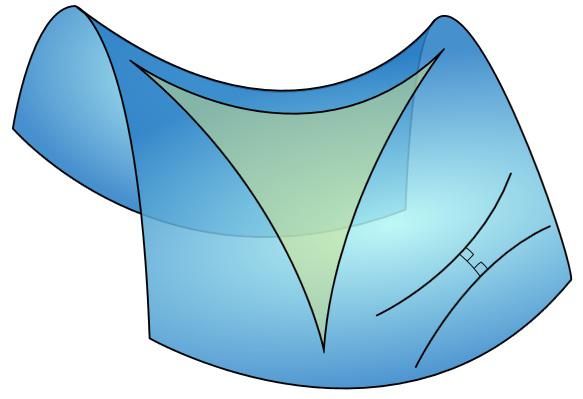
Как же представить такую поверхность, на которой работает геометрия Лобачевского? А вот она – на КДПВ, с очень сексуальным треугольничком на ней. Это так называемая гиперболическая плоскость. Если сфера – повсюду выпуклая поверхность, то гиперболическая плоскость – повсюду вогнутая, как какая–нибудь воронка или седло, только бесконечная. Как у сферы есть радиус (кривизны), так и у плоскости Лобачевского есть некий показатель кривизны. Только у сферы эта кривизна положительна, а у плоскости Лобачевского – отрицательна.
На очень маленьком масштабе, либо при увеличении показателя кривизны, геометрия Лобачевского приближается к евклидовой. Так что, вполне может оказаться, что мы живём в пространстве Лобачевского с достаточно большим показателем кривизны, поэтому не замечаем этого в наших масштабах. В частности, из теории относительности следует, что при равномерном распределении массы во вселенной, наше пространство вполне может иметь геометрию Лобачевского. Если это действительно окажется так, то Лобачевского можно назвать Эйнштейном математики.
А сегодня как раз исполняется 221 год со дня рождения Николая Ивановича Лобачевского. С чем вас и поздравляю!
P.S. А «параллельные» прямые пересекаются в проективной геометрии, но это уже совсем другая история.
Источник: www.yaplakal.com/
Наверняка вы когда–нибудь слышали, что в геометрии Лобачевского параллельные прямые пересекаются. Конечно же, это не так. И даже наоборот.
Из школьного курса геометрии мы знаем, что [далее менторским тоном] «через точку, не лежащую на прямой, можно провести прямую, параллельную данной, и только одну».
Это утверждение – наиболее популярное перефразирование пятого постулата Евклида, который в своё время подложил здоровенную свинью своим последователям. Дело в том, что в его «Началах» первые четыре постулата сформулированы очень просто и очевидно. Вот они:
1. От всякой точки до всякой точки можно провести прямую [и только одну]
2. Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким раствором может быть описан круг.
4. Все прямые углы равны между собой.
В пятом же постулате Евклид решил потроллить математиков, и вместо того, чтобы написать что–нибудь столь же простое, например, «Прямоугольники существуют» (и баста!), он начал запутывать: «Если прямая, пересекающая две прямые, образует внутренние односторонние углы… бла–бла–бла…»

И все подумали: что–то он здесь темнит, не может быть аксиома такой сложной. Не распознав подвох, математики в течение 2 тысяч лет пытались избавиться от этого постулата и доказать его через другие постулаты и аксиомы. Сначала древние греки, потом арабы, потом европейцы. И каждый думал, что он успешно доказал этот постулат, но потом выяснялось, что его доказательство базируется на каком–нибудь очевидном, но не доказанном утверждении, равнозначном самому постулату. Таких утверждений набралось огромное множество. Вот ещё некоторые из них:
1. Существуют треугольники сколь угодно большой площади
2. Существуют подобные треугольники
3. Сумма углов треугольник равна 180°
4. Теорема Пифагора верна
5. Отношение длины окружности к диаметру – константа и равно π
6. Две прямые, параллельные третьей, параллельны друг другу
Последний пункт и играет ключевую роль в путанице с геометрией Лобачевского. Но об этом чуть позже.
Наконец, наиболее продвинутые из математиков стали пытаться применить доказательство от противного[Евклида] – то есть, предположить, что пятый постулат не верен, и вывести из этого какое–нибудь противоречие. Первым был итальянец Саккери (первая половина XVIII в.), который очень досадовал, что никак не может найти это противоречие. В конце концов, он сделал ошибку в вычислениях, получил противоречие и радостно вздохнул.
Мало–помалу математики стали что–то подозревать. И уже начались попытки отказаться от пятого постулата не в целях найти противоречие, а просто посмотреть, что же получится. Первых успехов добился Ламберт, который во второй половине XVIII в. построил непротиворечивую геометрию на сфере, в которой сумма углов треугольника всегда больше 180° и все прямые пересекаются. Однако в сферической геометрии нарушается не только пятый постулат, но и как минимум первые три. Кстати, четвёртый всё–таки был доказан и исключен из постулатов.
Ламберт также исследовал геометрию, в которой сумма углов треугольника всегда меньше 180°, не нашёл в ней противоречий, но не смог представить себе этакую мнимую сферу. Поэтому он не стал развивать тему, ограничившись заявлением, что доказать пятый постулат невозможно.
Дальше над этим работали Швейкарт и Гаусс. Гаусс отлично всё понимал, но понимал также и то, что втирать подобное почтенному научному сообществу – себе дороже. Заминусуют, потом вообще ничего не сможешь постить. Поэтому они оба тихо молчали себе в трубочку.
Первым, кто во всеуслышание заявил о неевклидовой геометрии, был Лобачевский. Сначала в докладе в 1826 году, затем в публикации 1829 года. Естественно на него посыпались все шишки, и он чуть было не лишился поста ректора Казанского университета. Он был не понят и осмеян, как в России, так и за рубежом. Но продолжал настаивать и отстаивать, и продвинулся в исследовании новой геометрии дальше всех. И с тех пор она носит его имя.
Почти как в песне поётся:
One deserves the credit, one deserves the blame
And Nikolai Ivanovich Lobachevsky is his name
Независимо от Лобачевского, но на три года позже него, публикует работу о неевклидовой геометрии венгерский математик Бойяи, которая также остаётся незамеченной.
Гаусс высоко оценивал работу Лобачевского, но только в частной переписке. Он даже пытался учить русский язык, чтобы почитать его русскоязычные публикации. В 1860–х годах (уже после смерти и Гаусса, и Лобачевского) переписка Гаусса становится достоянием общественности, и его восторженные отзывы о Лобачевском привлекают внимание к русскому учёному и его идеям. В общем, справедливость восторжествовала, но как всегда посмертно.
Итак, в геометрии Лобачевского через одну точку можно провести как минимум две прямые, параллельные данной, а вообще бесконечно много. Казалось бы, раз параллельные прямые проходят через одну точку, то они пересекаются. Да, они пересекаются, но фокус в том, что они не параллельны друг другу, хоть обе параллельны третьей прямой.
Ну и кроме этого, как вы, наверное, догадываетесь, сумма углов треугольника всегда меньше 180°, площадь треугольника ограничена константой, отношение длины окружности к диаметру растёт с увеличением окружности и т.д. Всё в таком духе. Да и теорема Пифагора не работает.
Как же представить такую поверхность, на которой работает геометрия Лобачевского? А вот она – на КДПВ, с очень сексуальным треугольничком на ней. Это так называемая гиперболическая плоскость. Если сфера – повсюду выпуклая поверхность, то гиперболическая плоскость – повсюду вогнутая, как какая–нибудь воронка или седло, только бесконечная. Как у сферы есть радиус (кривизны), так и у плоскости Лобачевского есть некий показатель кривизны. Только у сферы эта кривизна положительна, а у плоскости Лобачевского – отрицательна.
На очень маленьком масштабе, либо при увеличении показателя кривизны, геометрия Лобачевского приближается к евклидовой. Так что, вполне может оказаться, что мы живём в пространстве Лобачевского с достаточно большим показателем кривизны, поэтому не замечаем этого в наших масштабах. В частности, из теории относительности следует, что при равномерном распределении массы во вселенной, наше пространство вполне может иметь геометрию Лобачевского. Если это действительно окажется так, то Лобачевского можно назвать Эйнштейном математики.
А сегодня как раз исполняется 221 год со дня рождения Николая Ивановича Лобачевского. С чем вас и поздравляю!
P.S. А «параллельные» прямые пересекаются в проективной геометрии, но это уже совсем другая история.
Источник: www.yaplakal.com/
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.