505
Scrapping postulates
Author irygaev
Surely you've ever heard of that in Lobachevsky geometry parallel lines intersect. Of course, it is not. And even on the contrary.
From school geometry course, we know that [hereinafter didactic tone] "through a point not on the line, you can draw a straight line parallel to this, and the only one».
This statement - the most popular paraphrase Euclid's fifth postulate, who once placed a hefty pig to his followers. The fact that in its "Elements" first four postulates formulated very simple and obvious. Here they are:
1. From any point to any point you can draw a straight line [and only one]
2. Restricted line can be continuously keep in a straight line.
3. Of all the center every solution can be described as a circle.
4. All right angles are equal.
In the fifth postulate Euclid decided potrollit mathematicians, and instead write something as simple as, "Rectangles exist" (and that's that!), He began to confuse: "If a straight line intersects two straight lines makes the interior one-way corners ... blah blah blah ... »
And everyone thought: is it dark in here, can not be an axiom of such a complex. Does not recognize the trick, mathematics for 2 thousand years trying to get rid of this postulate and prove it through other postulates and axioms. At first the Greeks and then the Arabs and then the Europeans. And everyone thought he successfully proved this premise, but then it turned out that the proof is based on some obvious, but do not prove the assertion is tantamount to postulate. Such claims had accumulated huge set. Here are some of them:
1. There triangles arbitrarily large area
2. There are similar triangles
3. The sum of the angles of a triangle is 180 °
4. The Pythagorean theorem is true
5. The ratio of the circumference to the diameter - constant and equal to π
6. Two lines parallel to a third are parallel to each other
The last point, and plays a key role in the confusion of the geometry of Lobachevsky. But more on that later.
Finally, the most advanced mathematicians began to try to apply the evidence to the contrary [Euclid] - that is, we assume that the fifth postulate is not true, and deduce from this any contradiction. The first was an Italian Saccheri (first half of the XVIII century.), Which is very annoyed that he could not find it a contradiction. In the end, he made a mistake in calculations, we get a contradiction, and sighed happily.
Little by little, mathematicians began to suspect something. And attempts were made to give up the fifth postulate is not to find a contradiction, but just to see what happens. The first success achieved Lambert, who in the second half of the XVIII century. He built a consistent geometry on the sphere, in which the sum of the angles of a triangle is always greater than 180 ° and all the lines intersect. However, in the spherical geometry is disturbed not only the fifth postulate but also at least the first three. By the way, the fourth still has been proven and is excluded from the postulates.
Lambert also studied geometry in which the sum of the angles of a triangle is always less than 180 °, did not find it in conflict, but could not imagine such utter an imaginary sphere. Therefore, he did not pursue the subject, limiting the statement that it is impossible to prove the fifth postulate.
Further work on this Schweickart and Gauss. Gauss perfectly understood everything, but he knew also what to rub such venerable scientific community - our own peril. Zaminusili, then nothing will be able to post. Therefore they are both quiet silence itself into a tube.
The first who publicly declared non-Euclidean geometry was Lobachevsky. First, in a report in 1826, then in 1829 in the publication. Of course it rained all the bumps, and he almost lost his post as rector of Kazan University. He was misunderstood and ridiculed, both in Russia and abroad. But he continued to insist and stand, and moved to a new study of the geometry of the farthest. And since then it bears his name.
Almost like in the song is sung:
One deserves the credit, one deserves the blame
And Nikolai Ivanovich Lobachevsky is his name
Regardless of Lobachevsky, but three years later he publishes his work on non-Euclidean geometry, Hungarian mathematician Bolyai, also remains unnoticed.
Gauss appreciated the work of Lobachevsky, but only in private correspondence. He even tried to learn Russian to read his Russian-language publication. In 1860 (after the death and Gauss, and Lobachevsky) Gauss correspondence becomes public, and rave reviews about Lobachevsky draw attention to the Russian scientist and his ideas. In general, justice has been done, but as always posthumously.
So, in the Lobachevsky geometry through the same point can be made at least two straight lines parallel to this, but in general infinite. It would seem that once parallel lines pass through one point, they intersect. Yes, they overlap, but the trick is that they are not parallel to each other, though the two are parallel to a third line.
And besides, as you probably guessed, the sum of the angles of a triangle is always less than 180 °, the area of the triangle bounded by a constant ratio of the circumference to the diameter increases with the circle, etc. Stuff like that. And the Pythagorean theorem is not working.
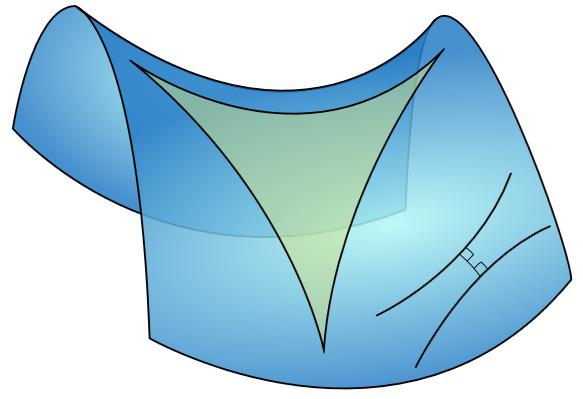
How to present a surface on which the work of Lobachevsky geometry? And here it is - on KDPV, a triangle with a very sexy on her. This so-called hyperbolic plane. If the sphere - everywhere convex surface, the hyperbolic plane - concave everywhere, like some kind of a funnel or a saddle, just endless. How is the radius of the sphere at (curvature), and at the Lobachevsky plane there is a certain measure of curvature. Only the scope of this curvature is positive, and in the Lobachevsky plane - negative.
On a very small scale, or by increasing the curvature, the geometry is close to Euclidean Lobachevsky. So, it may be that we live in a Lobachevskii space with a fairly large measure of curvature, so do not notice it at our scale. In particular, the theory of relativity it follows that a uniform distribution of mass in the universe, our space may be hyperbolic geometry. Should this be so, it can be called Lobachevsky Einstein mathematics.
Today marks exactly 221 years since the birth of Nikolai Ivanovich Lobachevsky. From what you and congratulations!
P.S. A "parallel" lines intersect in the projective geometry, but that's another story.
Source:
Surely you've ever heard of that in Lobachevsky geometry parallel lines intersect. Of course, it is not. And even on the contrary.
From school geometry course, we know that [hereinafter didactic tone] "through a point not on the line, you can draw a straight line parallel to this, and the only one».
This statement - the most popular paraphrase Euclid's fifth postulate, who once placed a hefty pig to his followers. The fact that in its "Elements" first four postulates formulated very simple and obvious. Here they are:
1. From any point to any point you can draw a straight line [and only one]
2. Restricted line can be continuously keep in a straight line.
3. Of all the center every solution can be described as a circle.
4. All right angles are equal.
In the fifth postulate Euclid decided potrollit mathematicians, and instead write something as simple as, "Rectangles exist" (and that's that!), He began to confuse: "If a straight line intersects two straight lines makes the interior one-way corners ... blah blah blah ... »

And everyone thought: is it dark in here, can not be an axiom of such a complex. Does not recognize the trick, mathematics for 2 thousand years trying to get rid of this postulate and prove it through other postulates and axioms. At first the Greeks and then the Arabs and then the Europeans. And everyone thought he successfully proved this premise, but then it turned out that the proof is based on some obvious, but do not prove the assertion is tantamount to postulate. Such claims had accumulated huge set. Here are some of them:
1. There triangles arbitrarily large area
2. There are similar triangles
3. The sum of the angles of a triangle is 180 °
4. The Pythagorean theorem is true
5. The ratio of the circumference to the diameter - constant and equal to π
6. Two lines parallel to a third are parallel to each other
The last point, and plays a key role in the confusion of the geometry of Lobachevsky. But more on that later.
Finally, the most advanced mathematicians began to try to apply the evidence to the contrary [Euclid] - that is, we assume that the fifth postulate is not true, and deduce from this any contradiction. The first was an Italian Saccheri (first half of the XVIII century.), Which is very annoyed that he could not find it a contradiction. In the end, he made a mistake in calculations, we get a contradiction, and sighed happily.
Little by little, mathematicians began to suspect something. And attempts were made to give up the fifth postulate is not to find a contradiction, but just to see what happens. The first success achieved Lambert, who in the second half of the XVIII century. He built a consistent geometry on the sphere, in which the sum of the angles of a triangle is always greater than 180 ° and all the lines intersect. However, in the spherical geometry is disturbed not only the fifth postulate but also at least the first three. By the way, the fourth still has been proven and is excluded from the postulates.
Lambert also studied geometry in which the sum of the angles of a triangle is always less than 180 °, did not find it in conflict, but could not imagine such utter an imaginary sphere. Therefore, he did not pursue the subject, limiting the statement that it is impossible to prove the fifth postulate.
Further work on this Schweickart and Gauss. Gauss perfectly understood everything, but he knew also what to rub such venerable scientific community - our own peril. Zaminusili, then nothing will be able to post. Therefore they are both quiet silence itself into a tube.
The first who publicly declared non-Euclidean geometry was Lobachevsky. First, in a report in 1826, then in 1829 in the publication. Of course it rained all the bumps, and he almost lost his post as rector of Kazan University. He was misunderstood and ridiculed, both in Russia and abroad. But he continued to insist and stand, and moved to a new study of the geometry of the farthest. And since then it bears his name.
Almost like in the song is sung:
One deserves the credit, one deserves the blame
And Nikolai Ivanovich Lobachevsky is his name
Regardless of Lobachevsky, but three years later he publishes his work on non-Euclidean geometry, Hungarian mathematician Bolyai, also remains unnoticed.
Gauss appreciated the work of Lobachevsky, but only in private correspondence. He even tried to learn Russian to read his Russian-language publication. In 1860 (after the death and Gauss, and Lobachevsky) Gauss correspondence becomes public, and rave reviews about Lobachevsky draw attention to the Russian scientist and his ideas. In general, justice has been done, but as always posthumously.
So, in the Lobachevsky geometry through the same point can be made at least two straight lines parallel to this, but in general infinite. It would seem that once parallel lines pass through one point, they intersect. Yes, they overlap, but the trick is that they are not parallel to each other, though the two are parallel to a third line.
And besides, as you probably guessed, the sum of the angles of a triangle is always less than 180 °, the area of the triangle bounded by a constant ratio of the circumference to the diameter increases with the circle, etc. Stuff like that. And the Pythagorean theorem is not working.
How to present a surface on which the work of Lobachevsky geometry? And here it is - on KDPV, a triangle with a very sexy on her. This so-called hyperbolic plane. If the sphere - everywhere convex surface, the hyperbolic plane - concave everywhere, like some kind of a funnel or a saddle, just endless. How is the radius of the sphere at (curvature), and at the Lobachevsky plane there is a certain measure of curvature. Only the scope of this curvature is positive, and in the Lobachevsky plane - negative.
On a very small scale, or by increasing the curvature, the geometry is close to Euclidean Lobachevsky. So, it may be that we live in a Lobachevskii space with a fairly large measure of curvature, so do not notice it at our scale. In particular, the theory of relativity it follows that a uniform distribution of mass in the universe, our space may be hyperbolic geometry. Should this be so, it can be called Lobachevsky Einstein mathematics.
Today marks exactly 221 years since the birth of Nikolai Ivanovich Lobachevsky. From what you and congratulations!
P.S. A "parallel" lines intersect in the projective geometry, but that's another story.
Source: