Desguace postulados

Autor irygaev
Seguramente alguna vez has oído hablar de que en la geometría Lobachevsky líneas paralelas se cruzan. Por supuesto, no lo es. E incluso al contrario.

De curso de geometría de la escuela, sabemos que [el tono en adelante didáctica] "a través de un punto no en la línea, se puede trazar una línea recta paralela a esta, y el único».

Esta declaración - el más popular paráfrasis quinto postulado de Euclides, que una vez colocó un cerdo fuerte para sus seguidores. El hecho de que en sus "Elementos" primeros cuatro postulados formula muy simple y obvio. Aquí están:

1. Desde cualquier punto a cualquier punto se puede trazar una línea recta [y sólo uno]
2. Línea restringido se puede mantener de forma continua en una línea recta.
3. De todo el centro de cada solución puede ser descrito como un círculo.
4. Todos los ángulos rectos son iguales.

En el quinto postulado de Euclides decidió matemáticos potrollit, y en lugar de escribir algo tan simple como, "existen rectángulos" (y eso es todo!), Comenzó a confundir: "Si una línea recta intersecta dos rectas hace que el interior de un solo sentido esquinas ... bla, bla, bla ... »





Y todo el mundo pensaba: ¿es oscuro aquí, no puede ser un axioma de dicho complejo. No reconoce el truco, las matemáticas de 2 mil años tratando de deshacerse de este postulado y lo demuestran a través de otros postulados y axiomas. Al principio, los griegos y luego los árabes y luego los europeos. Y todo el mundo pensó que probó con éxito esta premisa, pero luego resultó que la prueba se basa en algunas obvias, pero no prueban la afirmación equivale a postular. Tales afirmaciones se habían acumulado enorme conjunto. Éstos son algunos de ellos:

1. Hay triángulos arbitrariamente grande
área 2. Hay triángulos semejantes
3. La suma de los ángulos de un triángulo es 180 °
4. El teorema de Pitágoras es verdaderos
5. La relación entre la circunferencia y el diámetro - constante e igual a pi
6. Dos líneas paralelas a una tercera son paralelas entre sí

El último punto, y juega un papel clave en la confusión de la geometría de Lobachevsky. Pero lo veremos más adelante.

Por último, los matemáticos más avanzados comenzaron a tratar de aplicar la prueba en contrario [Euclides] - es decir, se supone que el quinto postulado no es cierto, y deducir de ello ninguna contradicción. El primero fue un italiano Saccheri (primera mitad del siglo XVIII.), Lo cual es muy molesto que no podía encontrar una contradicción. Al final, que cometió un error en los cálculos, obtenemos una contradicción, y suspiró feliz.

Poco a poco, los matemáticos empezaron a sospechar algo. Y se hicieron intentos para abandonar el quinto postulado no es encontrar una contradicción, pero sólo para ver qué pasa. El primer éxito alcanzado Lambert, que en la segunda mitad del siglo XVIII. Él construyó una geometría coherente sobre la esfera, en la que la suma de los ángulos de un triángulo es siempre mayor que 180 ° y todas las líneas se intersectan. Sin embargo, en la geometría esférica se perturba no sólo el quinto postulado sino también al menos los tres primeros. Por cierto, la cuarta aún ha sido probado y se excluye de los postulados.

Lambert también estudió geometría en la que la suma de los ángulos de un triángulo es siempre inferior a 180 °, no encontró en conflicto, pero no podía imaginar tal pronuncian una esfera imaginaria. Por lo tanto, no profundizar en el tema, lo que limita la afirmación de que es imposible demostrar el quinto postulado.

Seguir trabajando en este Schweickart y Gauss. Gauss entiende perfectamente todo, pero sabía también lo que frotar tan venerable comunidad científica - nuestro propio riesgo. Zaminusili, entonces nada podrá publicar. Por lo tanto ambos son en sí tranquilo silencio en un tubo.

El primero que declaró públicamente la geometría no euclidiana era Lobachevsky. En primer lugar, en un informe en 1826, luego en 1829 en la publicación. Por supuesto llovió todos los baches, y casi perdió su cargo como rector de la Universidad de Kazan. Él fue malinterpretado y ridiculizado, tanto en Rusia como en el extranjero. Pero él siguió insistiendo y de pie, y se trasladó a un nuevo estudio de la geometría de la más lejana. Y desde entonces lleva su nombre.

Casi como en la canción se canta:
Uno merece el crédito, uno merece la
culpa Y Nikolai Ivanovich Lobachevsky es su nombre

Independientemente de Lobachevsky, pero tres años más tarde publica su trabajo en la geometría no euclidiana, matemático húngaro Bolyai, también sigue siendo desapercibido.

Gauss apreciaba el trabajo de Lobachevsky, pero sólo en la correspondencia privada. Incluso trató de aprender ruso para leer su publicación en idioma ruso. En 1860 (después de la muerte y Gauss, y Lobachevsky) correspondencia Gauss se hace pública y comentarios favorables sobre Lobachevsky llamar la atención sobre el científico ruso y sus ideas. En general, se ha hecho justicia, pero como siempre a título póstumo.

Así, en la geometría de Lobachevsky por el mismo punto se puede hacer por lo menos dos líneas rectas paralelas a esta, pero en general infinita. Parecería que una vez que las líneas paralelas pasan por un punto, se cruzan. Sí, se superponen, pero el truco es que no son paralelas entre sí, aunque los dos son paralelas a una tercera línea.

Y, además, como habrá adivinado, la suma de los ángulos de un triángulo es siempre menor que 180 °, el área del triángulo delimitado por una relación constante entre la circunferencia y el diámetro aumenta con el círculo, etc. Cosas como esas. Y el teorema de Pitágoras no está funcionando.

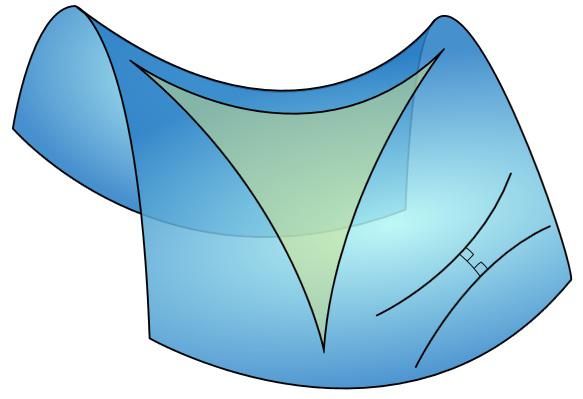
¿Cómo presentar una superficie en la que el trabajo de geometría Lobachevsky? Y aquí está - en KDPV, un triángulo con una muy sexy en su. Este llamado plano hiperbólico. Si la esfera - todas partes superficie convexa, el plano hiperbólico - cóncava todas partes, como una especie de embudo o una silla de montar, simplemente interminable. ¿Cómo es el radio de la esfera al (curvatura), y en el plano de Lobachevsky hay un cierto grado de curvatura. Sólo el alcance de esta curvatura es positiva, y en el plano Lobachevsky - negativo
.
En una escala muy pequeña, o mediante el aumento de la curvatura, la geometría euclidiana está cerca de Lobachevsky. Así, puede ser que vivimos en un espacio Lobachevsky con un bastante grande medida de curvatura, por lo que no se dan cuenta que en nuestra escala. En particular, la teoría de la relatividad se sigue que una distribución uniforme de la masa en el universo, nuestro espacio puede ser la geometría hiperbólica. De ser así, se le puede llamar matemáticas Lobachevsky Einstein.

Hoy se cumplen exactamente 221 años desde el nacimiento de Nikolai Ivanovich Lobachevsky. De lo que usted y felicitaciones!

PD A las líneas "paralelas" se cruzan en la geometría proyectiva, pero eso es otra historia.

Fuente: