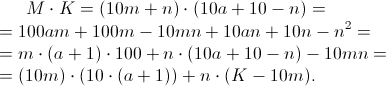1143
Ефективний рахунок в розумі або теплій для мозку
Ця стаття надихнула слоганом «Як і як швидко ти рахуєш у розумі на елементарному рівні?» і призначена для поширення техніки С.А. Рачинського для усного облікового запису.
Рахінський був видатним викладачем, який навчався в сільських школах XIX століття і показав свій досвід, що можна розвивати майстерність швидкого перорального підрахунку. Для своїх студентів не було особливо важко підрахувати такий приклад:
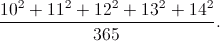
Використовуйте круглі номери.
Одним з найбільш поширених методів перорального підрахунку є те, що будь-який номер може бути представлений як сума або різниця чисел, один або більше з яких "круглий":
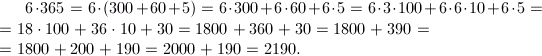
З 10, 100, 1000 і т.д., круглі номери переповнені швидше, розум повинен зменшити все до таких простих операцій, як 18 x 100 або 36 x 10. Відповідно, простіше додати, «сплітаючи» круглий номер, а потім додати «хвостик»: 1800 + 200 + 190.
Інший приклад:
Спрощуємо багатозастосування за поділом
У пероральному підрахунку зручніше використовувати дівидимий і дивізор, ніж ціле (наприклад, 5 представлена як 10:2, так і 50 представлена як 100:2):
Аналогічно, множити або розділити на 25, тому що 25 = 100:4. Наприклад,
Тепер не можна множити 625 за 53:
Кількість двох чисел
Вимкнено, що просто на площі будь-якого двоцифрового числа, досить пам'ятати квадрати всіх чисел від 1 до 25. На щастя, ми вже знаємо квадрати до 10 з багатозастосного столу. Решта квадратів можна побачити в таблиці нижче:

Рецепція Рачинського полягає в наступному. Для того, щоб знайти квадрат будь-якого двоцифрового числа, потрібно помножити різницю між цим числом і 25 по 100 і додати в отриманий продукт квадрат доповнення цього числа до 50 або площі його надлишок вище 50. Наприклад,
Загальний (M - двоцифровий номер):
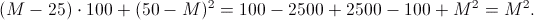
Ми спробуємо застосувати цей трюк при облаштуванні трицифрового числа, розділивши його заздалегідь в менші компоненти:
Ум, я б не сказав, що це набагато простіше, ніж покласти його в бар, але, можливо, ви можете налаштувати час.
І почати навчання, звичайно, слід з квадратом двох чисел, і вже можна розбиратися в розумі.
Застосування двох чисел
Ця цікава методика була винайдена 12-річному студенту Рахінського і є однією з варіантів додавання до круглого числа.
Дякуемо два дві цифри, сума яких 10:
Рахінський був видатним викладачем, який навчався в сільських школах XIX століття і показав свій досвід, що можна розвивати майстерність швидкого перорального підрахунку. Для своїх студентів не було особливо важко підрахувати такий приклад:
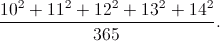
Використовуйте круглі номери.
Одним з найбільш поширених методів перорального підрахунку є те, що будь-який номер може бути представлений як сума або різниця чисел, один або більше з яких "круглий":
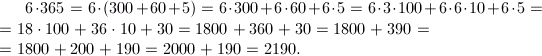
З 10, 100, 1000 і т.д., круглі номери переповнені швидше, розум повинен зменшити все до таких простих операцій, як 18 x 100 або 36 x 10. Відповідно, простіше додати, «сплітаючи» круглий номер, а потім додати «хвостик»: 1800 + 200 + 190.
Інший приклад:
31 х 29 = (30 + 1) х (30 - 1) = 30 х 30 - 1 х 1 = 900 - 1 = 899 Спрощуємо багатозастосування за поділом
У пероральному підрахунку зручніше використовувати дівидимий і дивізор, ніж ціле (наприклад, 5 представлена як 10:2, так і 50 представлена як 100:2):
68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400; 3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68 Аналогічно, множити або розділити на 25, тому що 25 = 100:4. Наприклад,
600 : 25 = (600 : 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600 Тепер не можна множити 625 за 53:
625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 25 = 33125 Кількість двох чисел
Вимкнено, що просто на площі будь-якого двоцифрового числа, досить пам'ятати квадрати всіх чисел від 1 до 25. На щастя, ми вже знаємо квадрати до 10 з багатозастосного столу. Решта квадратів можна побачити в таблиці нижче:

Рецепція Рачинського полягає в наступному. Для того, щоб знайти квадрат будь-якого двоцифрового числа, потрібно помножити різницю між цим числом і 25 по 100 і додати в отриманий продукт квадрат доповнення цього числа до 50 або площі його надлишок вище 50. Наприклад,
37^2 = 12 x 100 + 13^2 = 1200 + 169 = 1369; 84^2 = 59 x 100 + 34^2 = 5900 + 9 x 100 + 16^2 = 6800 + 256 = 7056; Загальний (M - двоцифровий номер):
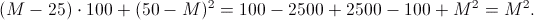
Ми спробуємо застосувати цей трюк при облаштуванні трицифрового числа, розділивши його заздалегідь в менші компоненти:
195^2 = (100 + 95)^2 = 10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 70 x 100 + 45^2 = 10000 + (90 +5) x 2 x 100 + 7000 + 5^2 = 17000 + 19000 + 2000 + 25 = 38025 Ум, я б не сказав, що це набагато простіше, ніж покласти його в бар, але, можливо, ви можете налаштувати час.
І почати навчання, звичайно, слід з квадратом двох чисел, і вже можна розбиратися в розумі.
Застосування двох чисел
Ця цікава методика була винайдена 12-річному студенту Рахінського і є однією з варіантів додавання до круглого числа.
Дякуемо два дві цифри, сума яких 10:
M = 10m + n, K = 10a + 10 - n.
При складанні своєї роботи ми отримуємо:
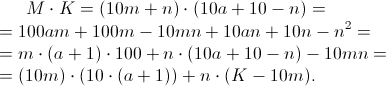
Наприклад, розрахувати 77 х 13. Сума юнітів цих чисел становить 10, тому що 7 + 3 = 10. По-перше, кладуть меншу кількість до збільшення: 77 x 13 = 13 x 77.
Для отримання круглих чисел ми приймаємо три одиниці з 13 і додаємо їх до 77. Тепер помножити нові номери 80 x 10, і до результату ми додаємо продукт вибраних 3 юнітів по різниці між старістю No 77 і новим числом 10:
13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001
Ця техніка має особливий випадок: все значно спрощено, коли два фактори мають однакову кількість десятків. У цьому випадку кількість десятків переповнена числом, що передається, і продукт одиниць цих чисел приписується до результату. Давайте подивимося, як елегантна ця техніка знаходиться в прикладі.
48 х 42. Кількість десятків 4, наступний номер: 5; 4 x 5 = 20.й Товар одиниць: 8 х 2 = 16 марй Так 48 x 42 = 2016.
99 х 91. Кількість десятків: 9, з 10; 9 x 10 = 90.00 Рй Товар одиниць: 9 х 1 = 09 марй Так 99 x 91 = 9009.
Так, щоб помножувати 95 x 95, просто підрахувати 9 x 10 = 90 і 5 x 5 = 25 і відповідь готова:
95 x 95 = 9025.
Потім попередній приклад можна розрахувати трохи простіше:
195^2 = (100 + 95)^2 = 10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 9025 = 10000 + (90 +5) x 2 x 100 + 9000 + 25 = 10000 + 19000 + 1000 + 8000 + 25 = 38025
Замість
Здавалося б, чому можна розраховувати на розум в 21 столітті, коли можна просто подарувати голосову команду смартфону? Але якщо ви думаєте про це, що буде людство, якщо це займе на машинах не тільки фізична робота, але і будь-яка психічна робота? Чи не він деградує? Навіть якщо ви не вважаєте словесним підрахунком в самому кінці, то цілком підходить для зміцнення розуму.
Література використана:
1001 р. Проблеми психічного обліку в школі С.А. Рачинського
Джерело: habrahabr.ru/post/207034/