1134
有效的费用在头脑中锻炼
这篇文章的灵感来自于一个话题«就像你想如何快速在你的心中,在小学阶段?»与技术设计上延续SA拉查口服帐户。
Raczynski是一个好老师,教农村学校在十九世纪,并指着自己的经验,开发出快速计数口语技能可能。对于他的弟子们并没有特别的问题找到心目中一个类似的例子:
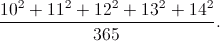
使用整数 H5>
按部门简化乘 H5>
现蕾两位数 H5>
两位数 H5>
的结论,而不是 H5>
Raczynski是一个好老师,教农村学校在十九世纪,并指着自己的经验,开发出快速计数口语技能可能。对于他的弟子们并没有特别的问题找到心目中一个类似的例子: