Gasto eficaz en el ejercicio de mente o el cerebro

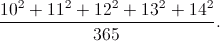
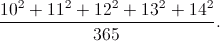
números redondos utilizando h5>
Uno de los métodos más comunes de la cuenta oral es que cualquier número puede representarse como una suma o diferencia de números, uno o más de ellos 'ronda »:



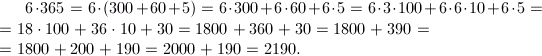
Desde en el 10 i>, 100 i>, 1000 i>, y otros. Redondea el número se multiplique rápidamente en la mente tiene que reducir todo a operaciones tan simples como 18 100 x i> o 36 x 10 i>. Por consiguiente, es más fácil de plegar, "escisión" número redondo, y después la adición de una "cola»: 1800+ 200+ 190 i>.
Otro ejemplo:

 & lt; code class = & quot; MATLAB & quot; & gt; 31 x 29 = (30 + 1) x (30-1) = 30 x 30-1 1 x = 900-1 = 899. & lt; / código de & gt; < / pre> 

simplificar la multiplicación por división h5>
Cuando la cuenta oral es más conveniente para operar en el dividendo y el divisor en lugar de un número entero (por ejemplo, 5 i> representa como 10: 2 i> y 50 i> a 100: 2 i>):

 & lt; code class = & quot; MATLAB & quot; & gt; = 68 x 50 (68 x 100): 2 = 6800: 2 = 3,400; 3400: 50 = (3400 x 2): 100 = 6800 = 100 68. & lt; / código de & gt;  pre> 

Del mismo modo, la multiplicación o división por  25  i>, porque  100 25 = 4  i>. Por ejemplo, 

 & lt; code class = & quot; MATLAB & quot; & gt; 600: 25 = (600: 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100): 4 = 2400 = 600. 4 & lt; / código de & gt;  pre> 

Ahora, parece imposible no multiplicarse en la mente  625  i> en  53  i>: 

 & lt; code class = & quot; MATLAB & quot; & gt; 625 x 53 = 625 x 50 ± 625 x 3 = (625 x 100): 2 + 600 x 3 + 25 x 3 = (625 x 100): 2 + 1800+ (20 + 5) x 3 = (60000 + 2500): 1800 + 60 + 15 2 + = 30000 + 1250 + 1800 + 50 + 25 = 33 000 50 50 25 = 33125. & lt; / código de & gt;  pre> 

cuadratura dígitos dobles h5>
Resulta simplemente construir cualquier número de dos dígitos en la plaza, que es suficiente para recordar los cuadrados de todos los números de la 1 i> a 25 i>. Afortunadamente, plazas hasta 10 i> que ya saben de las tablas de multiplicar. El resto de los cuadrados se puede ver en la siguiente tabla:



Admisión Racha es como sigue. Para encontrar el cuadrado de cualquier número de dos dígitos, usted tiene la diferencia entre este número y 25 i> veces el 100 i> para recibir el producto para añadir suplemento plaza este número a 50 i > exceso o cuadrar la vuelta 50 i> XX. Por ejemplo,

 & lt; code class = & quot; MATLAB & quot; & gt; 37 ^ 2 = 12 x 100 + 13 ^ 2 = 1200 + 169 = 1.369; 84 ^ 2 = 59 x 100 + 34 ^ 2 = 5,900 + 9 x 100 + 16 ^ 2 = 6800 + 256 = 7056; & Lt; / código de & gt;  pre> 

En general, el ( M  i> - número dos dígitos): 



 



Vamos a tratar de aplicar este truco cuando la cuadratura de un número de tres dígitos dividiéndola en pre-términos más pequeños: 

 & lt; code class = & quot; MATLAB & quot; & gt; 195 ^ 2 = (100 + 95) ^ 2 = 10,000 + 2 x 100 x 95 + 95 ^ 2 = 10.000 + 9.500 x 2 + 70 x 100 45 * 2 = 10 000 + (90 + 5) x 2 x 100 + 7000 + 100 + 20 x 5 ^ 2 = 17000 + 19000 + 2000 + 25 = 38025. & lt; / código de & gt;  pre> 

Hmm, yo no diría que es mucho más fácil que la erección de una columna, pero tal vez, con el tiempo, puede adaptarse. 

Y para comenzar el entrenamiento, por supuesto, ser un cuadrar números de dos dígitos, pero ya antes de desmontar la mente se puede llegar. 

La multiplicación de números de dos dígitos h5>
Esta técnica interesante fue inventado por 12 años, alumno de la Racha es una opción de añadir hasta un número redondo.
Considere los números de dos cifras cuya suma es igual a 10 unidades:

 & lt; code class = & quot; MATLAB & quot; & gt; H = 10 m + n, K = 10a + 10 - n. & Lt; / código de & gt;  pre> 

La composición de su trabajo, se obtiene: 



 



Por ejemplo, calculamos el  77 x 13  i>. La cantidad de unidades de estos números es  10  i>, como  7 + 3 = 10  i>. En primer lugar, poner menos antes del gran:  = 77 x 13 a 13 x 77  i>. 

Para obtener los números redondos, tomamos tres unidades de la  13  i>, y añadirlos a la  77  i>. Ahora multiplique los nuevos números de  80 x 10  i>, y el resultado añadir el producto seleccionado  3  i> unidades de la diferencia entre el número de edad  77  i> y los nuevos  10  i>: 

 & lt; code class = & quot; MATLAB & quot; & gt; 13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 800 + 7 = 180 + 21 + 201 = 800 = 1001. & lt; / código de & gt;  pre> 

Esta recepción es un caso especial: Es mucho más fácil cuando los dos factores el mismo número de decenas. En este caso el número se multiplica por las decenas seguido de un número, y se atribuye a los resultados de las unidades de trabajo de los números. Vamos a ver cómo elegante esta técnica con un ejemplo. 

 a 48 x 42  i>. Incluyendo docenas de  4  i>, número siguiente:  5  i>;  de 4 x 5 =  20   i>. Las unidades de trabajo:  un niño de 8 x 2 =  16   i>. Entonces, 

 & lt; code class = & quot; MATLAB & quot; & gt; 48 x 42 = 2016 & lt; / código de & gt;  pre> 

 99 x 91  i>. El número de decenas:  9  i>, número siguiente:  10  i>;  a 9 x 10 =  90   i>. Las unidades de trabajo:  a 9 x 1 =  09   i>. Entonces, 

 & lt; code class = & quot; MATLAB & quot; & gt; 99 x 91 = 9009. & lt; / código de & gt;  pre> 

Sí, hay que multiplicar el  95 x 95  i>, es suficiente para contar el  a 9 x 10 = 90  i> y  5 x 5 = 25,  i>, y la respuesta está listo: < br />

 & lt; code class = & quot; MATLAB & quot; & gt; 95 x 95 = 9025. & lt; / código de & gt;  pre> 

A continuación, el ejemplo anterior se puede calcular un poco más fácil: 

 & lt; code class = & quot; MATLAB & quot; & gt; 195 ^ 2 = (100 + 95) ^ 2 = 10,000 + 2 x 100 x 95 + 95 ^ 2 = 10.000 + 9.500 x 2 + 9.025 = 10.000 + (90 5) x 2 x 100+ 9000+ 25 = 19000 + 10000 + 8000 + 1000 + 25 = 38025. & lt; / código de & gt;  pre> 

En lugar de una conclusión h5>
Al parecer, ¿por qué debería ser capaz de contar en su mente en el siglo 21, cuando se puede presentar un smartphone comando de voz? Pero si usted piensa acerca de lo que va a pasar a la humanidad si se va a tomar en el coche, no sólo el trabajo físico, pero cualquier mental? No si se degrada? Incluso si usted no se considera una cuenta oral de un fin en sí mismo para el endurecimiento de la mente, que es muy adecuado.

Referencias «1.001 reto para la cuenta mental en la escuela SA Racha » i>.

Fuente: habrahabr.ru/post/207034/