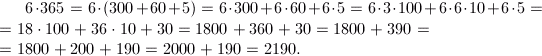Effective expense in the mind or brain workout

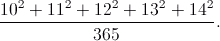
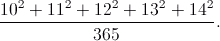
Using round numbers h5>
One of the most common methods of oral account is that any number can be represented as a sum or difference of numbers, one or more of them 'round »:



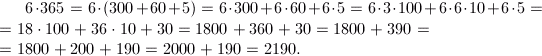
Since on the 10 i>, 100 i>, 1000 i>, and others. Round the number to multiply rapidly in the mind need to reduce everything to such simple operations such as 18 100 x i> or 36 x 10 i>. Accordingly, it is easier to fold, "splitting off" round number, and then adding a "tail»: 1800+ 200+ 190 i>.
Another example:

 & lt; code class = & quot; matlab & quot; & gt; 31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 1 x = 900 - 1 = 899. & lt; / code & gt; < / pre> 

simplify multiplication by division h5>
When oral account is more convenient to operate the dividend and divisor rather than an integer (for example, 5 i> represented as 10: 2 i>, and 50 i> a 100: 2 i>):

 & lt; code class = & quot; matlab & quot; & gt; = 68 x 50 (68 x 100): 2 = 6800: 2 = 3400; 3400: 50 = (3400 x 2): 100 = 6800 100 = 68. & lt; / code & gt;  pre> 

Similarly, the multiplication or division by  25  i>, because  100 25 = 4  i>. For example, 

 & lt; code class = & quot; matlab & quot; & gt; 600: 25 = (600: 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100): 4 = 2400 4 = 600. & lt; / code & gt;  pre> 

Now, it seems impossible not to multiply in the mind  625  i> on  53  i>: 

 & lt; code class = & quot; matlab & quot; & gt; 625 x 53 = 625 x 50 ± 625 x 3 = (625 x 100): 2+ to 600 x 3 + 25 x 3 = (625 x 100): 2+ 1800+ (20 + 5) x 3 = (60000 + 2500): 2+ 1800+ 60+ 15 = 30000 + 1250 + 1800 + 50 + 25 = 33,000 +50 +50 +25 = 33125. & lt; / code & gt;  pre> 

Squaring double digits h5>
It turns out to just build any two-digit number in the square, it is enough to remember the squares of all the numbers from the 1 i> to 25 i>. Fortunately, squares up to 10 i> we already know from the multiplication tables. The rest of the squares can be seen in the table below:



Admission Racha is as follows. To find the square of any two-digit number, you have the difference between this number and 25 i> times the 100 i> to receive the product to add square supplement this number to 50 i > excess or square it over 50 i> th. For example,

 & lt; code class = & quot; matlab & quot; & gt; 37 ^ 2 = 12 x 100 + 13 ^ 2 = 1200 + 169 = 1369; 84 ^ 2 = 59 x 100 + 34 ^ 2 = 5900 + 9 x 100 + 16 ^ 2 = 6800 + 256 = 7056; & lt; / code & gt;  pre> 

In general, the ( M  i> - two-digit number): 



 



Let's try to apply this trick when squaring a three-digit number by breaking it into smaller pre-terms: 

 & lt; code class = & quot; matlab & quot; & gt; 195 ^ 2 = (100 + 95) ^ 2 = 10000 + 2 x 100 x 95 + 95 ^ 2 = 10000 + 9500 x 2 + 70 x 100 +45 * 2 = 10000 + (90 + 5) x 2 x 100 + 7000 + 100 + 20 x 5 ^ 2 = 17000 + 19000 + 2000 + 25 = 38025. & lt; / code & gt;  pre> 

Hmm, I would not say that it is much easier than the erection of a column, but maybe, with time, you can adapt himself. 

And to begin training, of course, be a squaring two-digit numbers, but already there before disassembling the mind can be reached. 

The multiplication of two-digit numbers h5>
This interesting technique was invented by 12-year-old pupil of the Racha is an option to add up to a round number.
Consider two-digit numbers whose sum is equal to 10 units:

 & lt; code class = & quot; matlab & quot; & gt; M = 10m + n, K = 10a + 10 - n. & lt; / code & gt;  pre> 

The composition of their work, we get: 



 



For example, we calculate the  77 x 13  i>. The amount of units of these numbers is  10  i>, as  7 + 3 = 10  i>. First, put fewer before the big:  = 77 x 13 to 13 x 77  i>. 

To get round numbers, we take three units of the  13  i>, and add them to the  77  i>. Now multiply the new numbers  80 x 10  i>, and to the result add the product selected  3  i> units in the difference between the old number  77  i> and the new numbers  10  i>: 

 & lt; code class = & quot; matlab & quot; & gt; to 13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 + 201 = 800 = 1001. & lt; / code & gt;  pre> 

This reception is a special case: It's much easier when the two factors the same number of tens. In this case the number is multiplied by the tens followed by a number, and is attributed to the result of the work units of the numbers. Let's see how elegant this technique with an example. 

 to 48 x 42  i>. Including dozens of  4  i>, following number:  5  i>;  of 4 x 5 =  20   i>. Work units:  an 8 x 2 =  16   i>. Then, 

 & lt; code class = & quot; matlab & quot; & gt; to 48 x 42 = 2016. & lt; / code & gt;  pre> 

 99 x 91  i>. The number of tens:  9  i>, following number:  10  i>;  a 9 x 10 =  90   i>. Work units:  a 9 x 1 =  09   i>. Then, 

 & lt; code class = & quot; matlab & quot; & gt; 99 x 91 = 9009. & lt; / code & gt;  pre> 

Yeah, you have to multiply the  95 x 95  i>, is sufficient to count the  a 9 x 10 = 90  i> and  5 x 5 = 25,  i>, and the answer is ready: < br />

 & lt; code class = & quot; matlab & quot; & gt; 95 x 95 = 9025. & lt; / code & gt;  pre> 

Then, the previous example can be calculated a little easier: 

 & lt; code class = & quot; matlab & quot; & gt; 195 ^ 2 = (100 + 95) ^ 2 = 10000 + 2 x 100 x 95 + 95 ^ 2 = 10000 + 9500 x 2 + 9025 = 10000 + (90 +5) x 2 x 100+ 9000+ 25 = 19000 + 10000 + 8000 + 1000 + 25 = 38025. & lt; / code & gt;  pre> 

Instead of a conclusion h5>
It would seem, why should be able to count in your mind in the 21st century, when you can just submit a voice command smartphone? But if you think about what will happen to humanity if it is to take on the car, not only the physical work, but any mental? Not whether it degrades? Even if you do not consider an oral account of an end in itself for hardening of the mind, he is well suited.

References «1001 challenge for mental account in the SA school Racha » i>.

Source: habrahabr.ru/post/207034/