教我儿子在一分钟内 找到多边形的区域

如何找到支票上描绘的多边形区域? 在20秒内可以做到吗? 没有坐标、精确度和复杂的计算 而解决考试上的问题,例如计算瓦片地板面积,将有利于奥地利数学家格奥尔格·皮克的公式.

(英语).

在学校里,我们被告知一个复杂的数字应该适合一个矩形. 然后找到所有附加数字的区域,矩形本身的区域并从中减去附加区域的数量.

(英语).

例如,三角形ABC的区域S可以通过从矩形区域S1,S2和S3的区域中减去来计算出. 但如果多边形是复杂的,还有许多额外的数字,那么这种方法就变得相当乏味了.

(中文(简体) ).

为了简化任务,并且没有公式,可以计算出所有的单元格. 然而,其中一些只是数字的一半。 在我们的三十六个细胞的三角形中,完整的有十五个,不完整的有二十一个. 有条件的,可以将2个不完全的细胞视为1个完整. 然后三角形的面积会为15+21/2=25.5个细胞.

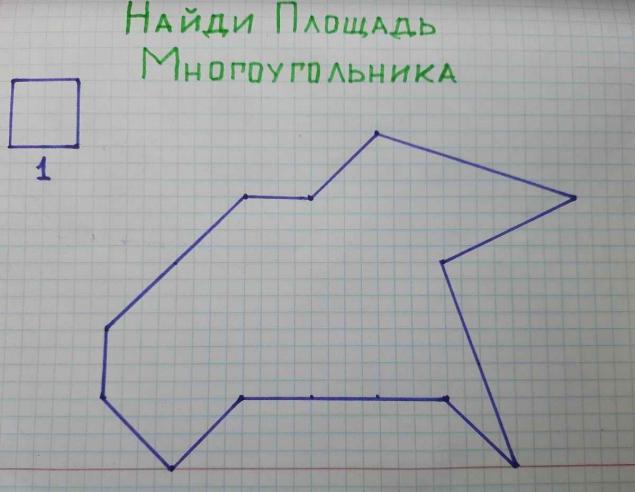(英语).

但是,这是一个粗略的估计。 比较容易和准确的计算。 峰顶定理老师不会告诉每个人。 听起来是这样: 网格节点有顶点的多边形区域可以通过公式找到
S = N - 1 + M/2

N 是多边形内的节点数
M 是多边形边界上的线条节点数

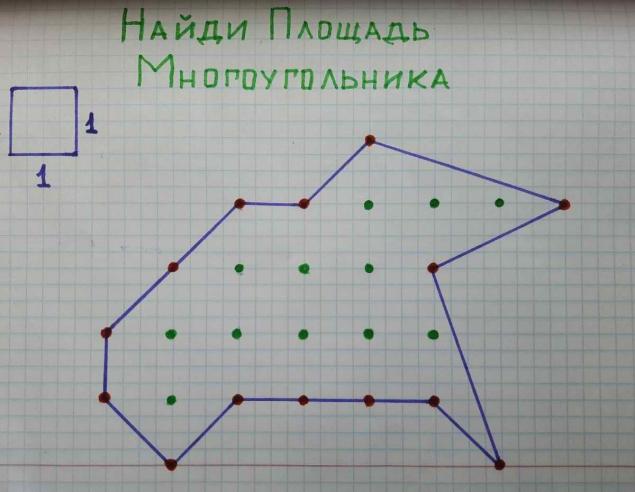(中文(简体) ).

就我们的情况来说,为了明确起见,我们采取一个方形,在4个细胞内有侧面作为网格细胞. 然后在图12的结晶(绿色点)和多边形14个结晶(红色点)的边界上. N = 12个,M = 14. 替换 公式: S=12-1+14/2=18

(英语).

为了巩固技能,尝试计算出另一个数字的区域,并在评论中分享结果,同时以传统方式重新检查. 显然,付出的努力和所花的时间是无法弥补的。

(英语).

注意:峰平方只为多边形工作,其顶点位于坐标网格的节点. 不幸的是,完全取代计算该地区的通常公式不会奏效,所以无论如何你都不应该忘记这些公式。 如你所见,数学可以很有趣。 为了吸引年轻学生, 将帮助挑选出七本迷人的书籍, 我们提供给读者。