Навчіть сина, щоб знайти область полігону в хвилину без проекту Bashny.Net

Як знайти область полігону зображено на зареєстрованому папері? І можна це зробити за 20 секунд без координат, тангенсів і складних розрахунків? І розв'язуючи проблеми на іспиті, і, наприклад, розрахунок площі плиткового поверху полегшить формулу австрійського математика Георга Пікака.



У школі ми навчили, що складна фігура повинна входити в прямокутник. Потім знайдіть площу всіх додаткових фігур, область прямокутника і відніміть кількість додаткових зон від неї.



Наприклад, площа S трикутника ABC може бути обчислена шляхом відрахування від площі прямокутних площ S1, S2 і S3. Але якщо полігон є складним, і є багато додаткових фігур, то цей метод стає досить нудним.



Щоб спростити завдання і зробити без формул, можна розраховувати всі клітинки. Однак деякі з них лише половина всередині фігури. У нашому трикутнику 36 клітин, повні - 15 і неповні - 21. Станом на 2 неповних клітин можна приймати як 1 комплект. Потім область трикутника буде 15 + 21/2 = 25.5 клітин.



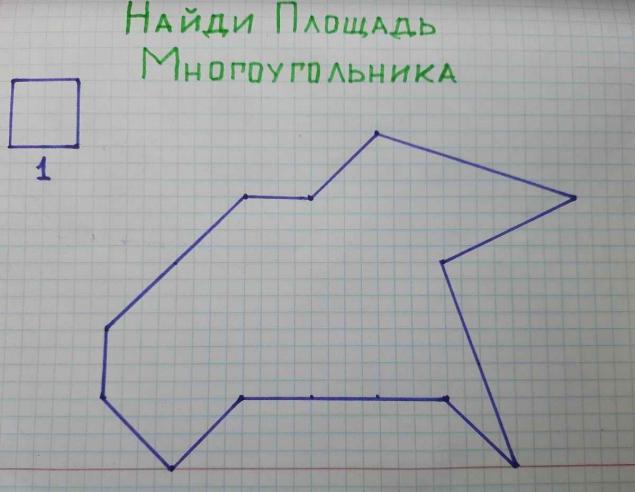
Але це груба оцінка. Простіше і більш точне для розрахунку. теорема ПікакаУ школі викладачі не розповідають всіх. Вона звучить так: область полігону з вершинами в вузлах сітки можна знайти за формулою
С = Н - 1 + М /

N - кількість вузлів в полігоні
M - кількість вершин решітки на полігонному кордоні



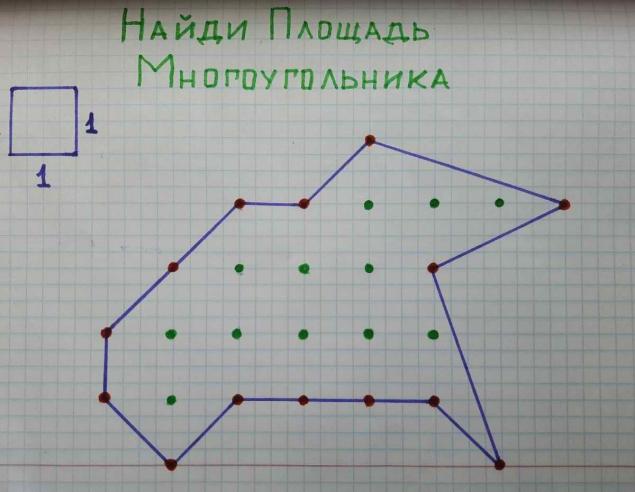
У нашому випадку для чіткості ми беремо квадрат з боками в 4 клітинах як сітчастий елемент. Далі всередині фігури 12 вузли решітки (зелені точки), а на межі полігону 14 вузлів (червоні точки). Н = 12 і М = 14. Напис формула: S = 12 - 1 + 14/2 = 18



Щоб закріпити майстерність, спробуйте підрахувати площу іншої фігури і поділитися результатом в коментарях, а в той же час перегляньте її традиційним способом. Очевидно, що зусилля і час, що закінчується, є некомерційними.



Зверніть увагу, що формула Peak працює тільки для полігонів, вершини яких розташовані в вузлах координатної сітки. Повністю замініть звичайні формули для розрахунку площі, на жаль, не вийде, тому не варто забувати їх в будь-якому випадку. Як ви бачите, математика може бути цікавою. І залучити юних студентів допоможе вибір 7 захоплюючих книг, які ми пропонуємо нашим читачам.