168
2021-06-25
Научил сына находить площадь многоугольника за минуту без черновика
Как найти площадь многоугольника, изображенного на клетчатой бумаге? И можно ли сделать это за 20 секунд без координат, тангенсов и сложных вычислений? И решение задач на ЕГЭ, и, например, вычисление площади плиточного пола облегчит формула австрийского математика Георга Пика.


Например, площадь S треугольника АВС можно вычислить вычитанием из площади прямоугольника площадей S1, S2 и S3. Но если многоугольник сложный, а дополнительных фигур много, то такой способ становится довольно утомительным.

Упростить задачу и обойтись без формул можно, посчитав все клеточки. Однако некоторые из них только наполовину находятся внутри фигуры. В нашем треугольнике из 36 клеточек полных — 15, а неполных — 21. Условно 2 неполных клетки можно принять за 1 полную. Тогда площадь треугольника будет равна 15 + 21/2 = 25,5 клеток.
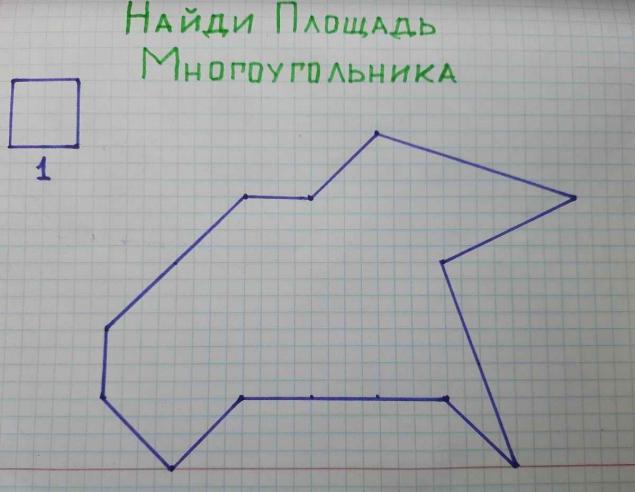
Но это приблизительный подсчет. Посчитать проще и точнее позволяет теорема Пика, о которой в школе, к сожалению, учителя рассказывают далеко не всем. Звучит она так: площадь многоугольника с вершинами в узлах сетки может быть найдена по формуле
S = N – 1 + M/2
N — количество узлов решетки внутри многоугольника
M — количество узлов решетки на границе многоугольника
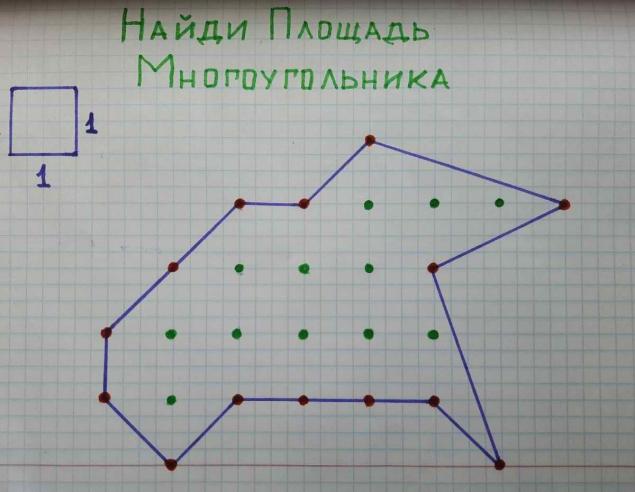
В нашем случае для наглядности за ячейку решетки мы принимаем квадрат со сторонами в 4 клетки. Тогда внутри фигуры 12 узлов решетки (зеленые точки), а на границе многоугольника 14 узлов (красные точки). N = 12, а M = 14. Подставляем в формулу: S = 12 – 1 + 14/2 = 18

Для закрепления навыка попробуй подсчитать площадь еще одной фигуры и поделись результатом в комментариях, а заодно перепроверь его традиционным способом. Очевидно, что затраченные усилия и время несоизмеримы.

Учти, что формула Пика работает лишь для многоугольников, вершины которых находятся в узлах координатной сетки. Полностью заменить ею обычные формулы вычисления площади, к сожалению, не получится, поэтому забывать их ни в коем случае не стоит. Как видишь, и математика может быть интересной. А увлечь ею маленьких учеников поможет подборка из 7 увлекательных книг, которую мы предлагаем вниманию наших читателей.

Как найти площадь многоугольника
В школе нас учили, что сложную фигуру нужно вписать в прямоугольник. Затем найти площадь всех получившихся дополнительных фигур, площадь самого прямоугольника и вычесть из нее сумму дополнительных площадей.
Например, площадь S треугольника АВС можно вычислить вычитанием из площади прямоугольника площадей S1, S2 и S3. Но если многоугольник сложный, а дополнительных фигур много, то такой способ становится довольно утомительным.

Упростить задачу и обойтись без формул можно, посчитав все клеточки. Однако некоторые из них только наполовину находятся внутри фигуры. В нашем треугольнике из 36 клеточек полных — 15, а неполных — 21. Условно 2 неполных клетки можно принять за 1 полную. Тогда площадь треугольника будет равна 15 + 21/2 = 25,5 клеток.

Но это приблизительный подсчет. Посчитать проще и точнее позволяет теорема Пика, о которой в школе, к сожалению, учителя рассказывают далеко не всем. Звучит она так: площадь многоугольника с вершинами в узлах сетки может быть найдена по формуле
S = N – 1 + M/2
N — количество узлов решетки внутри многоугольника
M — количество узлов решетки на границе многоугольника

В нашем случае для наглядности за ячейку решетки мы принимаем квадрат со сторонами в 4 клетки. Тогда внутри фигуры 12 узлов решетки (зеленые точки), а на границе многоугольника 14 узлов (красные точки). N = 12, а M = 14. Подставляем в формулу: S = 12 – 1 + 14/2 = 18

Для закрепления навыка попробуй подсчитать площадь еще одной фигуры и поделись результатом в комментариях, а заодно перепроверь его традиционным способом. Очевидно, что затраченные усилия и время несоизмеримы.

Учти, что формула Пика работает лишь для многоугольников, вершины которых находятся в узлах координатной сетки. Полностью заменить ею обычные формулы вычисления площади, к сожалению, не получится, поэтому забывать их ни в коем случае не стоит. Как видишь, и математика может быть интересной. А увлечь ею маленьких учеников поможет подборка из 7 увлекательных книг, которую мы предлагаем вниманию наших читателей.
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.
Рыбак из Мурманска умоляет не делать постыдных ошибок в засолке красной рыбы
Добавляют ли испанские хозяйки клубнику в гаспачо и стоит ли так делать





































