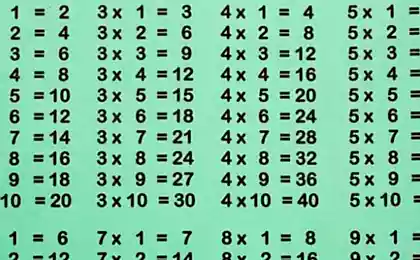549
Учитель математики розповів, як швидко дізнатися багатозастосунок і без нервів
Як освоїти багатозастосувальний стіл без прийняття багато часу від дітей? Сайт публікує чудовий метод від вчителя школи Катерина Кукіна. Ви, мабуть, чули, що рівень математики опадають.
Я зрозумів, Чому виникає рівень математики в школі? Це в другому класі, при укладанні фундаменту математичної освіти, що виникає таке гігантське незамінне отвір.
Основна проблема в багатостоянковому столі. Дивитися на клітку ноутбуків учні.
Я пройшов покупки для ноутбуків протягом тривалого часу. І все ж, у нас є така картина:
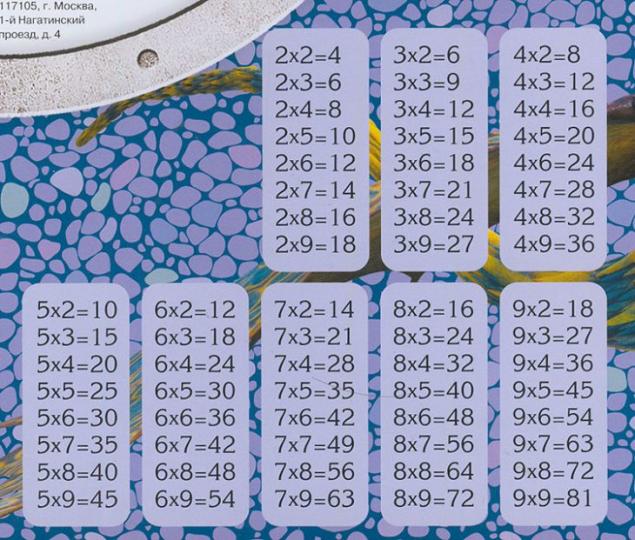
Джерело: Kukina-kat.livejournal.com Є ще гірше ноутбуків (для старших школярів), які не мають багатозастосувальних таблиць, але є купа безглуздих формул.
Так що це неправильно з цим ноутбуком? Невибагливий батько бачить багатозастосувальний стіл на блокнот. Здається, що все життя на блокнотах було багатозастосним столиком. Що неправильно?
Проблема полягає в тому, що ноутбук не має багатозастосувань таблиці.
Множення таблиці, мої шановні читачі, це:
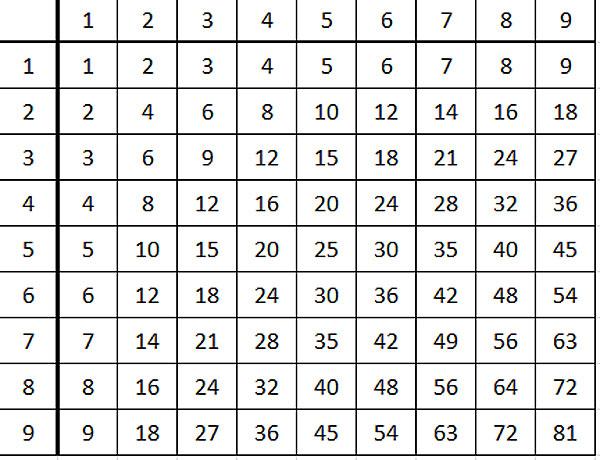 р.
р.
Це також називається Pythagoras Table.
Верхні і ліві стовпчики не можна брати, тільки основний прямокутник.
Спочатку це стіл. По-друге, Цікаво!
Немає дитини буде виглядати на прикладах, написаних у стовпчиках.
Не дитина може знайти цікаві риси і візерунки в письмових прикладах.
І в цілому, коли учитель каже: «Learn the multiplication Table», і дитина навіть не бачить столи перед ним, він відразу розуміє, що математика є наукою, де звичайні речі називаються по-різному, і вам потрібно дізнатися багато, багато, і зрозуміти нічого неможливо.
Який кращий стіл?
Крім того, дитина автоматично шукає візерунки. І він знаходить себе. Такі візерунки виявляються навіть дітьми, які ще не знають, як розмножуватися.
Наприклад, числа, які симетрично по відношенню до діагоналі рівні.
Людина-музей просто налаштовується, щоб подивитися на симетрію, і якщо вона знаходить її і помітить її, вона дуже щаслива. Що означає? Це означає, що з перевороту місць чинників, продукт не змінюється.
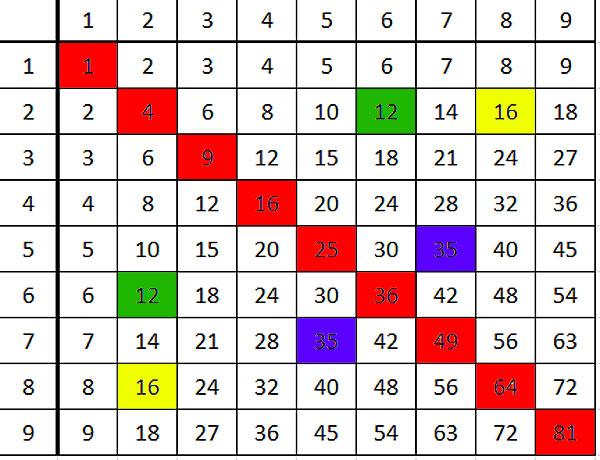
Ви бачите, дитина помітить себе! І який чоловік придумав себе, він назавжди запам'ятається, на відміну від того, що він запам'ятався або був сказав.
Веб-камера
Я зрозумів, Чому виникає рівень математики в школі? Це в другому класі, при укладанні фундаменту математичної освіти, що виникає таке гігантське незамінне отвір.
Основна проблема в багатостоянковому столі. Дивитися на клітку ноутбуків учні.
Я пройшов покупки для ноутбуків протягом тривалого часу. І все ж, у нас є така картина:

Джерело: Kukina-kat.livejournal.com Є ще гірше ноутбуків (для старших школярів), які не мають багатозастосувальних таблиць, але є купа безглуздих формул.
Так що це неправильно з цим ноутбуком? Невибагливий батько бачить багатозастосувальний стіл на блокнот. Здається, що все життя на блокнотах було багатозастосним столиком. Що неправильно?
Проблема полягає в тому, що ноутбук не має багатозастосувань таблиці.
Множення таблиці, мої шановні читачі, це:
 р.
р.Це також називається Pythagoras Table.
Верхні і ліві стовпчики не можна брати, тільки основний прямокутник.
Спочатку це стіл. По-друге, Цікаво!
Немає дитини буде виглядати на прикладах, написаних у стовпчиках.
Не дитина може знайти цікаві риси і візерунки в письмових прикладах.
І в цілому, коли учитель каже: «Learn the multiplication Table», і дитина навіть не бачить столи перед ним, він відразу розуміє, що математика є наукою, де звичайні речі називаються по-різному, і вам потрібно дізнатися багато, багато, і зрозуміти нічого неможливо.
Який кращий стіл?
- По-перше, немає сміття і шуму інформації у вигляді лівого боку прикладів.
- По-друге, ви можете подумати про це. Не скажеш ніде, що це багатозастосування є лише столиком.
- По-третє, якщо це постійно під рукою, і дитина постійно торкається на ній, він буде-ніль починає пам'ятати ці цифри. Зокрема, він ніколи не відповідав «55» на запитання «сім вісім», адже 55 не в таблиці взагалі.
Крім того, дитина автоматично шукає візерунки. І він знаходить себе. Такі візерунки виявляються навіть дітьми, які ще не знають, як розмножуватися.
Наприклад, числа, які симетрично по відношенню до діагоналі рівні.
Людина-музей просто налаштовується, щоб подивитися на симетрію, і якщо вона знаходить її і помітить її, вона дуже щаслива. Що означає? Це означає, що з перевороту місць чинників, продукт не змінюється.

Ви бачите, дитина помітить себе! І який чоловік придумав себе, він назавжди запам'ятається, на відміну від того, що він запам'ятався або був сказав.
Веб-камера
Як помер Сергій Бодров: таємничі факти про трагедії в кармадонському горзі
Найпопулярніші відео: 20 фіналістів!