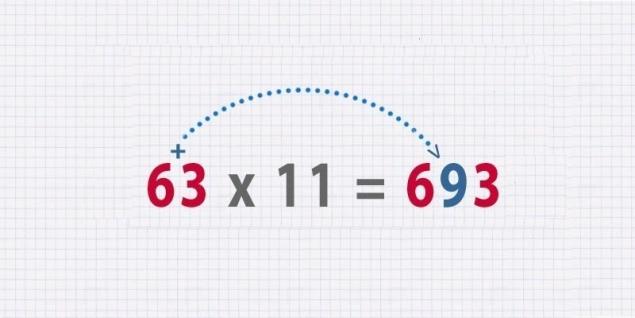Як навчити дитину словесним підрахунком

Я розмовляв мій друг на телефоні, і вона в міжмові мене, як важко її дочка дається багатозастосунковий стіл: «Ви не можете пояснити логічно, вам потрібно запам’ятати, і для нас це реальна проблема, навіть якщо ви лікуєте. й





Здавалося б, тільки диво може врятувати батьків від сліз над блокнотами молодих студентів. На щастя, в житті Гаррі Поттера не менше див.





Завдяки математичним секретам і хитрощам з "Сайт" Ваша дитина зможе любити королеву наук, і розмножувати і розділити на розумі буде легше!

Оральні прийоми рахунків

1. Миттєве багатокористування від 11
   Багато в чому Якщо ви знаєте секрет. Розглянемо наступний приклад: 63 x 11.
   Щоб вирішити це, потрібно лише додати цифри, які складають перший номер (6 + 3 = 9), а потім розмістити дев'ять між шістьм і трьома. Ось наше рішення: 693.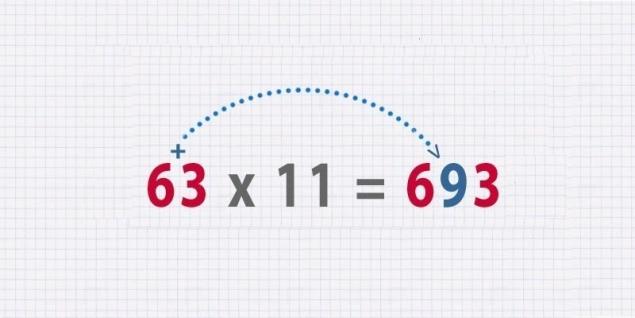
   
   
   
   Якщо сума цифр є двома цифрами, то алгоритм змінюється трохи. Скажіть приклад 86 x 11. Хоча 8 + 6 = 14, відповідь не 8146. Як і раніше, число 4 поміщається між номерами 8 і 6, але 1 додається в число 8, щоб отримати правильну відповідь 946.
   
   
   
   
   
   «Якщо дитина не розуміє найпростіших математичних концепцій, то це не означає, що він приступив.» Ми просто не зустрілися з досить чітким поясненням! Вивчіть правила багатозастосувань без особливих труднощів, дитина допоможе столику Pythagoras. Більше інформації. Просто цифри і логічне мислення.
   
   
2. Багатозастосування чисел, що складаються з блоків самостійно
   Взяти цей столик в сервіс, буде легше вирішувати такі приклади з ним.
   
   
   
3. Простий спосіб розмноження на 9
   Для розмноження будь-якого числа від 1 до 9 по 9, подивіться на руки. Повернути пальцем, який відповідає багатопліфікованому номеру (наприклад, 9×6 – гниття шостого пальця), підрахуйте пальцями до гнутого пальця, він буде десятками (в разі 9×6 є 5), потім підрахуйте пальці після згину, це буде одиниці (в нашому випадку є 4). Відповідь 54.
   
   
   
   Щоб краще пам'ятати багатозастосунок, цей смішний візерунок буде приходити в зручний. Як ви помітили, цифри в першому стовпчику збільшують кожен раз, а в другому стовпчику знижують 1.
   
   
   
   
   
   Привіт, що математика є дуже цікавим предметом, і свого роду гри, головоломки. Ми пропонуємо нашим читачам.
   
   
4. Багаторазове використання трьох чисел за окремими цифрами
   Все, що ви повинні зробити, це зламати велику проблему в кілька маленьких. Наприклад: 340 x 7. Перерва 340 в 300 і 40. Мульті 300 від 7 і 40 до 7 індивідуально, і додайте отримані числа: 2100 + 280 = 2380.
5. Кількість двох чисел
   Якщо кількість, яка повинна бути квадратною, близько до кількості, площа якого легко розпізнати, то можна скористатися наступним способом: додати число себе до площі числа за одиницю менше і кількість за одиницю менше. Наприклад: 31^2 = 30^2 + 31 + 30 = 961.
6. Кількість номерів, що закінчуються в 5
   Ця техніка допоможе швидко площі двоцифрового числа, який закінчується 5. Все, що ви повинні зробити, це множити перший номер номер, який ще один і покласти 25 в кінці.
   
   
   
   Наприклад: 85 кв.м. Крок 1. Помножити першу цифру на першому цифрі, збільшеному на одному: 8 (8 + 1) = 72. Крок 2. До 25: виходить 7225.
   
   
7. Розділ 5
   Розділення великих чисел на 5 дуже просто. Вам просто потрібно помножити кількість на 2 і перемістити кому. Наприклад: 235/5. Multiply 235 від 2 (235 x 2 = 470). Трансфер коми зліва: 47.0 або всього 47.
8. Комплексне багатозастосування
   Ви хочете знати, Як багатошарові великі цифри у вашому розумі? Якщо один з них навіть, ви можете просто перегрупувати номери, щоб полегшити відповідь:
   32 х 125 = 16 х 250 = 8 х 500 = 4 х 1000 = 4000.
   
   
   
9. Простий метод пошуку відсотка будь-якого числа
   Щоб знайти простий відсоток номеру (наприклад, 40% від 600), поділіть цифри на 10 і помножте результати між ними (4 х 60 = 240).
10. Чарівна кількість 1,089
    Візьміть будь-який трицифровий номер, цифри якого в порядку зменшення (наприклад, 932 або 876). Тепер напишіть його в зворотному порядку і відніміть його з початкового числа. Додати результат відступу, письмового зворотного замовлення. Візьміть номер 932: 932 - 239 = 693. До результату ми додаємо його в зворотному порядку і отримуємо магічний номер 1089: 693 + 396 = 1089.
    
    Або номер 876: 876 - 678 = 198. До результату ми додаємо запис у зворотному порядку і отримуємо той же номер 1089: 198 + 891 = 1089.
    
    

Великий італійський фізик, філософ і астроном Galileo Galilei колись сказав: «Математика – мова, в якій написано книгу природи». Ми сподіваємося, що завдяки нашим прикладам, навчання для вашої дитини буде цікавим і цікавим!