1489
Так вважається древньою. Український
Про історію обчислень і підрахунку. Перша стаття про Єгипет тут.
Тепер я збираюся поговорити трохи про ще одну велику цивілізацію і культуру минулого. Вавилонський царства виник на початку 2-го тисячоліття до н.е., він замінив Sumer і Akkad і існував перед завоюванням персид у 539 р. до н.е. Написав в Вавилон, так як всі пам'ятають, на глиняних таблетках з туніформою, які дуже добре збережені на відміну від паперу, папірусу і аналогічних речей, тому ми знаємо досить багато про Вавилон, а про її математику. Ми не знаємо все. На відміну від греків, валоняни не залишають чітких алгоритмів або чітких пояснень їх техніки. Тепер ми можемо тільки вгадати, як саме вавилонський, діяв в цьому або тому випадку в вирішенні проблеми. У цій роботі я концентрую переважно на вавилонський арифметметику, залишивши при цьому геометрію, алгебра, астрономію.
Вавилонський просунувся набагато далі в математики, ніж єгиптяни, наскільки ми знаємо, хоча вони не збіглися з греками. Вони вже знали, як розв’язати квадарні рівняння, а також мали ряд об’єктів чисельної алгебри. Однією з їх досягнень стала запровадження позиційної шестивимірної системи номеру без нуля. Це означає, що обробка чисел стала набагато більш гнучкою і простою, ніж в Єгипті. Невідомо, що ця система з'явилася. Один варіант говорить про те, що він привів до змішування 6- і 10-річних систем людей Сумера і Akkad. Але є інші думки про це.
На жаль, ця система (і, можливо, не хотів би навчити їх багатозастосунковий стіл) не освоїлася іншими людьми Стародавнього світу, і ми повинні чекати прибуття індійської системи. Однак деякі відбиття вавилонської математики залишаються в нашій культурі: поділ хвилини на шістдесяти секунд і година в 60 хвилин є ехо давньої вавилонської системи.
Кількість номерів та номерна система
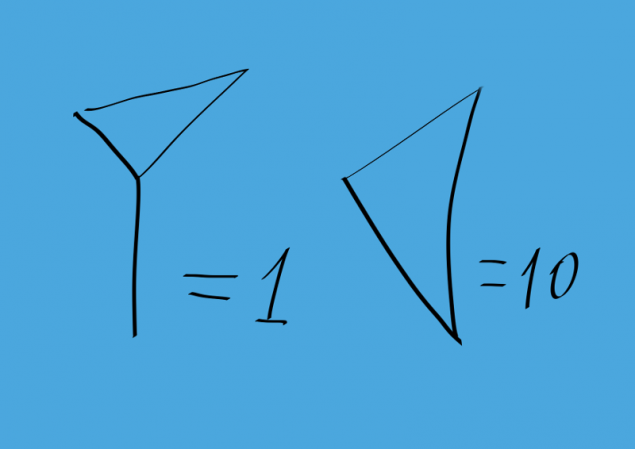
На малюнку показано, як валоняни позначені 1 і 10. Всі номери від 1 до 59 представлені. На малюнку нижче показано номер 33. Це схоже на римські та інші непозиційні системи написання номеру.
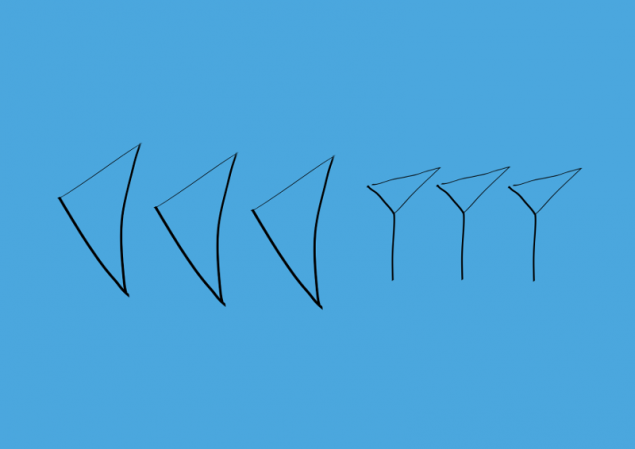 р.
р.
Кількість 60 точно так само, як і один. На початку було намальовано більше, але пізніше ця відмінність була вилучена. Кількість номерів понад 60, але не менше 120, ніж 120, були занепадані наступним чином: спочатку було написано номер 60, потім решта кількості менше 60 було написано через простір.
Нижче наведено приклад No 63.

Кількість форм K*60+n (1<=K<60; n=1, 2, 3, ... 59) були позначені аналогією, як в прикладі нижче.
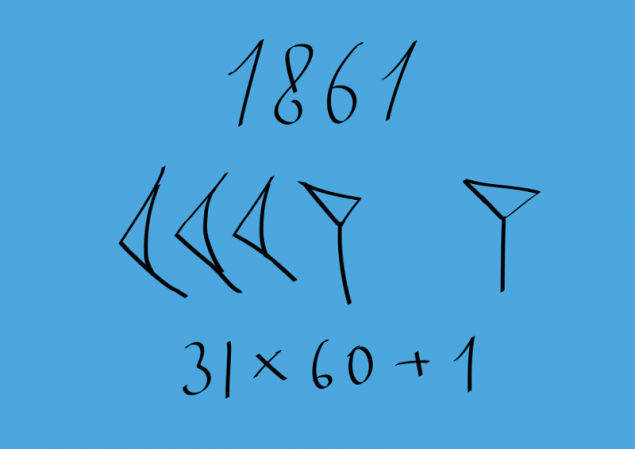
Вавилонський не мав 0, але з часом вони приходили до знака, що заперечували пропущені ряди. Ця ознака була використана тільки для укусів в межах числа і не була поставлена в кінці. Ось приклад на малюнку.
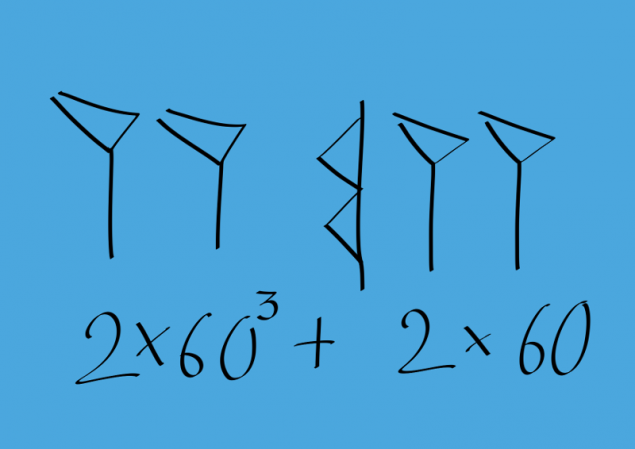
Проблема в тому, що цей номер може бути прочитаний як 2 * 60^2 +2, так і 2 * 60^5 +2 * 60^3. Дуже зручно! Ця система запису повинна призвести до численних помилок, які ви не думаєте? Вавилонський намагався дуже ретельно відокремити ряди, щоб уникнути сплутаності (міше ніж я зробив). У деяких випадках помилки дуже ймовірні. Приклади великих чисел відомі, коли частина номеру передається на іншу лінію. Спробуйте дізнатися, що ви означали! Але кількість помилок у валонських текстах невелика, хоча вони закінчуються.
Таким чином, вони також визначаються дроби. Тільки для дуже популярних 1/2, 1/3 і 2/3 були спеціальні іконки.
Девер я ходжу, я написаю валонські числа, розділяючи кому і всю частину від фракційного з півколоном. Наприклад: 177 є 2.57 і т.д. Змішані цифри, я замінив 0.
Розрахунок
Так як валонська система була позиціональною, їх розрахунки були схожими на нашу. При скороченні та додаванні вони просто додаються і відхилені числа трохи. Додаткова перевага була в тому, що шість цифр були денотовані в непозиційному вигляді за допомогою юнітів і десятків, і в такій системі набагато простіше відслідковувати і додати, ніж в наших абстрактних позначеннях, які вимагають вивчення особливої таблиці доповнення.
Багатокористування, як ви можете здогадатися, був схожий на наш. Але як вони використовують свій величезний багатозастосувальний стіл? Вивчивши це серцем? Вони приготували спеціальні столи, де вони могли дивитися роботи.
Багатофункціональні столи зійшли до нас з Вавилонян, але вони не включають в себе всі твори «єдиних» чисел, таких як наші десяткові столи. З 1 по 20 інклюзивних таблиць, з якими працює 30, 40, 50. Якщо вавилонський бажав розмножуватися 35 від 47, то йому довелося знайти в таблиці спочатку 35*40, а потім 35*7 і додати. Це вимагає додаткових дій, але таким чином можна було зберегти багато місця.
Вавилони не знали поділу як самостійна дія. замість цього вони використовували багатозастосування за зворотним номером. Для цього, звичайно, вони потрібні таблиці задніх чисел. Наприклад, якщо вам довелося розділити 1.15 на 5, Бабилонський знайдеться 1/5, що в їх записі буде 0;12 і множать 1.15 по 0;12. Якщо такий номер не був виражений скінченною шістдесятикратною дробою, то вавилоняни шукали номер, який, коли множили дивізором, дав дівидимість.
Наприклад, розділіть 22.45.0 на 6.30. Що потрібно взяти з 6.30, щоб отримати 22.45.0? Відповідь 3.30. Звісно, вавилоняни використовували приблизні значення при необхідності.
Неперевершені таблиці виглядають як це:
2 30 3 20 4 15 6 10 8 7;30 9 6;40 12 5 15 4 16 3;45 18 3;20 20 3 І так далі.
На додаток до таблиці інверсних значень, вавилоняни мали безліч інших таблиць: квадратів, кубів, квадратів і кубічних коренів і деяких інших.
Виклики
Які проблеми розв'язали вавилоняни?
Наприклад:
«10 братів і 1 цілих і 2/3 шахт срібла. Брат вищий, ніж брат. Я не знаю, скільки він є. Частка восьмого брата - 6 шекель. Наскільки вище брат над братом?
Завдання полягає в поділі суми між братами, щоб кожна частка є арифметичною прогресуванням і знайти різницю в цьому прогресуванні.
Звісно, вавилонський вирішив проблему за інтересами. Включаючи завдання на складні відсотки:
«Я виріс одну статую. У скільки років він виростає самостійно? « » » » » » » » » » » » » » »
Відсоток очікується 0;12 річних. Деякі дослідники запропонували, що вавилоняни володіли родзинками логарифмів. Інші не погоджуються з ними.
Ще один приклад включає квадрографічні рівняння:
« Площа двох квадратів додаємо, і це 37,5. З одного квадрата на 2/3 сторони іншої площі. 10 додано в сторону більшого, 5 додано в сторону менше. Ці квадрати які?
У таблицях ці завдання подаються з поясненням їх рішення. Ви можете побачити, що валоняни знали квадарні рівняння та системи лінійних рівнянь.
Вавилонський знала квадратні корені, які були розраховані за допомогою приблизних формул:
«Діагональ квадрата 10. Знайдіть бічну сторону квадрата. 10 з 0;42,30 множення 7;5 має бічну сторону. 7.5 з 1:25 множити. 10;25 це дає".
Джерело: geektimes.ru/post/252310/
Тепер я збираюся поговорити трохи про ще одну велику цивілізацію і культуру минулого. Вавилонський царства виник на початку 2-го тисячоліття до н.е., він замінив Sumer і Akkad і існував перед завоюванням персид у 539 р. до н.е. Написав в Вавилон, так як всі пам'ятають, на глиняних таблетках з туніформою, які дуже добре збережені на відміну від паперу, папірусу і аналогічних речей, тому ми знаємо досить багато про Вавилон, а про її математику. Ми не знаємо все. На відміну від греків, валоняни не залишають чітких алгоритмів або чітких пояснень їх техніки. Тепер ми можемо тільки вгадати, як саме вавилонський, діяв в цьому або тому випадку в вирішенні проблеми. У цій роботі я концентрую переважно на вавилонський арифметметику, залишивши при цьому геометрію, алгебра, астрономію.
Вавилонський просунувся набагато далі в математики, ніж єгиптяни, наскільки ми знаємо, хоча вони не збіглися з греками. Вони вже знали, як розв’язати квадарні рівняння, а також мали ряд об’єктів чисельної алгебри. Однією з їх досягнень стала запровадження позиційної шестивимірної системи номеру без нуля. Це означає, що обробка чисел стала набагато більш гнучкою і простою, ніж в Єгипті. Невідомо, що ця система з'явилася. Один варіант говорить про те, що він привів до змішування 6- і 10-річних систем людей Сумера і Akkad. Але є інші думки про це.
На жаль, ця система (і, можливо, не хотів би навчити їх багатозастосунковий стіл) не освоїлася іншими людьми Стародавнього світу, і ми повинні чекати прибуття індійської системи. Однак деякі відбиття вавилонської математики залишаються в нашій культурі: поділ хвилини на шістдесяти секунд і година в 60 хвилин є ехо давньої вавилонської системи.
Кількість номерів та номерна система
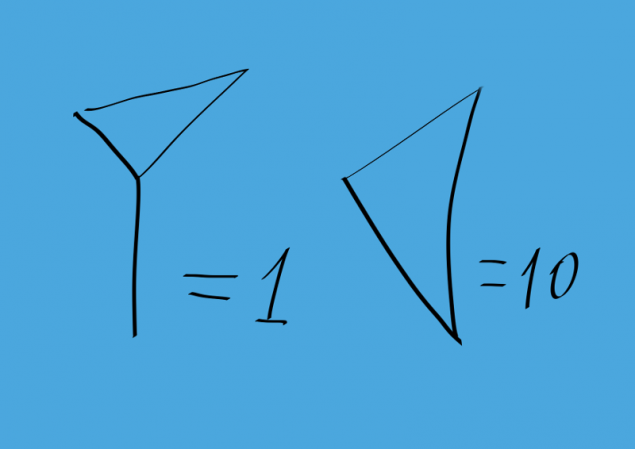
На малюнку показано, як валоняни позначені 1 і 10. Всі номери від 1 до 59 представлені. На малюнку нижче показано номер 33. Це схоже на римські та інші непозиційні системи написання номеру.
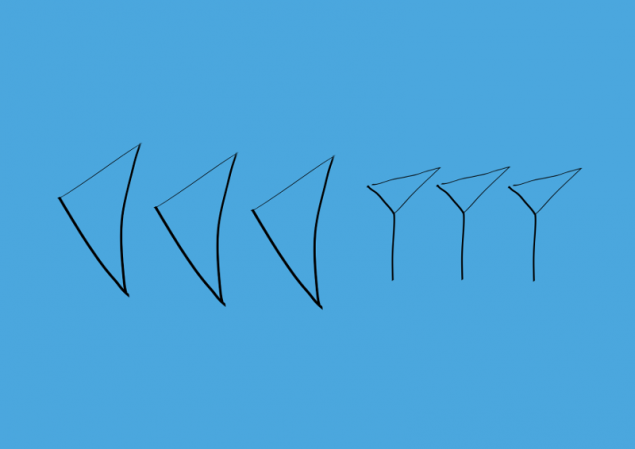 р.
р.Кількість 60 точно так само, як і один. На початку було намальовано більше, але пізніше ця відмінність була вилучена. Кількість номерів понад 60, але не менше 120, ніж 120, були занепадані наступним чином: спочатку було написано номер 60, потім решта кількості менше 60 було написано через простір.
Нижче наведено приклад No 63.

Кількість форм K*60+n (1<=K<60; n=1, 2, 3, ... 59) були позначені аналогією, як в прикладі нижче.
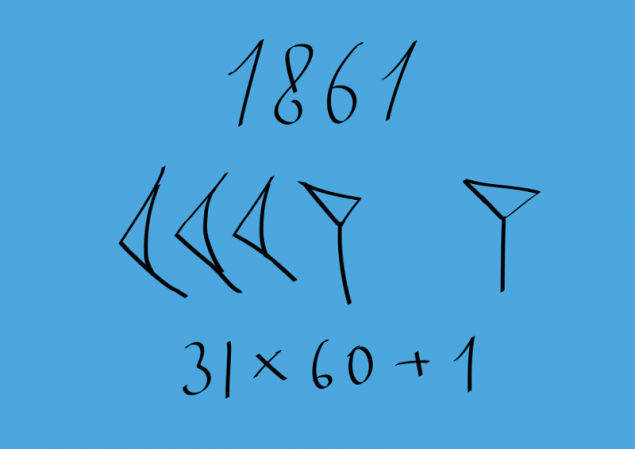
Вавилонський не мав 0, але з часом вони приходили до знака, що заперечували пропущені ряди. Ця ознака була використана тільки для укусів в межах числа і не була поставлена в кінці. Ось приклад на малюнку.
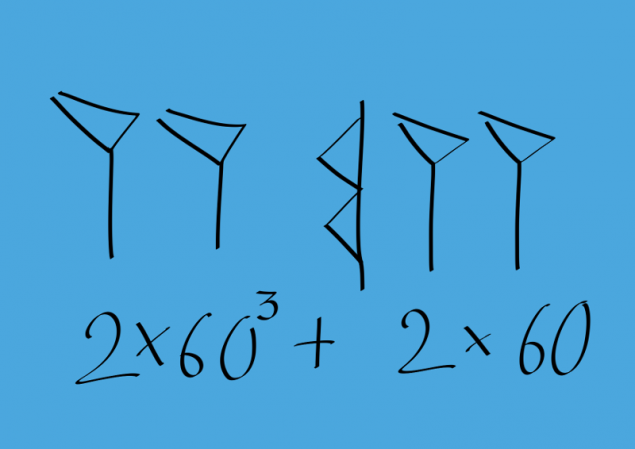
Проблема в тому, що цей номер може бути прочитаний як 2 * 60^2 +2, так і 2 * 60^5 +2 * 60^3. Дуже зручно! Ця система запису повинна призвести до численних помилок, які ви не думаєте? Вавилонський намагався дуже ретельно відокремити ряди, щоб уникнути сплутаності (міше ніж я зробив). У деяких випадках помилки дуже ймовірні. Приклади великих чисел відомі, коли частина номеру передається на іншу лінію. Спробуйте дізнатися, що ви означали! Але кількість помилок у валонських текстах невелика, хоча вони закінчуються.
Таким чином, вони також визначаються дроби. Тільки для дуже популярних 1/2, 1/3 і 2/3 були спеціальні іконки.
Девер я ходжу, я написаю валонські числа, розділяючи кому і всю частину від фракційного з півколоном. Наприклад: 177 є 2.57 і т.д. Змішані цифри, я замінив 0.
Розрахунок
Так як валонська система була позиціональною, їх розрахунки були схожими на нашу. При скороченні та додаванні вони просто додаються і відхилені числа трохи. Додаткова перевага була в тому, що шість цифр були денотовані в непозиційному вигляді за допомогою юнітів і десятків, і в такій системі набагато простіше відслідковувати і додати, ніж в наших абстрактних позначеннях, які вимагають вивчення особливої таблиці доповнення.
Багатокористування, як ви можете здогадатися, був схожий на наш. Але як вони використовують свій величезний багатозастосувальний стіл? Вивчивши це серцем? Вони приготували спеціальні столи, де вони могли дивитися роботи.
Багатофункціональні столи зійшли до нас з Вавилонян, але вони не включають в себе всі твори «єдиних» чисел, таких як наші десяткові столи. З 1 по 20 інклюзивних таблиць, з якими працює 30, 40, 50. Якщо вавилонський бажав розмножуватися 35 від 47, то йому довелося знайти в таблиці спочатку 35*40, а потім 35*7 і додати. Це вимагає додаткових дій, але таким чином можна було зберегти багато місця.
Вавилони не знали поділу як самостійна дія. замість цього вони використовували багатозастосування за зворотним номером. Для цього, звичайно, вони потрібні таблиці задніх чисел. Наприклад, якщо вам довелося розділити 1.15 на 5, Бабилонський знайдеться 1/5, що в їх записі буде 0;12 і множать 1.15 по 0;12. Якщо такий номер не був виражений скінченною шістдесятикратною дробою, то вавилоняни шукали номер, який, коли множили дивізором, дав дівидимість.
Наприклад, розділіть 22.45.0 на 6.30. Що потрібно взяти з 6.30, щоб отримати 22.45.0? Відповідь 3.30. Звісно, вавилоняни використовували приблизні значення при необхідності.
Неперевершені таблиці виглядають як це:
2 30 3 20 4 15 6 10 8 7;30 9 6;40 12 5 15 4 16 3;45 18 3;20 20 3 І так далі.
На додаток до таблиці інверсних значень, вавилоняни мали безліч інших таблиць: квадратів, кубів, квадратів і кубічних коренів і деяких інших.
Виклики
Які проблеми розв'язали вавилоняни?
Наприклад:
«10 братів і 1 цілих і 2/3 шахт срібла. Брат вищий, ніж брат. Я не знаю, скільки він є. Частка восьмого брата - 6 шекель. Наскільки вище брат над братом?
Завдання полягає в поділі суми між братами, щоб кожна частка є арифметичною прогресуванням і знайти різницю в цьому прогресуванні.
Звісно, вавилонський вирішив проблему за інтересами. Включаючи завдання на складні відсотки:
«Я виріс одну статую. У скільки років він виростає самостійно? « » » » » » » » » » » » » » »
Відсоток очікується 0;12 річних. Деякі дослідники запропонували, що вавилоняни володіли родзинками логарифмів. Інші не погоджуються з ними.
Ще один приклад включає квадрографічні рівняння:
« Площа двох квадратів додаємо, і це 37,5. З одного квадрата на 2/3 сторони іншої площі. 10 додано в сторону більшого, 5 додано в сторону менше. Ці квадрати які?
У таблицях ці завдання подаються з поясненням їх рішення. Ви можете побачити, що валоняни знали квадарні рівняння та системи лінійних рівнянь.
Вавилонський знала квадратні корені, які були розраховані за допомогою приблизних формул:
«Діагональ квадрата 10. Знайдіть бічну сторону квадрата. 10 з 0;42,30 множення 7;5 має бічну сторону. 7.5 з 1:25 множити. 10;25 це дає".
Джерело: geektimes.ru/post/252310/























