1484
于是想到了古人。巴比伦
这是一个延续怀我对一系列计算和账户的历史。这里埃及的第一篇文章。
现在,我会尽量谈一些关于过去的其他伟大的文明和文化。巴比伦王国出现的前2千纪的开始,它已经取代了苏美尔阿卡德和,和波斯在公元前539年征服之前就存在他们写道:在巴比伦,大家都还记得,泥板上的楔形文字与使用保存得非常完好,不像纸,纸莎草,之类的东西,所以我们知道了很多关于和巴比伦和他的数学。但是,当然,我们不知道的一切。不同的是希腊人,巴比伦人已经离开了精确算法和它的方法解释清楚。现在,我们只能猜测如何巴比伦人的行为在特定情况下解决问题。在本文中,我主要sosredtochus在巴比伦算术,撇开几何,代数和天文学。
巴比伦人在数学上的进展远远超出了埃及人,因为我们知道,但没有赶上与希腊人,显然。他们已经知道如何解决二次方程,除了有数值代数的一些雏形。他们的一个成果是引入位置的六十进位无划痕。这意味着,与数字处理变得更加灵活和比埃及简单。只是不知道它是从哪里来的这样一个系统。其中一个版本说,它已造成6元和苏美尔阿卡德和各国人民的10进制系统的混合物。但也有关于这个问题的其他想法。
这个系统,不幸的是(或许幸运的是,不希望教他们乘法表)并不适用于古代世界的其他国家,而不得不等待印度定位系统的到来。然而,一些反映巴比伦数学在我们的文化遗存:每小时分钟的划分,六十秒〜60分钟 - 古巴比伦数字系统的回声
。
数字和数字系统
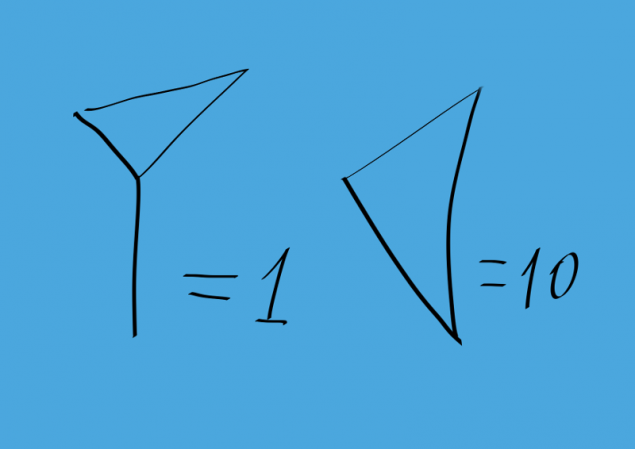
图为如何巴比伦人是1和10有了他们的帮助,描绘所有的号码从1到59下图为33号这是类似罗马和数字书写等nonpositional系统。
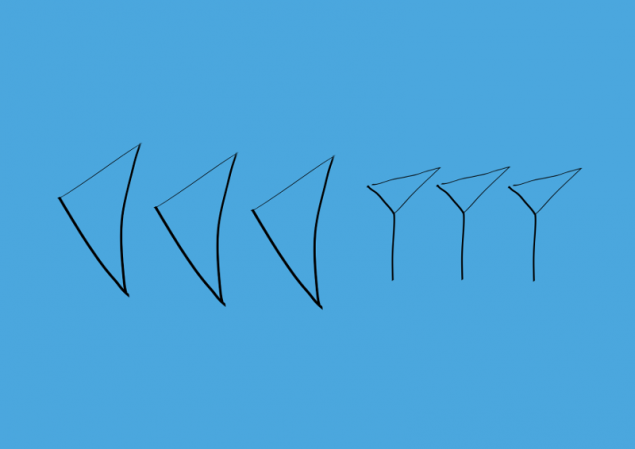
号60恰好表示为一个单元。在开始的时候被画大,但后来删除了区分。数大于60,但小于120被指定如下:首先写入编号60和编号的再通过间隙的其余部分,较小60.
下面是63
一例

形式的数字的 K * 60 + N(1&其中; = K&其中; 60; n = 1时,2,3,...... 59)。 i>的类推指定,如在下面的例子
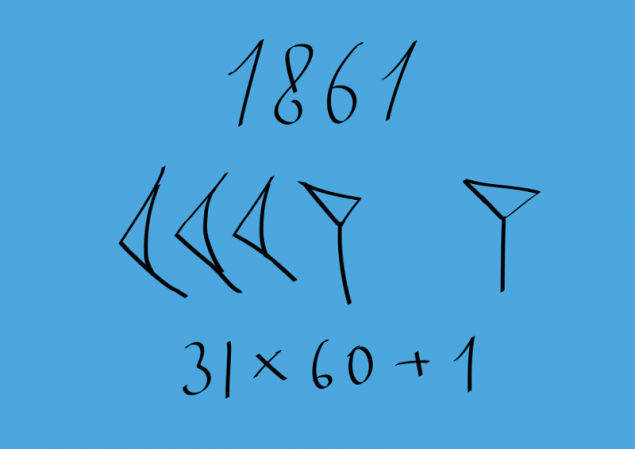
巴比伦人不为0的,但随着时间的推移,他们想出了用这意味着丢失位的标志。该标志仅适用于内的比特数,并没有提出在末端。这里是在画面的一个例子。
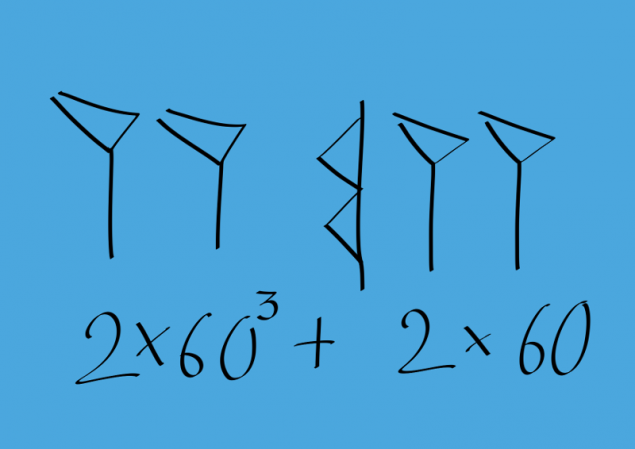
的问题是,这个数字可以被读出和2 * 60 ^ 2 2,和2 * 60 ^ 5 + 2 * 60 ^ 3。很不舒服!该记录系统将有导致许多错误,你不觉得吗?巴比伦人尝试非常仔细地分开排放,以避免混乱(更整洁比我)。然而,在某些情况下,误差是非常可能的。有大量的例子,当部件号转移到另一条线路。揣摩出在这里,这意味着!但错误的巴比伦文字的数量很少,虽然他们是在那里。
相同的方法被指定和分数。只有一个非常受欢迎的1/2,1/3和2/3是特殊的徽章。
无处不在我将继续记录巴比伦的数量,分离燃放点,并用分号分数的整数部分。例如:177为2,57,等等。错过了水平,我将取代0
计算
由于该系统是一个位置巴比伦人,他们的计算是rchen与我们相似。当加减,他们只是添加和数字减去的数字位数。一个附加的优点是,该六十进制数字表示nonpositional方式由1和数十,以及在这种系统中减去,并添加比在我们的抽象符号需要特殊表学习除了要容易得多。
乘法,您可能已经猜到,也就是类似于我们的。但他们用自己的庞大的乘法表?他们教它由心脏?他们准备的特殊表,你可以看的工作。
从巴比伦人生存了许多乘法表,但他们并没有包括“明确的”号码为十进制我们的表中的所有作品。他们的桌子开始从1至20包容,再接着的30,40,50。如果巴比伦人想用47乘以35,他只好找前35 * 40的表,那么35 * 7和折叠的作品。这需要额外的行动,但这样能显著节省空间。
司作为一个独立的行动巴比伦人不知道。相反,它们用于相乘的倒数。要做到这一点,当然,他们所需要的表倒数。例如,如果有必要,以划分1 15 5 1/5巴比伦发现他们的记录将是我们0; 12和乘1,15至0; 12。如果这个数字并不表示最后六十进制分数,巴比伦人正在寻找一个数字,当除数乘以分红了。
例如,你把22,45,0 6,30在这种情况下,这样的条件是说:“那我需要带6,30〜22弄,45,0? “答案是3,30,当然,巴比伦人用来和近似值在需要的时候。
表倒数如下:
2 TD> 30 TD> TR> 3 TD> 20 TD> TR> < TR> 4 TD> 15 TD> TR> 5 TD> 12 TD> TR> 6 TD> 10 TD> TR> 8 TD> 7; 30 TD> TR> 9 TD> 6; 40 TD> TR> 12 TD> 5 TD> TR> 15 TD> 4 TD> TR> 16 TD> 3; 45 TD> TR> 18 TD> 3。20 TD> TR> 20 TD> 3 TD> TR> TABLE>等等
除了逆值表,巴比伦人有许多其他表:正方形,立方体,方形和立方根,和其他一些人。
任务
有什么问题可以解决巴比伦人?
例如,这样的方法:
“10个兄弟和1 2/3全和银矿。大哥二哥以上。只要它是较高的,我不知道。分享第八兄弟6谢克尔。在哥的弟弟高出多少? “ I>
的目标是将兄弟之间的总和,使得算术级数的各成分的比例,并找到了进展的差异。
当然,巴比伦人和解决的利益问题。包括复利问题:
“一个GUR他给了增长。经过多少年它会自己成长吗?“ I>
假设百分比0; 12年息。一些研究人员认为,巴比伦人拥有对数的开端。别人不同意他们。
另一个例子包括二次方程:
«桩的两个平方的面积,并且它是37,5一侧的正方形的是另一种方2/3。 10更多的人,除了在一旁补充说,以较小的5边加入除。这些方块是什么?» I>
在表中,这些问题都与他们的决定的说明。由此可以看出,该巴比伦人已知二次方程和线性方程系统。
做了巴比伦人和平方根,这是用近似公式计算:
“对角广场上有10找到一个正方形的边。 10比0,42,30乘以7,5,有一个党。 7,5,1; 25繁殖。 10和25也给出了“。
来源: geektimes.ru/post/252310/
现在,我会尽量谈一些关于过去的其他伟大的文明和文化。巴比伦王国出现的前2千纪的开始,它已经取代了苏美尔阿卡德和,和波斯在公元前539年征服之前就存在他们写道:在巴比伦,大家都还记得,泥板上的楔形文字与使用保存得非常完好,不像纸,纸莎草,之类的东西,所以我们知道了很多关于和巴比伦和他的数学。但是,当然,我们不知道的一切。不同的是希腊人,巴比伦人已经离开了精确算法和它的方法解释清楚。现在,我们只能猜测如何巴比伦人的行为在特定情况下解决问题。在本文中,我主要sosredtochus在巴比伦算术,撇开几何,代数和天文学。
巴比伦人在数学上的进展远远超出了埃及人,因为我们知道,但没有赶上与希腊人,显然。他们已经知道如何解决二次方程,除了有数值代数的一些雏形。他们的一个成果是引入位置的六十进位无划痕。这意味着,与数字处理变得更加灵活和比埃及简单。只是不知道它是从哪里来的这样一个系统。其中一个版本说,它已造成6元和苏美尔阿卡德和各国人民的10进制系统的混合物。但也有关于这个问题的其他想法。
这个系统,不幸的是(或许幸运的是,不希望教他们乘法表)并不适用于古代世界的其他国家,而不得不等待印度定位系统的到来。然而,一些反映巴比伦数学在我们的文化遗存:每小时分钟的划分,六十秒〜60分钟 - 古巴比伦数字系统的回声
。
数字和数字系统
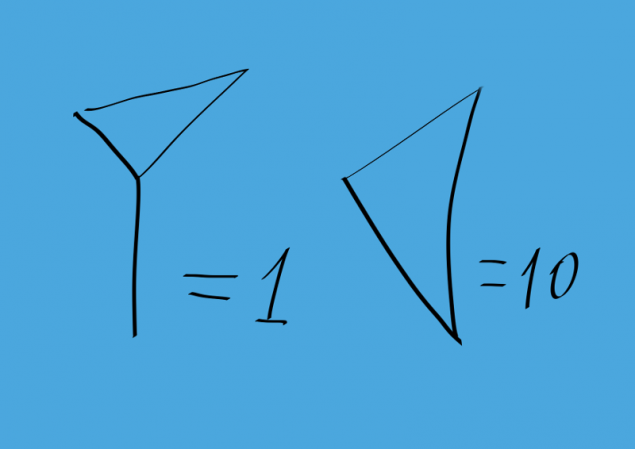
图为如何巴比伦人是1和10有了他们的帮助,描绘所有的号码从1到59下图为33号这是类似罗马和数字书写等nonpositional系统。
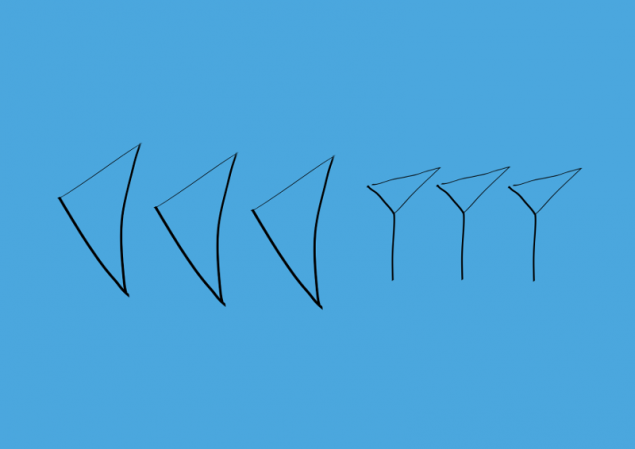
号60恰好表示为一个单元。在开始的时候被画大,但后来删除了区分。数大于60,但小于120被指定如下:首先写入编号60和编号的再通过间隙的其余部分,较小60.
下面是63
一例

形式的数字的 K * 60 + N(1&其中; = K&其中; 60; n = 1时,2,3,...... 59)。 i>的类推指定,如在下面的例子
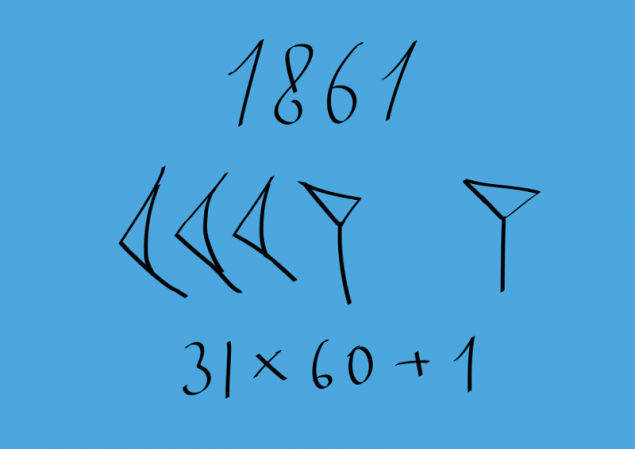
巴比伦人不为0的,但随着时间的推移,他们想出了用这意味着丢失位的标志。该标志仅适用于内的比特数,并没有提出在末端。这里是在画面的一个例子。
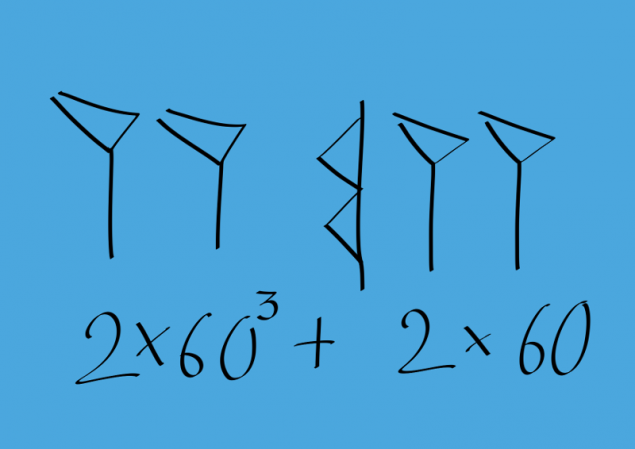
的问题是,这个数字可以被读出和2 * 60 ^ 2 2,和2 * 60 ^ 5 + 2 * 60 ^ 3。很不舒服!该记录系统将有导致许多错误,你不觉得吗?巴比伦人尝试非常仔细地分开排放,以避免混乱(更整洁比我)。然而,在某些情况下,误差是非常可能的。有大量的例子,当部件号转移到另一条线路。揣摩出在这里,这意味着!但错误的巴比伦文字的数量很少,虽然他们是在那里。
相同的方法被指定和分数。只有一个非常受欢迎的1/2,1/3和2/3是特殊的徽章。
无处不在我将继续记录巴比伦的数量,分离燃放点,并用分号分数的整数部分。例如:177为2,57,等等。错过了水平,我将取代0
计算
由于该系统是一个位置巴比伦人,他们的计算是rchen与我们相似。当加减,他们只是添加和数字减去的数字位数。一个附加的优点是,该六十进制数字表示nonpositional方式由1和数十,以及在这种系统中减去,并添加比在我们的抽象符号需要特殊表学习除了要容易得多。
乘法,您可能已经猜到,也就是类似于我们的。但他们用自己的庞大的乘法表?他们教它由心脏?他们准备的特殊表,你可以看的工作。
从巴比伦人生存了许多乘法表,但他们并没有包括“明确的”号码为十进制我们的表中的所有作品。他们的桌子开始从1至20包容,再接着的30,40,50。如果巴比伦人想用47乘以35,他只好找前35 * 40的表,那么35 * 7和折叠的作品。这需要额外的行动,但这样能显著节省空间。
司作为一个独立的行动巴比伦人不知道。相反,它们用于相乘的倒数。要做到这一点,当然,他们所需要的表倒数。例如,如果有必要,以划分1 15 5 1/5巴比伦发现他们的记录将是我们0; 12和乘1,15至0; 12。如果这个数字并不表示最后六十进制分数,巴比伦人正在寻找一个数字,当除数乘以分红了。
例如,你把22,45,0 6,30在这种情况下,这样的条件是说:“那我需要带6,30〜22弄,45,0? “答案是3,30,当然,巴比伦人用来和近似值在需要的时候。
表倒数如下:
2 TD> 30 TD> TR> 3 TD> 20 TD> TR> < TR> 4 TD> 15 TD> TR> 5 TD> 12 TD> TR> 6 TD> 10 TD> TR> 8 TD> 7; 30 TD> TR> 9 TD> 6; 40 TD> TR> 12 TD> 5 TD> TR> 15 TD> 4 TD> TR> 16 TD> 3; 45 TD> TR> 18 TD> 3。20 TD> TR> 20 TD> 3 TD> TR> TABLE>等等
除了逆值表,巴比伦人有许多其他表:正方形,立方体,方形和立方根,和其他一些人。
任务
有什么问题可以解决巴比伦人?
例如,这样的方法:
“10个兄弟和1 2/3全和银矿。大哥二哥以上。只要它是较高的,我不知道。分享第八兄弟6谢克尔。在哥的弟弟高出多少? “ I>
的目标是将兄弟之间的总和,使得算术级数的各成分的比例,并找到了进展的差异。
当然,巴比伦人和解决的利益问题。包括复利问题:
“一个GUR他给了增长。经过多少年它会自己成长吗?“ I>
假设百分比0; 12年息。一些研究人员认为,巴比伦人拥有对数的开端。别人不同意他们。
另一个例子包括二次方程:
«桩的两个平方的面积,并且它是37,5一侧的正方形的是另一种方2/3。 10更多的人,除了在一旁补充说,以较小的5边加入除。这些方块是什么?» I>
在表中,这些问题都与他们的决定的说明。由此可以看出,该巴比伦人已知二次方程和线性方程系统。
做了巴比伦人和平方根,这是用近似公式计算:
“对角广场上有10找到一个正方形的边。 10比0,42,30乘以7,5,有一个党。 7,5,1; 25繁殖。 10和25也给出了“。
来源: geektimes.ru/post/252310/























