的165年历史的任务是闹鬼的数学家

1850年牧师托马斯·柯克曼，英国数学家和兰开夏郡教区的神父，制定了娱乐杂志的数学爱好者“笔记本电脑女士们先生们»一个无辜的前瞻性拼图：

“十五年轻女生去散步七天行之三：你每天需要将它们放置，使同一对女学生从来没有在连续»举行了两次会议
。
这个任务看起来很简单，但如果你试图解决它，你立刻意识到这是不是这样。你可以尝试用铅笔和纸来解决它或播放<一href="https://www.quantamagazine.org/20150609-the-nine-schoolgirls-challenge/">HTML-версию.

由于其简单的假问题迅速成名。他决定派出数学爱好者和科学家们试图制定一个共同的解决问题的方法发表的研究论文。

这样一来，这个难题已经帮助形成数学的一个新的分支：组合电路，谁现在致力于<一个href="https://books.google.by/books/about/Combinatorial_Design_Theory.html?id=SWO2bQ1HVbIC&redir_esc=y">толстые教科书的。什么开始作为分配到的人群（或方案，结果他们被称为）一个简单的任务，现在已经成为用于在实验设计的方法，在计算机科学，密码学，农业，体育，甚至是欺诈赌博纠错码（这个故事是，当犯罪卡特尔已经赢得了数百万美元的七年，买票用5所有可能组合出46的彩票6出46，如果门票价格比额外的奖金中奖5，满分46低，再加上赢得大奖的概率。）< BR />
例如，对于纠错古典海明代码使用的问题关于女生的溶液（三女学生创建组，在没有对非经常性），但只有到的七个女孩（比特）的方案。



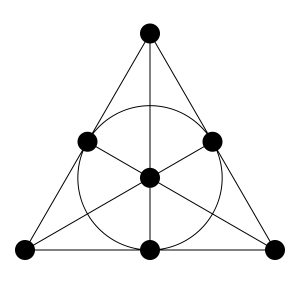
平面法诺（7，3，2） I>

最令人惊讶的是，在该165年数学一直没能解决的问题在一般的方式。他们仍然不能回答，如何解决在拼图的初始条件：有名词 i>的女生需要创建 K i>的一组大小，从而使集 T 我>女孩子从来没有在同一个组举行了两次会议。这一提法被称为方案（N，K，T） I>。

例如，对于一组的19名妇女有超过11十亿，其中每一对被发现只有一次可能三胞胎。这个数字是答案。但是选项的数量呈指数级增长作为女生的数量。

很显然，该问题是在某些条件下解决了，并且不能在其他一些解决。例如，如果六个写所有可能的成对的女生三胞胎，显而易见的问题不解决（共女生安娜，有五种可能的对，同时在每一三元组有两对与安娜，除了五个不除以二）。这是整除的原则，立即筛选出很多选择（N，K，T） I>。

与此同时，也有（N，K，T） i>的，这是与可分的原则是一致的，但仍然没有解决：例如，（47，3，2） I>。

在过去的几年中，决定出名许多组合（N，K，T） I>，已代数或枚举验证的计算机上。但如何解决这个在一般的方式做什么用的异常如（47，3，2） I>？如何理解，它是决策与否的任务？

这个问题一直被认为是在组合学，<一个最著名的问题之一href="http://www.wired.com/2015/06/answer-150-year-old-math-conundrum-brings-mystery/">говорит数学家卡莱吉尔（GIL卡莱）在耶路撒冷希伯来大学的，在有线的专访。他记得争论这个与同事和年半前，他们得出结论说：“我们永远不会知道答案，因为这个问题显然过于复杂»。

然而，从牛津大学只有两个星期的数学彼得Kivash （彼得Keevash）的年轻教授表明，卡莱错误。从2014年1月的科学文章，他认为，解决方案几乎总是存在的，如果整除的条件。 href="http://arxiv.org/pdf/1504.02909v1.pdf">新工作从2015年4月，他展示了如何计算给定参数解决方案的大致数量的
谁也没有料到，要解决这个问题，你可以申请概率理论，但该方法得很完美。

回到彩票，骗子已经意识到，有可能减少购买门票的数量，如果买了5所有组合出46（如果指定6 46号），他们将获得额外的奖品应有尽有，但仍然可以得到大奖。虽然该方案的（46，6,5） i>的未计算，但也有方案是足够接近实际应用。其中之一很可能已经使用了一个犯罪卡特尔。

新方案的一些旨在不断增加。他们中很多实际应用为（7，3，2） i>和（46，6，5） I>。快来一起计划1000页的目录。然而，数学仍推测以确定是否有用于特定的一组条件的溶液。感谢Kivashu我们了解到，这个概率是相当高的。所以至少现在是明确的，对于所有的未知看起来比放弃更好的解决方案。此外，也有工具来生成近似 i>的方案进行任何参数。

但由于工作Kivasha有希望，我们可以开发一个方法来创建一个确切 i>的方案为所有参数。如果出现这种情况，这将是在数学非凡的突破。

然而，工作是纯理论Kivasha。专家说，建立他的方法的基础上，实际的机制将需要几代数学家的更辛苦。

来源： geektimes.ru/post/252308/