La tarea de los 165 años de edad, es matemáticos embrujadas

En 1850 el reverendo Thomas Kirkman, el matemático británico y rector de la parroquia, en Lancashire, ha formulado un rompecabezas de aspecto inocente en la revista de entretenimiento para los amantes de las matemáticas "damas y caballeros» Notebook:

"Quince jóvenes colegialas van a dar un paseo por siete días en filas de tres: que necesita cada día para colocarlos de manera que el mismo par de colegialas nunca se reunió dos veces en una fila»
.
La tarea parece simple, pero si tratas de resolverlo, que de inmediato se da cuenta que esto no es así. Usted puede tratar de resolverlo con lápiz y papel o jugar HTML-версию.

Debido a su simplicidad falsa problema rápidamente se hizo famoso. Su decisión envió amantes de las matemáticas, y los científicos han publicado artículos de investigación en un intento de formular una solución común al problema.

Como resultado, este rompecabezas ha ayudado a formar una nueva rama de las matemáticas: circuito combinatorio, que ahora se dedica a толстые libros de texto . Lo que comenzó como una tarea sencilla para su distribución a grupos de personas (o esquemas como resultado se les llamaba), ahora se ha convertido en el método que se utiliza en el diseño experimental, los códigos de corrección de errores en ciencias de la computación, la criptografía, la agricultura, el deporte, e incluso los juegos de azar fraude (la historia fue cuando el cártel criminal ha ganado millones de dólares en siete años, la compra de billetes con todas las combinaciones posibles de 5 sobre 46 en la lotería de 6 de cada 46 si el precio de la entrada era más bajo que los bonos adicionales para ganar 5 sobre 46, más la probabilidad de ganar el premio mayor.) < br />
Por ejemplo, el código de Hamming clásica para corrección de errores utiliza una solución del problema de las colegialas (crear grupos de tres colegialas, donde ningún par de no recurrente), pero sólo con el esquema de las siete niñas (bits).



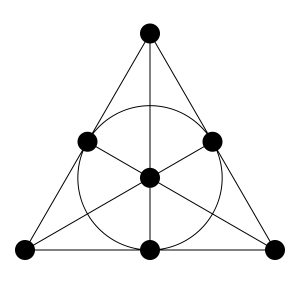
El avión Fano (7, 3, 2) i>

Lo más sorprendente de todo es que en los 165 años de las matemáticas no han sido capaces de resolver el problema de una manera general. Ellos todavía no pueden contestar, ¿cuál es la solución en el rompecabezas de las condiciones iniciales: hay n i> colegialas Necesito crear un tamaño de grupo de k i>, de modo que el conjunto de t i> las niñas nunca había reunido dos veces en el mismo grupo. Esta formulación se llama esquema (n, k, t) i>.

Por ejemplo, para un grupo de 19 mujeres con más de 11 mil millones de tripletes posibles en el que cada par se encuentra sólo una vez. Este número es la respuesta. Pero el número de opciones está creciendo exponencialmente a medida que el número de alumnas.

Está claro que el problema se resuelve en determinadas condiciones y no puede ser resuelto en algún otro. Por ejemplo, si seis escribir colegialas tripletes de todos los posibles pares, el problema obvio no está resuelto (co colegiala Anna, hay cinco pares posibles, al mismo tiempo en cada triplete tiene dos pares con Anna, pero cinco no se divide por dos). Ese es el principio de la divisibilidad inmediatamente descartadas muchas opciones (n, k, t) i>.

Al mismo tiempo, hay (n, k, t) i>, que son consistentes con el principio de la divisibilidad, pero aún no tienen solución: por ejemplo, (47, 3, 2) i>.

En los últimos años, la decisión se dio a conocer a muchas combinaciones de (n, k, t) i>, que han sido verificados algebraicamente o recuento en las computadoras. Pero la forma de resolver esto de una manera general, qué hacer con excepciones como (47, 3, 2) i>? ¿Cómo entender, es la tarea de la decisión o no?

Este problema ha sido considerado como uno de los problemas más famosos de la combinatoria, говорит matemático Gil Kalai (Gil Kalai) de la Universidad Hebrea de Jerusalén, en una entrevista con Wired. Recuerda discutir sobre esto con colegas y hace año y medio, y se llegó a la conclusión de que "Nunca sabremos la respuesta, porque el problema es claramente demasiado complicado».

Sin embargo, apenas dos semanas el joven profesor de matemáticas Peter Kivash (Peter Keevash) de Oxford demostraron que Kalai mal. El artículo científico de enero de 2014, sostiene que la solución es casi siempre allí, si la condición de la divisibilidad. El nueva trabajo a partir de abril de 2015, que mostró cómo calcular el número aproximado de soluciones para los parámetros dados.

Nadie esperaba que para resolver el problema, se puede aplicar la teoría de la probabilidad, pero el método ha funcionado a la perfección.

Volviendo a la lotería, los estafadores se han dado cuenta de que es posible reducir el número de billetes adquiridos, si comprar todas las combinaciones de 5 sobre 46 (si especifica 6 de 46 números), recibirán premios adicionales de todo, pero todavía puede obtener el premio mayor. Aunque el esquema de (46, 6, 5) i> no se calcula, pero hay planes de que sean lo suficientemente cerca como para que la aplicación práctica. Uno de ellos es probable que hayan usado un cártel criminal.

El número de nuevos esquemas diseñados en constante crecimiento. Muchos de ellos encontrar aplicación práctica como (7, 3, 2) i> y (46, 6, 5) i>. Venga 1000 directorios de páginas con los esquemas. Sin embargo, las matemáticas todavía se especula como para determinar si hay una solución para un conjunto específico de condiciones. Gracias Kivashu nos enteramos de que la probabilidad de que esto es bastante alto. Así que por lo menos ahora, está claro que para todas las incógnitas se ven mejor solución que abandonarla. Por otra parte, hay herramientas para generar los aproximadas i> esquemas para cualquier parámetro.

Pero gracias al trabajo Kivasha tienen esperanza de que podamos desarrollar un método para crear un exactas i> esquemas para todos los parámetros. Si eso sucede, será un avance extraordinario en la matemática.

Sin embargo, el trabajo es Kivasha puramente teórico. Los expertos dicen que la creación de mecanismos prácticos sobre la base de su método requerirá más esfuerzo de varias generaciones de matemáticos.

Fuente: geektimes.ru/post/252308/