1487
Así pensaban los antiguos. Babilonia
Esta es una continuación me concibió sobre la historia de la serie de cálculos y cuentas. El primer artículo sobre Egipto href="http://geektimes.ru/post/240900/#first_unread">.
Ahora voy a tratar de hablar un poco sobre la otra gran civilización y la cultura del pasado. Reino babilónico surgió a principios del segundo milenio antes de Cristo, que ha sustituido a Sumer y Akkad, y existía antes de la conquista de Persia en el 539 aC Escribieron en Babilonia, como todos recordamos, en tablillas de arcilla con escritura cuneiforme usar ese muy bien conservado, a diferencia del papel, papiro, y cosas por el estilo, así que saben mucho y sobre Babilonia, y sobre sus matemáticas. Pero, por supuesto, no lo sabemos todo. A diferencia de los griegos, los babilonios han dejado los algoritmos exactos y clara explicación de sus métodos. Ahora sólo podemos adivinar cómo los babilonios actuar en un caso particular, para resolver el problema. En este trabajo me sosredtochus principalmente en la aritmética babilónica, dejando de lado la geometría, el álgebra y astronomía.
Los babilonios en matemáticas progresado mucho más allá de los egipcios, como la conocemos, pero no alcanzó a los griegos, al parecer. Ellos ya saben cómo resolver ecuaciones de segundo grado, además tenía algunos rudimentos de álgebra numérica. Uno de sus logros fue la introducción de sexagesimal posicional sin un rasguño. Esto significa que el tratamiento con los números a ser mucho más flexible y más simple que en Egipto. Simplemente no sé de dónde vino ese sistema. Una versión dice que ha dado lugar a una mezcla de sistemas de 10-arias de los pueblos de Sumer y Akkad 6-aria y. Pero hay otras ideas sobre este tema.
Este sistema, por desgracia (quizás afortunadamente, no quiero enseñarles las tablas de multiplicar) no era aplicable a otras naciones del mundo antiguo, y tuvo que esperar a la llegada del sistema posicional indio. Sin embargo, lo que refleja las matemáticas babilónicas en nuestra cultura sigue siendo: la división de minutos por hora, sesenta segundos y 60 minutos - un eco del antiguo sistema de numeración babilónica
.
Los números y el
sistema numérico
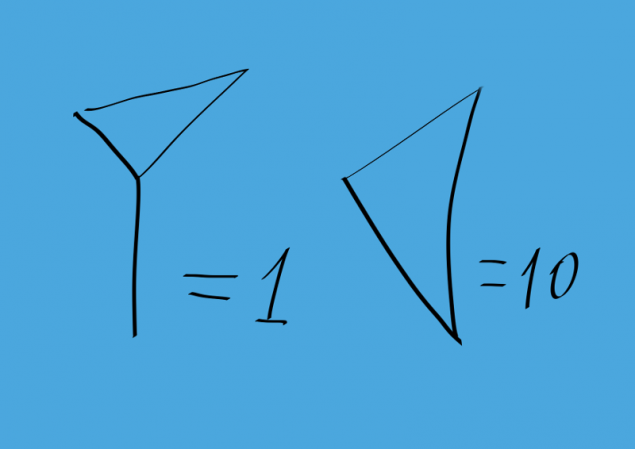
La imagen muestra cómo los babilonios es 1 y 10. Con su ayuda, retrata todos los números del 1 al 59. El cuadro siguiente muestra el número 33. Esto es similar a la romana y otro sistema nonpositional de escribir los números.
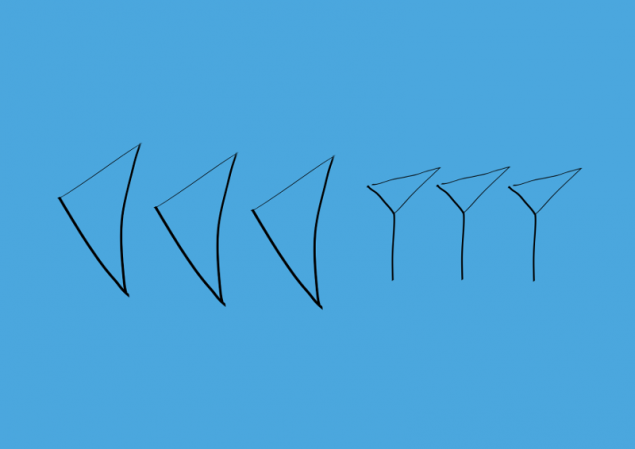
El número 60 expresó exactamente como una unidad. En el principio fue dibujado más grande pero más tarde borró esa distinción. Números mayores que 60 pero menor que 120 se designan como sigue: número 60 escrito primero, y luego a través de la brecha el resto del número, el más pequeño 60.
A continuación se muestra un ejemplo de 63

Los números de la forma K * 60 + n (1 & lt; = K & lt; 60; n = 1, 2, 3, ... 59). I> designado por analogía, como en el ejemplo siguiente
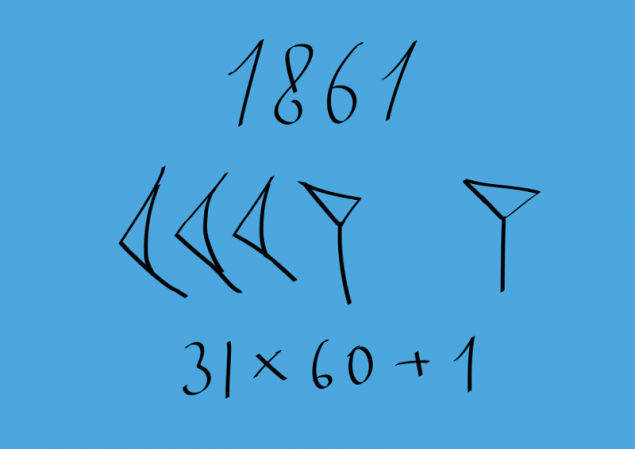
Los babilonios no eran 0, pero con el tiempo se le ocurrió utilizar una señal de lo que significaba trozos faltantes. Esta marca sólo se aplica al número de bits en el interior y no se planteó al final. He aquí un ejemplo en la imagen.
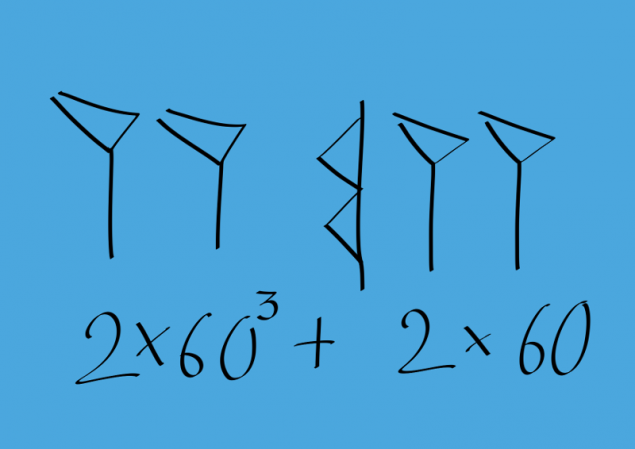
El problema es que este número podría ser leído y como 2 * 60 ^ 2 2, y como 2 * 60 ^ 5 + 2 * 60 ^ 3. Muy incómodo! Este sistema de grabación tendría lugar a numerosos errores, ¿no crees? Los babilonios trataron con mucho cuidado para separar las descargas para evitar confusiones (mucho más ordenado que yo). Sin embargo, en algunos casos, es muy probable que el error. Hay ejemplos de grandes números cuando el número de parte transferida a otra línea. Trate de averiguar aquí, eso significa! Pero el número de errores en los textos babilónicos es pequeña, a pesar de que están allí.
El mismo método fue designada y fracciones. Sólo un muy popular 1/2, 1/3 y 2/3 eran insignias especiales.
Dondequiera que voy a seguir para registrar el número de Babilonia, que separa el punto de descarga y parte entera de la fracción con un punto y coma. Por ejemplo: 177 es 2, 57, etc. Nivel Perdidas, voy a sustituir a 0.
Cálculos
Dado que el sistema era una posición babilonios, sus cálculos eran rchen similar a la nuestra. Cuando la suma y la resta, que acaba de sumar y restar números dígito por dígito. Una ventaja adicional fue que los dígitos sexagesimales indican de manera nonpositional por unidades y decenas, y en tal sistema para restar y añadir mucho más fácil que en nuestra notación abstracta que requiere mesa especial aprender adición.
Multiplicación, como puede imaginar, también, fue similar a la nuestra. Pero ellos usaron su vasta tabla de multiplicar? Enseñaron de memoria? Ellos se prepararon mesas especiales donde se puede ver la obra.
De los babilonios que ha sobrevivido muchas tablas de multiplicar, pero no incluyen todas las obras de números "inequívocas" como decimal nuestra mesa. Su tabla comienza de 1 a 20 inclusive, a continuación, seguido de las obras de 30, 40, 50. Si los babilonios querían multiplicar 35 por 47, que tenía que encontrar una mesa primero 35 * 40, entonces 35 * 7 y doblar. Esto requiere una acción adicional, pero también lo podría ahorrar significativamente el espacio.
División como una acción independiente babilonios no conocían. En su lugar, utilizan la multiplicación por el número inverso. Para ello, por supuesto, que necesitaban los números inversos de mesa. Por ejemplo, si era necesario dividir 1 15 5 1/5 babilónico encontró que sus registros serán nuestro 0; 12 y multiplicar 1, 15 a 0, 12. Si este número no expresa una fracción sexagesimal final, los babilonios buscando un número que multiplicado por el divisor dio dividendos.
Por ejemplo, se divide 22, 45, 0 6, 30. En este caso, tal condición se afirma: "¿Qué tengo que tomar 6, 30 para obtener 22, 45, 0? "La respuesta es 3, 30. Por supuesto, los babilonios utilizaban y valores aproximados cuando sea necesario.
Tablas recíprocos aspecto:
2 30 3 20 < 4 15 5 12 6 10 8 7; 30 9 6; 40 12 5 15 4 16 3; 45 18 3;. 20 20 3 Y así sucesivamente
Además de la tabla de valores inversos, los babilonios tenían muchas otras tablas: cuadrados, cubos, raíces cuadradas y cúbicas, y algunos otros.
Tareas
¿Qué problemas podría resolver los babilonios?
Por ejemplo, como:
"10 hermanos y 1 2/3 enteros y plata minas. Hermano hermano anteriormente. Por lo que es más alto, yo no lo sé. Comparte octavo hermano 6 shekels. Brother en hermano de la cantidad más alta? " I>
El objetivo es dividir la suma entre los hermanos de modo que la proporción de cada componente de una progresión aritmética y para encontrar la diferencia de la progresión.
Por supuesto, los babilonios y resuelve el problema de los intereses. Incluyendo problemas en el interés compuesto:
"Una gur le di al crecimiento. ¿Después de cuántos años va a crecer por sí mismo? " I>
Porcentaje asumió 0; 12 por año. Algunos investigadores han sugerido que los babilonios poseían los inicios de los logaritmos. Otros están en desacuerdo con ellos.
Otro ejemplo incluye ecuaciones cuadráticas:
«La zona de las dos plazas de la pila, y es 37, 5. lateral de la plaza es de 2/3 de otra plaza. 10 más se añadieron además a un lado, al lado de la más pequeña 5 se añadieron además. Estas plazas son eso? » I>
En las tablas, estos problemas son con la explicación de su decisión. Se puede observar que los babilonios conocidos ecuaciones cuadráticas y el sistema de ecuaciones lineales.
¿Los babilonios y raíces cuadradas, que se calcularon utilizando las fórmulas aproximadas:
"Cuadrado Diagonal tiene 10. Encuentra el lado de un cuadrado. 10 a 0, 42, 30 multiplicar el 7, 5, tener una fiesta. 7, 5, 1; 25 a multiplicar. 10 y 25 se da ".
Fuente: geektimes.ru/post/252310/
Ahora voy a tratar de hablar un poco sobre la otra gran civilización y la cultura del pasado. Reino babilónico surgió a principios del segundo milenio antes de Cristo, que ha sustituido a Sumer y Akkad, y existía antes de la conquista de Persia en el 539 aC Escribieron en Babilonia, como todos recordamos, en tablillas de arcilla con escritura cuneiforme usar ese muy bien conservado, a diferencia del papel, papiro, y cosas por el estilo, así que saben mucho y sobre Babilonia, y sobre sus matemáticas. Pero, por supuesto, no lo sabemos todo. A diferencia de los griegos, los babilonios han dejado los algoritmos exactos y clara explicación de sus métodos. Ahora sólo podemos adivinar cómo los babilonios actuar en un caso particular, para resolver el problema. En este trabajo me sosredtochus principalmente en la aritmética babilónica, dejando de lado la geometría, el álgebra y astronomía.
Los babilonios en matemáticas progresado mucho más allá de los egipcios, como la conocemos, pero no alcanzó a los griegos, al parecer. Ellos ya saben cómo resolver ecuaciones de segundo grado, además tenía algunos rudimentos de álgebra numérica. Uno de sus logros fue la introducción de sexagesimal posicional sin un rasguño. Esto significa que el tratamiento con los números a ser mucho más flexible y más simple que en Egipto. Simplemente no sé de dónde vino ese sistema. Una versión dice que ha dado lugar a una mezcla de sistemas de 10-arias de los pueblos de Sumer y Akkad 6-aria y. Pero hay otras ideas sobre este tema.
Este sistema, por desgracia (quizás afortunadamente, no quiero enseñarles las tablas de multiplicar) no era aplicable a otras naciones del mundo antiguo, y tuvo que esperar a la llegada del sistema posicional indio. Sin embargo, lo que refleja las matemáticas babilónicas en nuestra cultura sigue siendo: la división de minutos por hora, sesenta segundos y 60 minutos - un eco del antiguo sistema de numeración babilónica
.
Los números y el
sistema numérico
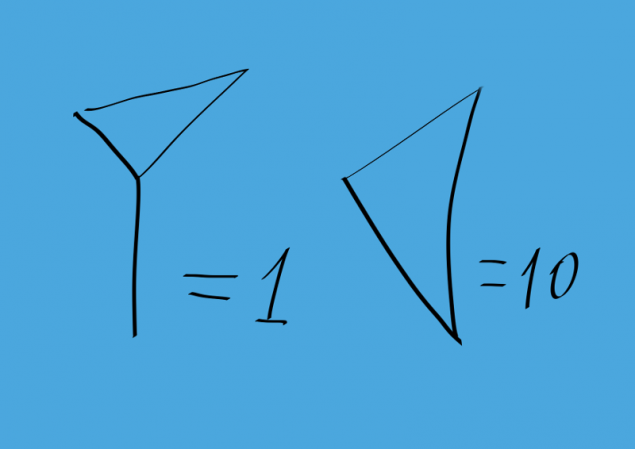
La imagen muestra cómo los babilonios es 1 y 10. Con su ayuda, retrata todos los números del 1 al 59. El cuadro siguiente muestra el número 33. Esto es similar a la romana y otro sistema nonpositional de escribir los números.
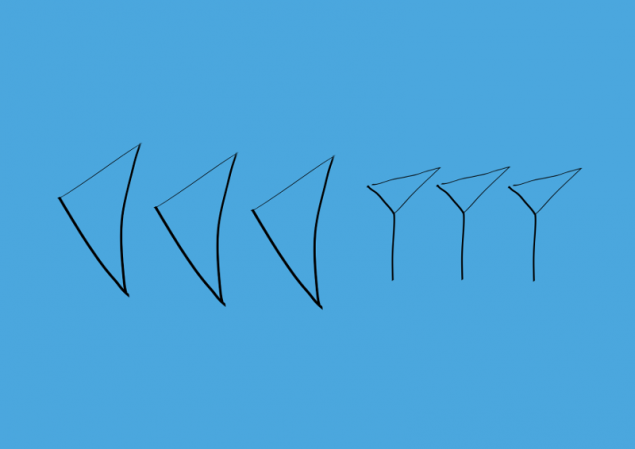
El número 60 expresó exactamente como una unidad. En el principio fue dibujado más grande pero más tarde borró esa distinción. Números mayores que 60 pero menor que 120 se designan como sigue: número 60 escrito primero, y luego a través de la brecha el resto del número, el más pequeño 60.
A continuación se muestra un ejemplo de 63

Los números de la forma K * 60 + n (1 & lt; = K & lt; 60; n = 1, 2, 3, ... 59). I> designado por analogía, como en el ejemplo siguiente
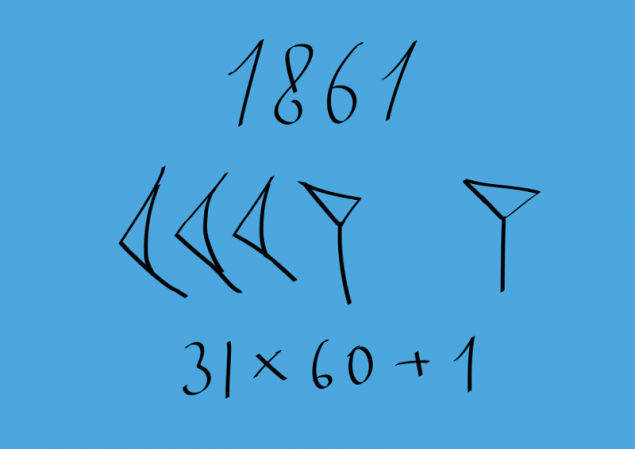
Los babilonios no eran 0, pero con el tiempo se le ocurrió utilizar una señal de lo que significaba trozos faltantes. Esta marca sólo se aplica al número de bits en el interior y no se planteó al final. He aquí un ejemplo en la imagen.
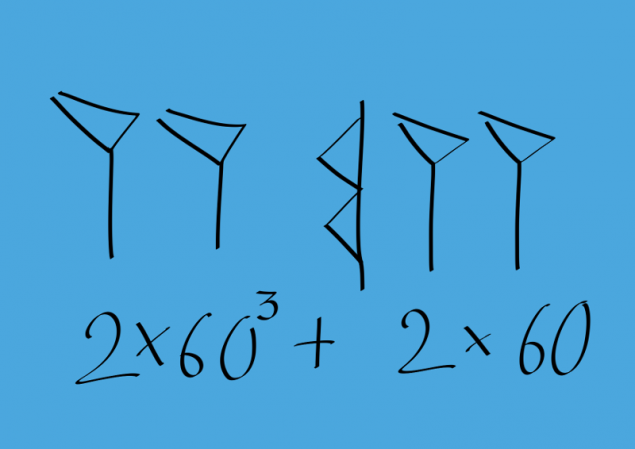
El problema es que este número podría ser leído y como 2 * 60 ^ 2 2, y como 2 * 60 ^ 5 + 2 * 60 ^ 3. Muy incómodo! Este sistema de grabación tendría lugar a numerosos errores, ¿no crees? Los babilonios trataron con mucho cuidado para separar las descargas para evitar confusiones (mucho más ordenado que yo). Sin embargo, en algunos casos, es muy probable que el error. Hay ejemplos de grandes números cuando el número de parte transferida a otra línea. Trate de averiguar aquí, eso significa! Pero el número de errores en los textos babilónicos es pequeña, a pesar de que están allí.
El mismo método fue designada y fracciones. Sólo un muy popular 1/2, 1/3 y 2/3 eran insignias especiales.
Dondequiera que voy a seguir para registrar el número de Babilonia, que separa el punto de descarga y parte entera de la fracción con un punto y coma. Por ejemplo: 177 es 2, 57, etc. Nivel Perdidas, voy a sustituir a 0.
Cálculos
Dado que el sistema era una posición babilonios, sus cálculos eran rchen similar a la nuestra. Cuando la suma y la resta, que acaba de sumar y restar números dígito por dígito. Una ventaja adicional fue que los dígitos sexagesimales indican de manera nonpositional por unidades y decenas, y en tal sistema para restar y añadir mucho más fácil que en nuestra notación abstracta que requiere mesa especial aprender adición.
Multiplicación, como puede imaginar, también, fue similar a la nuestra. Pero ellos usaron su vasta tabla de multiplicar? Enseñaron de memoria? Ellos se prepararon mesas especiales donde se puede ver la obra.
De los babilonios que ha sobrevivido muchas tablas de multiplicar, pero no incluyen todas las obras de números "inequívocas" como decimal nuestra mesa. Su tabla comienza de 1 a 20 inclusive, a continuación, seguido de las obras de 30, 40, 50. Si los babilonios querían multiplicar 35 por 47, que tenía que encontrar una mesa primero 35 * 40, entonces 35 * 7 y doblar. Esto requiere una acción adicional, pero también lo podría ahorrar significativamente el espacio.
División como una acción independiente babilonios no conocían. En su lugar, utilizan la multiplicación por el número inverso. Para ello, por supuesto, que necesitaban los números inversos de mesa. Por ejemplo, si era necesario dividir 1 15 5 1/5 babilónico encontró que sus registros serán nuestro 0; 12 y multiplicar 1, 15 a 0, 12. Si este número no expresa una fracción sexagesimal final, los babilonios buscando un número que multiplicado por el divisor dio dividendos.
Por ejemplo, se divide 22, 45, 0 6, 30. En este caso, tal condición se afirma: "¿Qué tengo que tomar 6, 30 para obtener 22, 45, 0? "La respuesta es 3, 30. Por supuesto, los babilonios utilizaban y valores aproximados cuando sea necesario.
Tablas recíprocos aspecto:
2 30 3 20 < 4 15 5 12 6 10 8 7; 30 9 6; 40 12 5 15 4 16 3; 45 18 3;. 20 20 3 Y así sucesivamente
Además de la tabla de valores inversos, los babilonios tenían muchas otras tablas: cuadrados, cubos, raíces cuadradas y cúbicas, y algunos otros.
Tareas
¿Qué problemas podría resolver los babilonios?
Por ejemplo, como:
"10 hermanos y 1 2/3 enteros y plata minas. Hermano hermano anteriormente. Por lo que es más alto, yo no lo sé. Comparte octavo hermano 6 shekels. Brother en hermano de la cantidad más alta? " I>
El objetivo es dividir la suma entre los hermanos de modo que la proporción de cada componente de una progresión aritmética y para encontrar la diferencia de la progresión.
Por supuesto, los babilonios y resuelve el problema de los intereses. Incluyendo problemas en el interés compuesto:
"Una gur le di al crecimiento. ¿Después de cuántos años va a crecer por sí mismo? " I>
Porcentaje asumió 0; 12 por año. Algunos investigadores han sugerido que los babilonios poseían los inicios de los logaritmos. Otros están en desacuerdo con ellos.
Otro ejemplo incluye ecuaciones cuadráticas:
«La zona de las dos plazas de la pila, y es 37, 5. lateral de la plaza es de 2/3 de otra plaza. 10 más se añadieron además a un lado, al lado de la más pequeña 5 se añadieron además. Estas plazas son eso? » I>
En las tablas, estos problemas son con la explicación de su decisión. Se puede observar que los babilonios conocidos ecuaciones cuadráticas y el sistema de ecuaciones lineales.
¿Los babilonios y raíces cuadradas, que se calcularon utilizando las fórmulas aproximadas:
"Cuadrado Diagonal tiene 10. Encuentra el lado de un cuadrado. 10 a 0, 42, 30 multiplicar el 7, 5, tener una fiesta. 7, 5, 1; 25 a multiplicar. 10 y 25 se da ".
Fuente: geektimes.ru/post/252310/























