1480
So thought the ancients. Babylon
This is a continuation conceived me about the history of the series of calculations and accounts. The first article about Egypt here .
Now I will try to talk a little bit about the other great civilization and culture of the past. Babylonian kingdom emerged at the beginning of the 2nd millennium BC, it has replaced Sumer and Akkad, and existed before the conquest of Persia in 539 BC They wrote in Babylon, as we all remember, on clay tablets with cuneiform using that very well preserved, unlike paper, papyrus, and things like that, so we know quite a lot and about Babylon and about his mathematics. But, of course, we do not know everything. Unlike the Greeks, the Babylonians have left the exact algorithms and clear explanation of its methods. Now we can only guess how the Babylonians act in a particular case to solve the problem. In this paper I sosredtochus primarily on the Babylonian arithmetic, leaving aside the geometry, algebra and astronomy.
The Babylonians in mathematics progressed far beyond the Egyptians, as we know, but not caught up with the Greeks, apparently. They already know how to solve quadratic equations, in addition had some rudiments of numerical algebra. One of their achievements was the introduction of positional sexagesimal without a scratch. This means that the treatment with the numbers become much more flexible and simpler than in Egypt. Just do not know where it came from such a system. One version says that it has resulted in a mixture of 6-ary and 10-ary systems of the peoples of Sumer and Akkad. But there are other ideas on this subject.
This system, unfortunately (perhaps fortunately, do not want to teach them multiplication tables) was not applicable to other nations of the Ancient World, and had to wait for the arrival of the Indian positional system. However, something which reflected Babylonian mathematics in our culture remains: the division of minutes per hour, and sixty seconds to 60 minutes - an echo of the ancient Babylonian number system.
Numbers and the number system
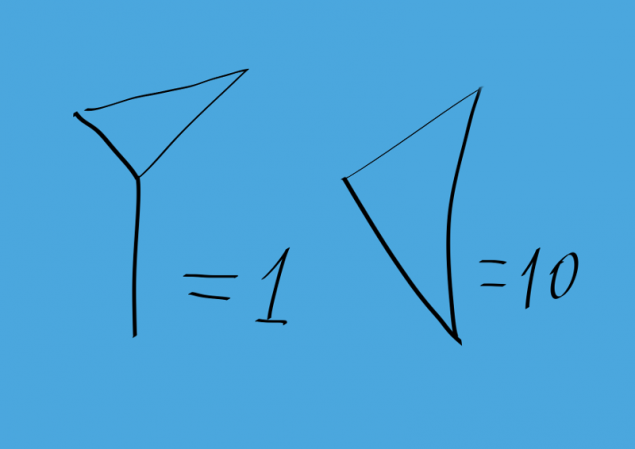
The picture shows how the Babylonians is 1 and 10. With their help, portrayed all the numbers from 1 to 59. The picture below shows the number 33. This is similar to the Roman and other nonpositional system of writing numbers.
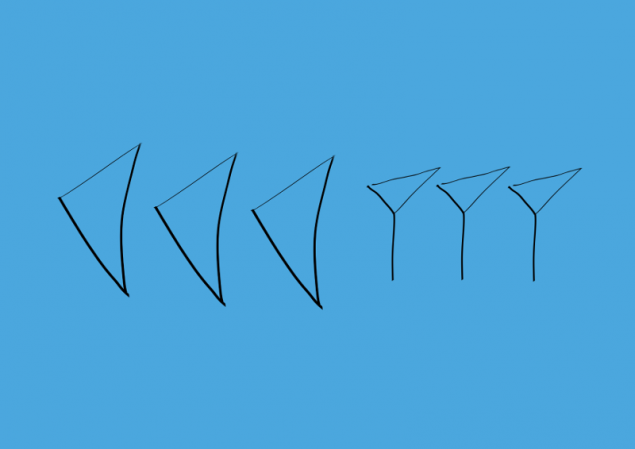
The number 60 expressed exactly as a unit. In the beginning it was drawn larger but later erased that distinction. Numbers greater than 60 but less than 120 are designated as follows: first written number 60, and then through the gap the rest of the number, the smaller 60.
Below is an example of 63

The numbers of the form K * 60 + n (1 & lt; = K & lt; 60; n = 1, 2, 3, ... 59) i> designated by analogy, as in the example below.
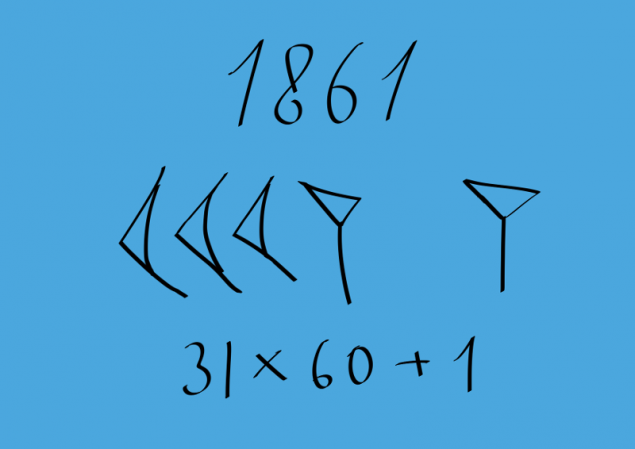
The Babylonians were not 0, but over time they came up with to use a sign which meant missing bits. This mark applies only to the number of bits inside and was not raised at the end. Here is an example in the picture.
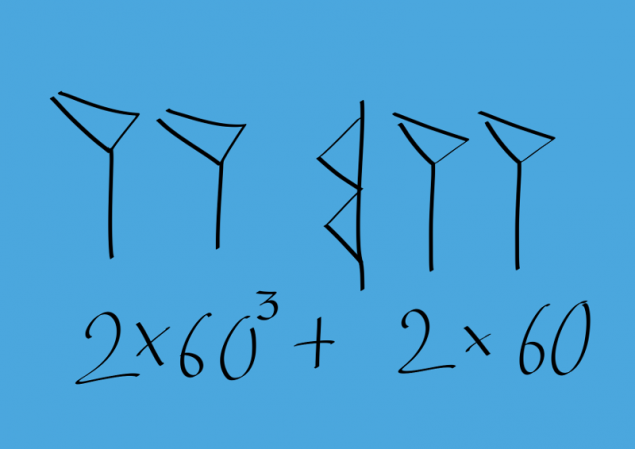
The problem is that this number could be read and as 2 * 60 ^ 2 2, and as 2 * 60 ^ 5 + 2 * 60 ^ 3. Very uncomfortable! This recording system would have lead to numerous errors, do not you think? The Babylonians tried very carefully to separate discharges to avoid confusion (much neater than I). Yet in some cases, the error is very likely. There are examples of large numbers when the part number transferred to another line. Try to figure it out here, that meant! But the number of errors in the Babylonian texts is small, although they are over there.
The same method was designated and fractions. Only a very popular 1/2, 1/3 and 2/3 were special badges.
Everywhere I'm going to continue to record the number of Babylonian, separating discharge point and integer part of the fraction with a semicolon. For example: 177 is 2, 57, etc. Missed level, I will replace 0.
Calculations
Since the system was a positional Babylonians, their calculations were rchen similar to ours. When addition and subtraction, they just add and subtract numbers digit by digit. An additional advantage was that the sexagesimal digits indicate nonpositional manner by ones and tens, and in such a system to subtract and add much easier than in our abstract notation requiring special table learn addition.
Multiplication, as you might guess, too, was similar to ours. But they used their vast multiplication table? They taught it by heart? They were prepared special tables where you can watch the work.
From the Babylonians to have survived many multiplication tables, but they did not include all the works of "unambiguous" numbers as decimal our table. Their table starts from 1 to 20 inclusive, then followed the works of 30, 40, 50. If the Babylonians wanted to multiply 35 by 47, he had to find a table first 35 * 40, then 35 * 7 and fold. This required extra action, but so could significantly save space.
Division as an independent action Babylonians did not know. Instead they used multiplication by the inverse number. To do this, of course, they needed the table inverse numbers. For example, if it was necessary to divide 1 15 5 1/5 the Babylonian found that their records will be our 0; 12 and multiply 1, 15 to 0; 12. If this number does not express a final sexagesimal fraction, the Babylonians were looking for a number that when multiplied by the divisor gave dividend.
For example, you divide 22, 45, 0 6, 30. In this case, such a condition is stated: "What do I need to take 6, 30 to get 22, 45, 0? "The answer is 3, 30. Of course, the Babylonians used and approximate values when needed.
Tables reciprocals look like this:
2 30 3 20 < 4 15 5 12 6 10 8 7; 30 9 6; 40 12 5 15 4 16 3; 45 18 3; 20 20 3 And so on.
In addition to the table of inverse values, the Babylonians had many other tables: squares, cubes, square and cube roots, and some others.
Tasks
What problems could solve the Babylonians?
For example, such:
"10 brothers and 1 2/3 whole and silver mines. Brother brother above. As far as it is higher, I do not know. Share eighth brother 6 shekels. Brother on brother on how much higher? " I>
The goal is to divide the sum between the brothers so that the proportion of each component of an arithmetic progression and to find the difference of the progression.
Of course, the Babylonians and solved the problem of the interest. Including problems on compound interest:
"One gur he gave to the growth. After how many years it will grow by itself? " I>
Percentage assumed 0; 12 per annum. Some researchers have suggested that the Babylonians possessed the beginnings of logarithms. Others disagree with them.
Another example includes quadratic equations:
«The area of the two squares of the pile, and it is 37, 5. Side of the square is 2/3 of another square. 10 more were added besides to the side, to the side of the smaller 5 were added besides. These squares are that? » I>
In the tables, these problems are with the explanation of their decision. It can be seen that the Babylonians known quadratic equations and the system of linear equations.
Did the Babylonians and square roots, which were calculated using approximate formulas:
"Diagonal square has 10. Find the side of a square. 10 to 0, 42, 30 multiply the 7, 5, have a party. 7, 5, 1; 25 to multiply. 10 and 25 it gives ".
Source: geektimes.ru/post/252310/
Now I will try to talk a little bit about the other great civilization and culture of the past. Babylonian kingdom emerged at the beginning of the 2nd millennium BC, it has replaced Sumer and Akkad, and existed before the conquest of Persia in 539 BC They wrote in Babylon, as we all remember, on clay tablets with cuneiform using that very well preserved, unlike paper, papyrus, and things like that, so we know quite a lot and about Babylon and about his mathematics. But, of course, we do not know everything. Unlike the Greeks, the Babylonians have left the exact algorithms and clear explanation of its methods. Now we can only guess how the Babylonians act in a particular case to solve the problem. In this paper I sosredtochus primarily on the Babylonian arithmetic, leaving aside the geometry, algebra and astronomy.
The Babylonians in mathematics progressed far beyond the Egyptians, as we know, but not caught up with the Greeks, apparently. They already know how to solve quadratic equations, in addition had some rudiments of numerical algebra. One of their achievements was the introduction of positional sexagesimal without a scratch. This means that the treatment with the numbers become much more flexible and simpler than in Egypt. Just do not know where it came from such a system. One version says that it has resulted in a mixture of 6-ary and 10-ary systems of the peoples of Sumer and Akkad. But there are other ideas on this subject.
This system, unfortunately (perhaps fortunately, do not want to teach them multiplication tables) was not applicable to other nations of the Ancient World, and had to wait for the arrival of the Indian positional system. However, something which reflected Babylonian mathematics in our culture remains: the division of minutes per hour, and sixty seconds to 60 minutes - an echo of the ancient Babylonian number system.
Numbers and the number system
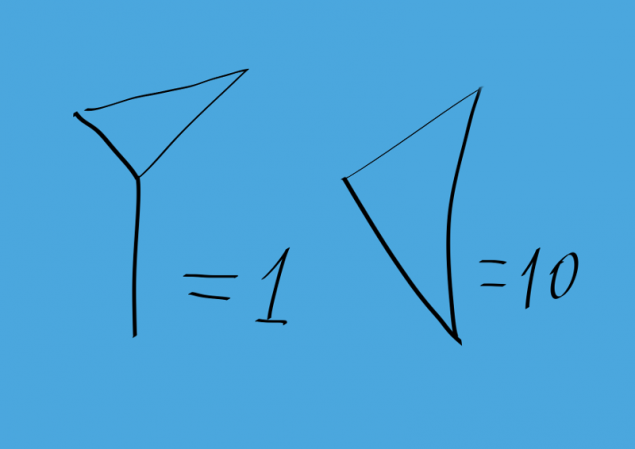
The picture shows how the Babylonians is 1 and 10. With their help, portrayed all the numbers from 1 to 59. The picture below shows the number 33. This is similar to the Roman and other nonpositional system of writing numbers.
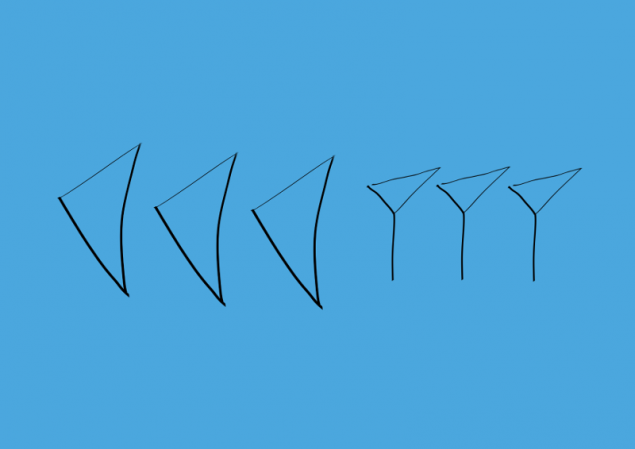
The number 60 expressed exactly as a unit. In the beginning it was drawn larger but later erased that distinction. Numbers greater than 60 but less than 120 are designated as follows: first written number 60, and then through the gap the rest of the number, the smaller 60.
Below is an example of 63

The numbers of the form K * 60 + n (1 & lt; = K & lt; 60; n = 1, 2, 3, ... 59) i> designated by analogy, as in the example below.
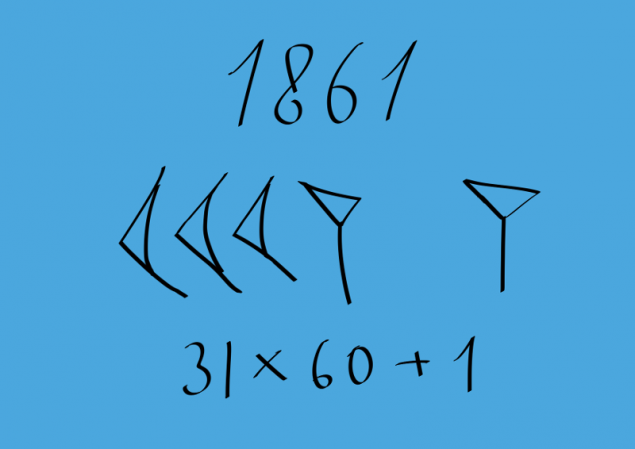
The Babylonians were not 0, but over time they came up with to use a sign which meant missing bits. This mark applies only to the number of bits inside and was not raised at the end. Here is an example in the picture.
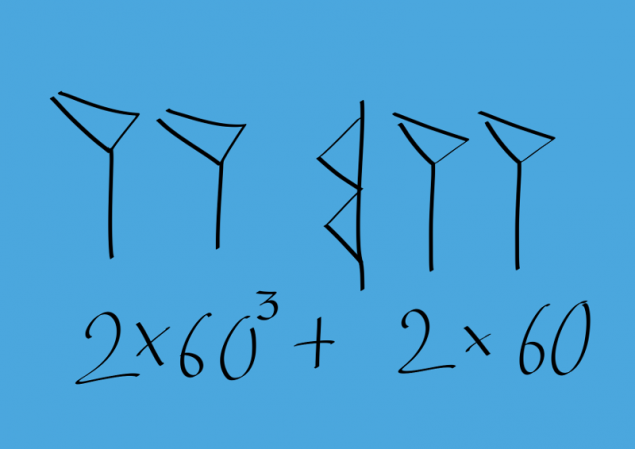
The problem is that this number could be read and as 2 * 60 ^ 2 2, and as 2 * 60 ^ 5 + 2 * 60 ^ 3. Very uncomfortable! This recording system would have lead to numerous errors, do not you think? The Babylonians tried very carefully to separate discharges to avoid confusion (much neater than I). Yet in some cases, the error is very likely. There are examples of large numbers when the part number transferred to another line. Try to figure it out here, that meant! But the number of errors in the Babylonian texts is small, although they are over there.
The same method was designated and fractions. Only a very popular 1/2, 1/3 and 2/3 were special badges.
Everywhere I'm going to continue to record the number of Babylonian, separating discharge point and integer part of the fraction with a semicolon. For example: 177 is 2, 57, etc. Missed level, I will replace 0.
Calculations
Since the system was a positional Babylonians, their calculations were rchen similar to ours. When addition and subtraction, they just add and subtract numbers digit by digit. An additional advantage was that the sexagesimal digits indicate nonpositional manner by ones and tens, and in such a system to subtract and add much easier than in our abstract notation requiring special table learn addition.
Multiplication, as you might guess, too, was similar to ours. But they used their vast multiplication table? They taught it by heart? They were prepared special tables where you can watch the work.
From the Babylonians to have survived many multiplication tables, but they did not include all the works of "unambiguous" numbers as decimal our table. Their table starts from 1 to 20 inclusive, then followed the works of 30, 40, 50. If the Babylonians wanted to multiply 35 by 47, he had to find a table first 35 * 40, then 35 * 7 and fold. This required extra action, but so could significantly save space.
Division as an independent action Babylonians did not know. Instead they used multiplication by the inverse number. To do this, of course, they needed the table inverse numbers. For example, if it was necessary to divide 1 15 5 1/5 the Babylonian found that their records will be our 0; 12 and multiply 1, 15 to 0; 12. If this number does not express a final sexagesimal fraction, the Babylonians were looking for a number that when multiplied by the divisor gave dividend.
For example, you divide 22, 45, 0 6, 30. In this case, such a condition is stated: "What do I need to take 6, 30 to get 22, 45, 0? "The answer is 3, 30. Of course, the Babylonians used and approximate values when needed.
Tables reciprocals look like this:
2 30 3 20 < 4 15 5 12 6 10 8 7; 30 9 6; 40 12 5 15 4 16 3; 45 18 3; 20 20 3 And so on.
In addition to the table of inverse values, the Babylonians had many other tables: squares, cubes, square and cube roots, and some others.
Tasks
What problems could solve the Babylonians?
For example, such:
"10 brothers and 1 2/3 whole and silver mines. Brother brother above. As far as it is higher, I do not know. Share eighth brother 6 shekels. Brother on brother on how much higher? " I>
The goal is to divide the sum between the brothers so that the proportion of each component of an arithmetic progression and to find the difference of the progression.
Of course, the Babylonians and solved the problem of the interest. Including problems on compound interest:
"One gur he gave to the growth. After how many years it will grow by itself? " I>
Percentage assumed 0; 12 per annum. Some researchers have suggested that the Babylonians possessed the beginnings of logarithms. Others disagree with them.
Another example includes quadratic equations:
«The area of the two squares of the pile, and it is 37, 5. Side of the square is 2/3 of another square. 10 more were added besides to the side, to the side of the smaller 5 were added besides. These squares are that? » I>
In the tables, these problems are with the explanation of their decision. It can be seen that the Babylonians known quadratic equations and the system of linear equations.
Did the Babylonians and square roots, which were calculated using approximate formulas:
"Diagonal square has 10. Find the side of a square. 10 to 0, 42, 30 multiply the 7, 5, have a party. 7, 5, 1; 25 to multiply. 10 and 25 it gives ".
Source: geektimes.ru/post/252310/























