The task of the 165-year-old is haunted mathematicians

In 1850 the Rev. Thomas Kirkman, the British mathematician and rector of the parish in Lancashire, has formulated an innocent-looking puzzle in the entertainment magazine for lovers of mathematics "Notebook ladies and gentlemen»:

"Fifteen young schoolgirls go for a walk for seven days in rows of three: you need each day to place them so that the same pair of schoolgirls never met twice in a row».

The task looks simple, but if you try to solve it, you immediately realize that this is not so. You can try to solve it with pencil and paper or play HTML-версию.

Because of its simplicity false problem quickly became famous. His decision sent lovers of mathematics, and scientists have published research papers in an attempt to formulate a common solution to the problem.

As a result, this puzzle has helped to form a new branch of mathematics: combinatorial circuit , who is now dedicated to толстые textbooks . What started as a simple task for distribution to groups of people (or schemes as a result they were called), has now become the method that is used in the experimental design, error correction codes in computer science, cryptography, agriculture, sports, and even fraud gambling (the story was when the criminal cartel has earned millions of dollars in seven years, buying tickets with all possible combinations of 5 out of 46 in the lottery 6 out of 46 if the ticket price was lower than the additional bonuses for winning 5 out of 46, plus the probability of winning the jackpot.) < br />
For example, the classical Hamming code for error correction uses a solution of the problem about the schoolgirls (create groups of three schoolgirls, where no pair of non-recurring), but only to the scheme of the seven girls (bits).



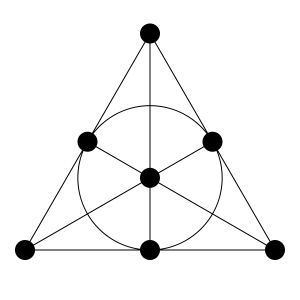
The plane Fano (7, 3, 2) i>

Most amazing of all, that in the 165 years of mathematics have not been able to solve the problem in a general way. They still can not answer, what is the solution in the puzzle for the initial conditions: there are n i> schoolgirls need to create a group size of k i>, so that the set of t i> the girls had never met twice in the same group. This formulation is called scheme (n, k, t) i>.

For example, for a group of 19 women has more than 11 billion possible triplets in which each pair is found only once. This number is the answer. But the number of options is growing exponentially as the number of schoolgirls.

It is clear that the problem is solved under certain conditions and can not be solved in some other. For example, if six write schoolgirls triplets of all the possible pairs, the obvious problem is not solved (co schoolgirl Anna, there are five possible pairs, at the same time in each triplet has two pairs with Anna, but five is not divided by two). That is the principle of divisibility immediately screened out many options (n, k, t) i>.

At the same time, there are (n, k, t) i>, which are consistent with the principle of divisibility, but still have no solution: for example, (47, 3, 2) i>.

Over the past years, the decision became known to many combinations (n, k, t) i>, which have been verified algebraically or enumeration on computers. But how to solve this in a general way what to do with exceptions such as (47, 3, 2) i>? How to understand, it is the task of the decision or not?

This problem has long been considered one of the most famous problems in combinatorics, говорит mathematician Gil Kalai (Gil Kalai) of the Hebrew University in Jerusalem, in an interview with Wired. He remembers arguing about this with colleagues and a half years ago, and they came to the conclusion that "we will never know the answer, because the problem is clearly too complicated».

However, just two weeks the young professor of mathematics Peter Kivash (Peter Keevash) from Oxford showed that Kalai wrong. The scientific article from January 2014, he argues that the solution is almost always there, if the condition of divisibility. The new job from April 2015, he showed how to calculate the approximate number of solutions for the given parameters.

No one expected that to solve the problem, you can apply the theory of probability, but the method has worked perfectly.

Returning to the lottery, the fraudsters have realized that it is possible to reduce the number of tickets purchased, if buy up all the combinations of 5 out of 46 (if you specify 6 of 46 numbers), they will receive additional prizes everything, but can still get the jackpot. Although the scheme (46, 6, 5) i> is not calculated, but there are schemes that are sufficiently close for practical application. One of them is likely to have used a criminal cartel.

The number of new schemes designed constantly growing. Many of them find practical application as (7, 3, 2) i> and (46, 6, 5) i>. Come 1000 page directories with the schemes. However, mathematics is still speculated as to determine whether there is a solution for a specific set of conditions. Thanks Kivashu we learned that the probability of this is quite high. So at least now it is clear that for all the unknowns look better solution than to abandon it. Moreover, there are tools to generate the approximate i> schemes for any parameters.

But thanks to the work Kivasha have hope that we can develop a method to create a exact i> schemes for all parameters. If that happens, it will be an extraordinary breakthrough in mathematics.

However, work is purely theoretical Kivasha. Experts say that the creation of practical mechanisms on the basis of his method will require more hard work of several generations of mathematicians.

Source: geektimes.ru/post/252308/