165-річної задачі супроводжуючих математиків.

У 1850 р. Роверенд Томас Кіркман, британський математик і парафіясний аббот в Ланкаширі, сформульовано невинно-розмальову головоломку в розважальному журналі для любителів математики, Ноутбук Ladies і Gentlemen:

П'ятнадцять молодих школярів вирушають на прогулянку на сім днів поспіль три: слід влаштувати їх щодня, щоб ті ж пара школярів ніколи не зустрілися двічі в одному ряду.

Проблема виглядає просто, але якщо ви намагаєтеся вирішити її, ви відразу розумієте, що це не так. Ви можете спробувати вирішити його олівцем і папером або грати в HTML-версію.

Завдяки своїй помилковій простоті завдання швидко стало відомою. Математологи надсилали свої рішення, а вчені опублікували наукові статті, які намагаються формувати загальне рішення проблеми.

В результаті цього головоломка допомогла формувати нове відділення математики: розчісникальні щілини, до яких зараз присвячуються товсті підручники. Що почалася як проста проблема групування людей (або схем, як вони були в кінцевому підсумку названі) тепер стала методом, який використовується в експериментальному дизайні, корекції помилок в комп'ютерній наукі, криптографії, сільському господарстві, спорту і навіть азартних іграх (відповіли, де кримінальний картель зробив мільйони доларів за сім років, купуючи квитки з усіма можливими 5-ти-46 комбінацій в лотерею 6-of-46, якщо вартість квитків була менша, ніж додаткові бонуси за виграш 5-of-46 плюс ймовірність виграшу джекпоту).

Наприклад, класичний код Hamming використовує проблему школярки для виправлення помилок (підготовки груп трьох школярок, де немає пари повторюється), але тільки для семи-дівочої схеми (bit).



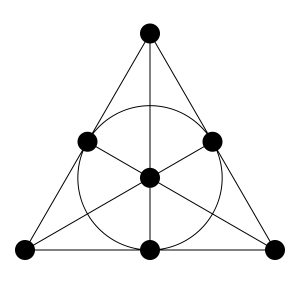
Патерн Фано для (7, 3, 2)

Найдивовижніше, що в 165 років, математики не змогли вирішити проблему взагалі. Вони не можуть сказати вам, що рішення для головоломки на початку: є не школярки, ви повинні створити групи розмірів k, так що набори дівчаток ніколи не зустрічалися двічі в одній групі. Ця формула називається схемою (n, k, t).

Наприклад, для групи 19 дівчат, є більш ніж 11 мільярдів можливих походів, в яких кожна пара відповідає лише один раз. Що таке відповідь. Але кількість варіантів виростає доцільно як кількість школярів зростає.

Зрозуміло, що проблема вирішується в деяких умовах і не вирішується в деяких інших умовах. Наприклад, якщо шість школярів роблять трилетки з усіх можливих пар, проблема явно не вирішується (з школяркою Anya є п'ять можливих пар, одночасно в кожному потрійку є дві пари з Anya, і п'ять не діляться на два). Саме за принципом дивісності відразу ліквідуються безліч варіантів (n, k, t).

У той же час є (n, k, т) які цілком відповідають принципу дивізенціальності, але ще не мають розчину: наприклад (47, 3, 2).

З роками розчин був відомий багатьма поєднаннями (n, k, t), які були випробувані алгебрично або бруте міцно на комп'ютерах. Але як вирішити це в загальних умовах, що робити з винятками типу (47, 3, 2)? Як дізнатися, чи має проблема?

Ця проблема давно була розглянута однією з найвідоміших проблем в combinatorics, говорить математика Гіл Калаї івритського університету в Єрусалимі в інтерв'ю з Wired. Він згадує про це колегами на рік і навпіл тому, і вони уклали, що «ми ніколи не знаємо відповідь, бо завдання явно занадто важко».

Але всього за два тижні пізніше Петро Кеваш, молодший викладач математики від Оксфорда, зарекомендував Калефа неправильно. У січні 2014 року він стверджує, що рішення проблеми практично завжди існує, якщо зустрінеться умова. У новому папері з квітня 2015 року він показав, як розрахувати приблизну кількість розчинів для заданих параметрів.

Не один очікуваний теорія ймовірності наноситься на проблему, але він добре працював.

Повернувшись до лотерей, шахраї зрозуміли, що ви можете зменшити кількість квитків, придбаних якщо ви купуєте всі комбінації 5 з 46 (якщо ви вказали 6 з 46 номерів), то вони отримають абсолютно всі додаткові призи, а також можуть отримати джекпот. Хоча схема (46, 6, 5) ще не обчислюється, є схеми досить близько для практичного застосування. Одна з них, ймовірно, використовувала кримінальний картель.

Кількість нових розрахункових схем постійно зростає. Багато з них знаходять практичні додатки, такі як (7, 3, 2) і (46, 6, 5). Є 1000 сторінок з діаграмами. Тим не менш, математики все ще плутають, як визначити, чи є розчин для конкретного вказаного стану. Завдяки Kivash ми дізналися, що ймовірність цього досить висока. Так, принаймні зараз зрозуміло, що з усіма невідомими, краще шукати рішення, ніж відмовитися від неї. Крім того, є інструменти для створення зразкових схем для будь-яких параметрів.

Але завдяки роботі Kivash було сподіватися, що метод може бути розроблений для створення чітких діаграм для будь-яких параметрів. Якщо це сталося, це буде неординарний прорив у математики.

Тим не менш, робота Ківаша – теоретична. Експерти говорять про те, що створення практичних алгоритмів на основі його методу вимагатиме важкої роботи декількох поколінь математиків.

Джерело: geektimes.ru/post/252308/