805
En la diagonal del cuadrado
La introducción de los números complejos no fue la primera revolución en la comprensión de los números de la naturaleza humana. Durante dos mil años antes de este poderoso golpe para experimentar el mundo de las matemáticas griegas.
Los problemas comenzaron los pitagóricos no lo hicieron inmediatamente. Pitágoras fundó una escuela científica eventualmente terminó mal, pero hoy la historia no es tan alegre masacre que se cometió durante los pitagóricos agradecido por la educación del pueblo, y un mayor grado de giros espirituales y vueltas.
El término "escuela científica" en relación con una organización fundada por Pitágoras, es un eufemismo tal. Sensatamente mirando su estructura y tecnología aplicada, el pitagorismo atribuirse con seguridad a los cultos totalitarios, que era muy en el espíritu de la época (sin embargo, es siempre en el espíritu de la época, clásicos atemporales). Estar presente y el grado de separación de iniciación, y un complejo sistema de rituales con restricciones (por ejemplo, bien conocida, como "no tienen frijoles" o "no morder de todo el pan"), y la doctrina filosófica compleja. Hola compañeros Ron Hubbard. Nada nuevo bajo el sol.
En general, durante la vida de Pitágoras su "escuela" era sólido ahora, además de tener una importante influencia política y en constante crecimiento.
En general, la filosofía de Pitágoras tenía un impacto significativo en la cultura occidental (ya nosotros también). Muchas ideas se han desarrollado en la filosofía griega clásica, y ya conocen el teorema de Pitágoras acerca de todo. La expresión "armonía de las esferas", por cierto, también se remonta a los pitagóricos.
Uno de los elementos esenciales de su filosofía era la idea de que cualquier número puede ser representado como una relación de dos números enteros, que es una fracción simple. En esto, incluyendo la naturaleza de la sierra de la perfección. Por otra parte, parece ser bastante obvio. En matemáticas modernas tales números se llaman racional, y su conjunto se denota por el símbolo . Hacer ahora una pausa durante unos segundos, pensar en donde todos deben ser, eso no es cierto? ¿Puede dar un argumento que sería lo suficientemente convincente para los antiguos griegos? O, al menos, lo suficientemente convincente para mí, en lo personal?
En general, el mundo de los números era simple, elegante, y todo el mundo estaba contento. El origen del problema apareció de forma inesperada, ya se ha convertido en el teorema anterior, que lleva el nombre de Pitágoras, uno de los existentes más importante, sus logros. Desafortunadamente, la prueba de la pitagórica no sabemos. La más antigua que existe - se da en los "Elementos" de Euclides y de fecha 3. BC Permítanme recordarles, el propio Pitágoras vivió en el siglo sexto. BC
Un fragmento del Número Vaticano Manuscrito 190, de fecha 10. BC (Completamente здесь):
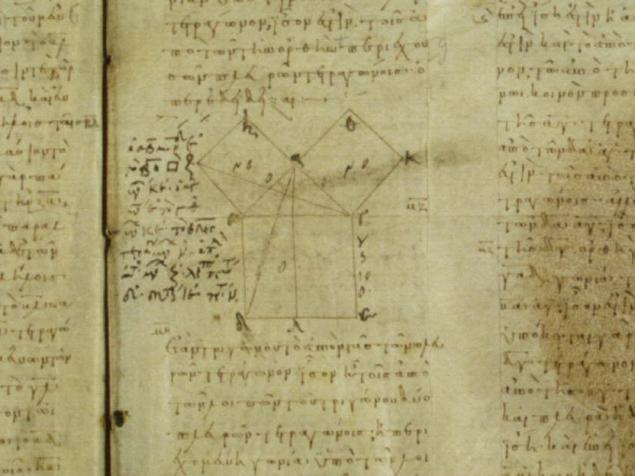
La prueba de Euclides no es un trabajo fácil. Hay razones para creer que él conocía el camino y más fácil, pero debido a consideraciones metodológicas llevó esta opción, mostrando, además del teorema de Pitágoras, y algunas otras ideas interesantes.
Sin embargo, de nuevo a los pitagóricos.
Imagínense una cosa simple: un cuadrado con lados de longitud. Si denotamos la longitud de la diagonal, el teorema de Pitágoras se obtiene:
y, en consecuencia:
Es algo por sí mismo no es un problema. Desde el punto de vista de los pitagóricos, que tendremos que encontrar los números enteros y de tal manera que
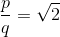
Aquí en este tipo de punto y todo lo "simple" se detuvieron. Y apretado. Esto duró hasta el tope, hasta que un hombre sabio (supuestamente Hípaso también Pitágoras), no demostró, de repente, que no existen estos números. Todo el mal viene de una porción del helluva de listo, como usted sabe. Según la leyenda, este logro científico colegas tan sorprendido de que, con motivo del reconocimiento del mérito científico, sin demora Hípaso arrojado por la borda, y en ese momento él estaba en sus conocimientos matemáticos navegado. Pero no había nada para estropear personas respetadas, socavar los cimientos tan amorosamente nutrido y sistema altamente rentable de la filosofía.
Ahora, el número no se representa como una relación de dos números enteros, llamado irracional.
En algún momento incluso los pitagóricos mantuvo en secreto el hecho de irracionalidad. Sin embargo, el asesinato saldrá a la luz, y la verdad es bastante rápido (en términos históricos) ha encontrado una salida.
Demostrar la irracionalidad no es difícil.
Supongamos que existen tales que
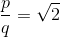
Por otra parte, se supone que al menos uno de los números - impar. Si este no es el caso, el numerador y el denominador siempre se pueden reducir en un 2 (la cantidad adecuada de tiempo).
Luego obtenemos:
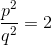
aquí:
Por lo tanto, - un número par. Pero entonces - incluso
.
Por hipótesis, la rareza de al menos uno de los números, encontramos que -. Extraño
Por la paridad puede ser escrito
,
donde - en su conjunto
. Pero entonces:
de ahí
Pero esto significa que - incluso, y aún así. Contradicción.
El número de imposible i> representada como una relación de dos números enteros.
Queda por añadir que - esto no es un extraño fenómeno. Se puede demostrar que los números más irracionales que racionales, más fundamentalmente. Por cierto, la relación es mayor que, menor que en el mundo de los conjuntos infinitos sí es muy kontrituitivnym. Pero eso es otra historia.
PS. Aprovecho esta oportunidad para felicitar a habrovchan llegando. Buena suerte en el nuevo año!
Fuente: habrahabr.ru/post/246963/
Los problemas comenzaron los pitagóricos no lo hicieron inmediatamente. Pitágoras fundó una escuela científica eventualmente terminó mal, pero hoy la historia no es tan alegre masacre que se cometió durante los pitagóricos agradecido por la educación del pueblo, y un mayor grado de giros espirituales y vueltas.
El término "escuela científica" en relación con una organización fundada por Pitágoras, es un eufemismo tal. Sensatamente mirando su estructura y tecnología aplicada, el pitagorismo atribuirse con seguridad a los cultos totalitarios, que era muy en el espíritu de la época (sin embargo, es siempre en el espíritu de la época, clásicos atemporales). Estar presente y el grado de separación de iniciación, y un complejo sistema de rituales con restricciones (por ejemplo, bien conocida, como "no tienen frijoles" o "no morder de todo el pan"), y la doctrina filosófica compleja. Hola compañeros Ron Hubbard. Nada nuevo bajo el sol.
En general, durante la vida de Pitágoras su "escuela" era sólido ahora, además de tener una importante influencia política y en constante crecimiento.
En general, la filosofía de Pitágoras tenía un impacto significativo en la cultura occidental (ya nosotros también). Muchas ideas se han desarrollado en la filosofía griega clásica, y ya conocen el teorema de Pitágoras acerca de todo. La expresión "armonía de las esferas", por cierto, también se remonta a los pitagóricos.
Uno de los elementos esenciales de su filosofía era la idea de que cualquier número puede ser representado como una relación de dos números enteros, que es una fracción simple. En esto, incluyendo la naturaleza de la sierra de la perfección. Por otra parte, parece ser bastante obvio. En matemáticas modernas tales números se llaman racional, y su conjunto se denota por el símbolo . Hacer ahora una pausa durante unos segundos, pensar en donde todos deben ser, eso no es cierto? ¿Puede dar un argumento que sería lo suficientemente convincente para los antiguos griegos? O, al menos, lo suficientemente convincente para mí, en lo personal?
En general, el mundo de los números era simple, elegante, y todo el mundo estaba contento. El origen del problema apareció de forma inesperada, ya se ha convertido en el teorema anterior, que lleva el nombre de Pitágoras, uno de los existentes más importante, sus logros. Desafortunadamente, la prueba de la pitagórica no sabemos. La más antigua que existe - se da en los "Elementos" de Euclides y de fecha 3. BC Permítanme recordarles, el propio Pitágoras vivió en el siglo sexto. BC
Un fragmento del Número Vaticano Manuscrito 190, de fecha 10. BC (Completamente здесь):

La prueba de Euclides no es un trabajo fácil. Hay razones para creer que él conocía el camino y más fácil, pero debido a consideraciones metodológicas llevó esta opción, mostrando, además del teorema de Pitágoras, y algunas otras ideas interesantes.
Sin embargo, de nuevo a los pitagóricos.
Imagínense una cosa simple: un cuadrado con lados de longitud. Si denotamos la longitud de la diagonal, el teorema de Pitágoras se obtiene:
y, en consecuencia:
Es algo por sí mismo no es un problema. Desde el punto de vista de los pitagóricos, que tendremos que encontrar los números enteros y de tal manera que
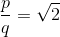
Aquí en este tipo de punto y todo lo "simple" se detuvieron. Y apretado. Esto duró hasta el tope, hasta que un hombre sabio (supuestamente Hípaso también Pitágoras), no demostró, de repente, que no existen estos números. Todo el mal viene de una porción del helluva de listo, como usted sabe. Según la leyenda, este logro científico colegas tan sorprendido de que, con motivo del reconocimiento del mérito científico, sin demora Hípaso arrojado por la borda, y en ese momento él estaba en sus conocimientos matemáticos navegado. Pero no había nada para estropear personas respetadas, socavar los cimientos tan amorosamente nutrido y sistema altamente rentable de la filosofía.
Ahora, el número no se representa como una relación de dos números enteros, llamado irracional.
En algún momento incluso los pitagóricos mantuvo en secreto el hecho de irracionalidad. Sin embargo, el asesinato saldrá a la luz, y la verdad es bastante rápido (en términos históricos) ha encontrado una salida.
Demostrar la irracionalidad no es difícil.
Supongamos que existen tales que
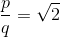
Por otra parte, se supone que al menos uno de los números - impar. Si este no es el caso, el numerador y el denominador siempre se pueden reducir en un 2 (la cantidad adecuada de tiempo).
Luego obtenemos:
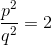
aquí:
Por lo tanto, - un número par. Pero entonces - incluso
.
Por hipótesis, la rareza de al menos uno de los números, encontramos que -. Extraño
Por la paridad puede ser escrito
,
donde - en su conjunto
. Pero entonces:
de ahí
Pero esto significa que - incluso, y aún así. Contradicción.
El número de imposible i> representada como una relación de dos números enteros.
Queda por añadir que - esto no es un extraño fenómeno. Se puede demostrar que los números más irracionales que racionales, más fundamentalmente. Por cierto, la relación es mayor que, menor que en el mundo de los conjuntos infinitos sí es muy kontrituitivnym. Pero eso es otra historia.
PS. Aprovecho esta oportunidad para felicitar a habrovchan llegando. Buena suerte en el nuevo año!
Fuente: habrahabr.ru/post/246963/
Las barreras térmicas, lápidas y otras delicias de placas de circuito impreso
Cuando la tecnología necesita por delante: la forma de pensar en el desarrollo de las TI en 1985