806
Про нас
Введення складних чисел не було першої революції в людському розумінні природи кількості. Два тисячі років раніше, світ давньогрецької математики пережили потужний удар.
Помилки П'ятогогореані не починаються відразу. Наукова школа, заснована Питгорою, закінчилася погано, але сьогодні історія не про життєздатний погром, який був здійснений проти Питогоги за допомогою людей, вдячних за їх освітлення, але більше про духовні івічності.
Термін «наукова школа» в довідці на організацію, засноване Питагорасом, є своєрідним еупемізмом. У своїй структурі та застосованих технологіях, Питагореанізм повинен бути безпечно приписаний до загальної культури, яка була досить в дусі часу (як правило, це завжди в дусі часу, вічної класики). На рівні ініціації, і комплексна система обрядів з заборонами (наприклад, відомі, як «не з'їсти квасолю» або «не вкусити весь бункер), а комплексна філософська доктрина. Гей, співак Ron Hubbard. Ніщо новий під місяць.
В цілому, під час життя Питгори, його «школа» був твердим підприємством, крім значних і постійно зростаючих політичних впливів.
В цілому філософія Питагораса мала значний вплив на західну культуру (в тому числі на нас). Багато ідей знайшли свій розвиток в класичному грецькому філософії, і кожен знає про теорему Питгора. Висловлення «гармонія сфер», до речі, також йде назад до П'ятогогореана.
Одна з основних елементів їх філософії була ідея, що будь-який номер може бути представлений як співвідношення двох цілих, тобто як просту дробу. У цьому, вони побачили досконалість природи кількості. До того ж, здавалося б, цілком зрозуміло. У сучасній математики такі цифри називають раціональними, а їх набір позначається знаком. Тепер про те, де вона виходить? Чи можете ви зробити аргумент, який буде переконливо для давньогрецької? Або хоча б переконливо для себе?
В цілому світ номерів був простий, елегантний, і кожен був щасливий. Джерело неприємностей, раптово, вже згадувалося про те, що ім'я П'ятагораса: одна з найважливіших, відчуттів, його досягнення. На жаль, доказ того, що Pythagoras не знає. Стародавній екстант дається в елементах Euclid і датується 3 ст. до н.е. Нагадуємо, що Пітагорас проживав у 6 столітті. й
Фрагмент від Vatican Manuscript Кількість 190, знайомства з 10-го століття AD (див. тут):
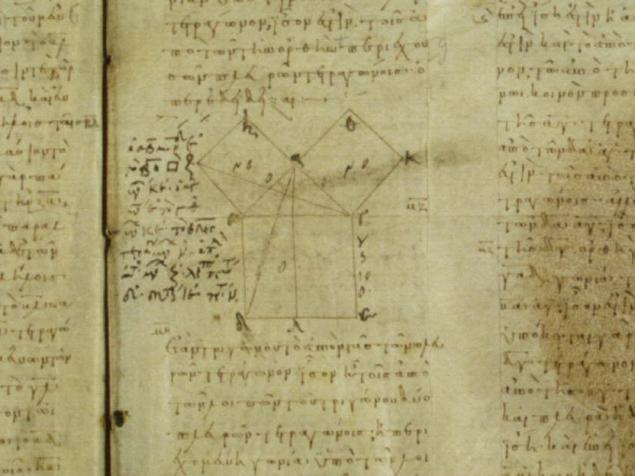
Вистоювання Euclid далеко від найпростішого. Звісно, що він знає спосіб і простіше, але для методологічних причин він дав цю версію, демонструючи, крім самої теореми Питгора, і деякі інші цікаві ідеї.
Але повернувшись до Питагореана.
Так уявіть найпростішу річ: квадрат з однотонними сторонами. Якщо ми позначаємо довжину своєї діагоналі, то згідно з теоремою Питагореана ми отримуємо:
і відповідно:
Не проблема в собі. З точки зору Pythagoreans, потрібно було лише знайти цілі і,
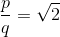
Саме в цьому «прості» момент, що все закладено. І щільно. У той же час, коли продовжив мудрий чоловік (Хіппи Metapontus, також Pythagorean) раптом зарекомендували, що такі цифри не існують. Все зло виходить з дуже розумного, як ви знаєте. Згідно з легендою, це наукове досягнення шокованих колег так багато, що в визнання наукового подвір'я, Хіппа було швидко кинутися над судном, на якому він в момент його математичного розуміння був плаваючий. Але не було нічого не зіпсувати поважних людей, щоб підірвати основи такої словінгово ненав'язливої і дуже прибуткової філософської системи.
Тепер номери, які не містяться у зв'язку з двома цілостями, називаються ірраціональними номерами.
За деякий час Пітагореани навіть зберігали факт порушення секрету. Однак пошиття в сумці не може сховатися, і правда досить швидко (за історичними стандартами) знайшли вихід.
Випробування ірраціональності не складно.
Нехай є ті, хто
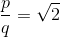
Більш того, нехай ми припустимо, що принаймні одна з чисел непарна. Якщо це не справа, то нумер і деномінатор дроби завжди можна зменшити на 2 (потрібна кількість разів).
Далі ми отримуємо:
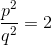
звідси:
Так це навіть число. А потім це навіть.
За умови непарності принаймні одного з чисел ми отримуємо це - непарно.
За рахунок парності можна писати
й
де є ціле.
А потім:
Головна
Але це означає, що він навіть, і тому навіть. Контрадикція.
Номер не може бути представлений як співвідношення двох цілих чисел.
Залишилося додавати, що це не дивно. Це може бути показано, що є більш раціональні числа, ніж раціональні. До речі, більш-менше співвідношення в світі нескінченних наборів є дуже протитуційним. Але це ще одна історія.
ПС. Я приймаю цю можливість привітати Хабровітів на наступ. Успіхів у новому році!
Джерело: habrahabr.ru/post/246963/
Помилки П'ятогогореані не починаються відразу. Наукова школа, заснована Питгорою, закінчилася погано, але сьогодні історія не про життєздатний погром, який був здійснений проти Питогоги за допомогою людей, вдячних за їх освітлення, але більше про духовні івічності.
Термін «наукова школа» в довідці на організацію, засноване Питагорасом, є своєрідним еупемізмом. У своїй структурі та застосованих технологіях, Питагореанізм повинен бути безпечно приписаний до загальної культури, яка була досить в дусі часу (як правило, це завжди в дусі часу, вічної класики). На рівні ініціації, і комплексна система обрядів з заборонами (наприклад, відомі, як «не з'їсти квасолю» або «не вкусити весь бункер), а комплексна філософська доктрина. Гей, співак Ron Hubbard. Ніщо новий під місяць.
В цілому, під час життя Питгори, його «школа» був твердим підприємством, крім значних і постійно зростаючих політичних впливів.
В цілому філософія Питагораса мала значний вплив на західну культуру (в тому числі на нас). Багато ідей знайшли свій розвиток в класичному грецькому філософії, і кожен знає про теорему Питгора. Висловлення «гармонія сфер», до речі, також йде назад до П'ятогогореана.
Одна з основних елементів їх філософії була ідея, що будь-який номер може бути представлений як співвідношення двох цілих, тобто як просту дробу. У цьому, вони побачили досконалість природи кількості. До того ж, здавалося б, цілком зрозуміло. У сучасній математики такі цифри називають раціональними, а їх набір позначається знаком. Тепер про те, де вона виходить? Чи можете ви зробити аргумент, який буде переконливо для давньогрецької? Або хоча б переконливо для себе?
В цілому світ номерів був простий, елегантний, і кожен був щасливий. Джерело неприємностей, раптово, вже згадувалося про те, що ім'я П'ятагораса: одна з найважливіших, відчуттів, його досягнення. На жаль, доказ того, що Pythagoras не знає. Стародавній екстант дається в елементах Euclid і датується 3 ст. до н.е. Нагадуємо, що Пітагорас проживав у 6 столітті. й
Фрагмент від Vatican Manuscript Кількість 190, знайомства з 10-го століття AD (див. тут):

Вистоювання Euclid далеко від найпростішого. Звісно, що він знає спосіб і простіше, але для методологічних причин він дав цю версію, демонструючи, крім самої теореми Питгора, і деякі інші цікаві ідеї.
Але повернувшись до Питагореана.
Так уявіть найпростішу річ: квадрат з однотонними сторонами. Якщо ми позначаємо довжину своєї діагоналі, то згідно з теоремою Питагореана ми отримуємо:
і відповідно:
Не проблема в собі. З точки зору Pythagoreans, потрібно було лише знайти цілі і,
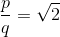
Саме в цьому «прості» момент, що все закладено. І щільно. У той же час, коли продовжив мудрий чоловік (Хіппи Metapontus, також Pythagorean) раптом зарекомендували, що такі цифри не існують. Все зло виходить з дуже розумного, як ви знаєте. Згідно з легендою, це наукове досягнення шокованих колег так багато, що в визнання наукового подвір'я, Хіппа було швидко кинутися над судном, на якому він в момент його математичного розуміння був плаваючий. Але не було нічого не зіпсувати поважних людей, щоб підірвати основи такої словінгово ненав'язливої і дуже прибуткової філософської системи.
Тепер номери, які не містяться у зв'язку з двома цілостями, називаються ірраціональними номерами.
За деякий час Пітагореани навіть зберігали факт порушення секрету. Однак пошиття в сумці не може сховатися, і правда досить швидко (за історичними стандартами) знайшли вихід.
Випробування ірраціональності не складно.
Нехай є ті, хто
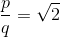
Більш того, нехай ми припустимо, що принаймні одна з чисел непарна. Якщо це не справа, то нумер і деномінатор дроби завжди можна зменшити на 2 (потрібна кількість разів).
Далі ми отримуємо:
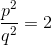
звідси:
Так це навіть число. А потім це навіть.
За умови непарності принаймні одного з чисел ми отримуємо це - непарно.
За рахунок парності можна писати
й
де є ціле.
А потім:
Головна
Але це означає, що він навіть, і тому навіть. Контрадикція.
Номер не може бути представлений як співвідношення двох цілих чисел.
Залишилося додавати, що це не дивно. Це може бути показано, що є більш раціональні числа, ніж раціональні. До речі, більш-менше співвідношення в світі нескінченних наборів є дуже протитуційним. Але це ще одна історія.
ПС. Я приймаю цю можливість привітати Хабровітів на наступ. Успіхів у новому році!
Джерело: habrahabr.ru/post/246963/
Термобар’єри, надгробки та інші шармії друкованих плат
Коли потрібні технології: як розвивати ІТ у 1985 році