804
对角线的平方
复数的引入不在人性号的认识的第一次革命。对于在此之前强大的冲击2000年体验希腊数学的世界。
麻烦开始了毕达哥拉斯学派并没有立即。毕达哥拉斯创立了科学的学校,最终严重结束,但今天的故事是不是快乐的大屠杀致力于在毕达哥拉斯学派感谢人民的教育,这和更大程度的精神波折。
有关毕达哥拉斯成立一个组织所谓“科学派”,就是一款这样的委婉说法。明智地通过看它的结构和应用技术,毕达哥拉斯安全地归因于极权主义邪教,这是相当在的时代精神(但是,它始终走在时代,永恒经典的精神)。出席并启动分离的程度,仪式与限制一个复杂的系统(例如,知名的,如“没有豆”或“不从整个面包咬掉”),和复杂的哲学学说。喜罗恩贺伯特的同伴。太阳底下没有新鲜事。
在一般情况下,毕达哥拉斯的生命在他的“学校”是坚实的,现在,除了有一个显著不断增长的政治影响力。
在一般情况下,毕达哥拉斯的理念,对西方文化的影响显著(和我们一样)。许多想法已经开发古希腊哲学和已经知道的一切勾股定理。表达“和谐球体”,顺便也可以追溯到毕达哥拉斯学派。
一个他们的哲学的基本要素是,任何数量的可被表示为两个整数的比率,这是一个简单的分数的想法。在这一点,他们,包括完美锯性质。此外,这似乎是相当明显的。在现代数学这样的数字称为理性的,他们集用符号 。让现在停顿了几秒钟,想想,所有应该的,这是不是真的?你可以给一个说法,这将是足够说服力的古希腊人?或者,至少,足够的说服力自己,亲自?
一般来说,数字的世界是简单的,优雅的,每个人都感到高兴。麻烦之源出人意料地出现,已经成为上述定理,它承担着毕达哥拉斯,最重要的现存之一,他的成就的名字。不幸的是,勾股定理的证明,我们不知道。现存最古老的 - 给出了欧几里德的“元素”并注明日期3。 BC让我提醒你,毕达哥拉斯自己生活在公元6世纪。 BC
梵蒂冈手稿号码190片段,10日。 BC (完全<一href="http://www.ibiblio.org/expo/vatican.exhibit/exhibit/d-mathematics/Greek_math.html">здесь):
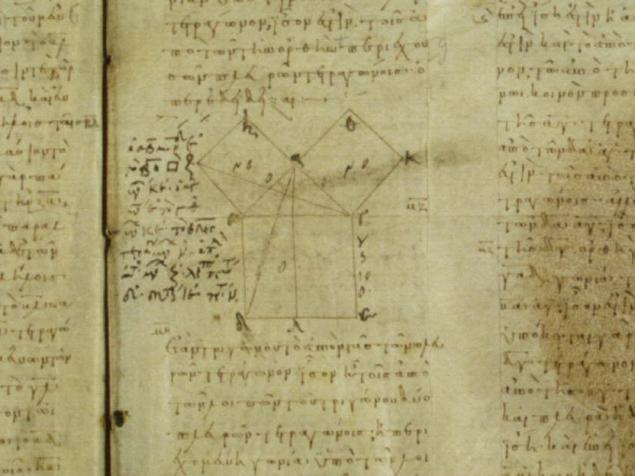
欧几里得的证明并不是一件容易的事。我们有理由相信,他知道的方式,更容易,但由于方法学方面的考虑导致了此选项,显示,除了勾股定理,和其他一些有趣的想法。
然而,回到毕达哥拉斯学派。
试想一下,一个简单的事情:与长的正方形。如果我们表示的对角线的长度,勾股定理我们得到:
并据此:
不言而喻的东西本身是没有问题的。但从毕达哥拉斯学派的角度来看,我们将只需要找到整数,这样
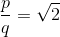
在这里,对这种“简单”的点,一切都停下来。紧。这一直持续到止动,直到一个聪明的人(据说希帕索斯也勾股定理),没有证明,突然间,这些数字是不存在的。所有的邪恶来自宏大的很多聪明的,你也知道。据传说,这个科学成就如此震惊的同事说,以纪念表彰科学价值的,无延迟希帕索斯扔到海里,当时他是在他的数学见解航行。但是,没有什么破坏尊敬的人,破坏如此钟爱培育的基础和理念高利润的系统。
现在,数并不表示为两个整数的比率,称为非理性。
一段时间甚至毕达哥拉斯学派保密的事实不合理。然而,纸包不住火了,真理是蛮快的(按历史标准衡量)已经找到了出路。
证明非理性并不困难。
假设存在使得
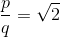
此外,我们假设中的至少一个的数字 - 奇。如果不是这种情况下,该分子和分母总是可以通过2(时间适量)减少。
然后,我们得到:
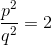
位置:
因此, - 一个偶数。但是 - 即使
。
通过假设,数字中的至少一个的奇怪,我们发现, - 奇
通过校验可以写
,
在那里 - 一个整体
。 但是:
因此
但是,这意味着, - 甚至,即使如此。矛盾。
数的不可能 i>的表示为两个整数的比值。
它仍然补充说 - 这是不是有些奇怪的怪胎。它可以使更多的无理数比合理,更从根本上进行显示。顺便说一下,该比率大于,小于在无限集合世界本身是非常kontrituitivnym。但是,这是另一个故事。
PS。我借此机会祝贺habrovchan就快到了。好运气在新的一年!
来源: habrahabr.ru/post/246963/
麻烦开始了毕达哥拉斯学派并没有立即。毕达哥拉斯创立了科学的学校,最终严重结束,但今天的故事是不是快乐的大屠杀致力于在毕达哥拉斯学派感谢人民的教育,这和更大程度的精神波折。
有关毕达哥拉斯成立一个组织所谓“科学派”,就是一款这样的委婉说法。明智地通过看它的结构和应用技术,毕达哥拉斯安全地归因于极权主义邪教,这是相当在的时代精神(但是,它始终走在时代,永恒经典的精神)。出席并启动分离的程度,仪式与限制一个复杂的系统(例如,知名的,如“没有豆”或“不从整个面包咬掉”),和复杂的哲学学说。喜罗恩贺伯特的同伴。太阳底下没有新鲜事。
在一般情况下,毕达哥拉斯的生命在他的“学校”是坚实的,现在,除了有一个显著不断增长的政治影响力。
在一般情况下,毕达哥拉斯的理念,对西方文化的影响显著(和我们一样)。许多想法已经开发古希腊哲学和已经知道的一切勾股定理。表达“和谐球体”,顺便也可以追溯到毕达哥拉斯学派。
一个他们的哲学的基本要素是,任何数量的可被表示为两个整数的比率,这是一个简单的分数的想法。在这一点,他们,包括完美锯性质。此外,这似乎是相当明显的。在现代数学这样的数字称为理性的,他们集用符号 。让现在停顿了几秒钟,想想,所有应该的,这是不是真的?你可以给一个说法,这将是足够说服力的古希腊人?或者,至少,足够的说服力自己,亲自?
一般来说,数字的世界是简单的,优雅的,每个人都感到高兴。麻烦之源出人意料地出现,已经成为上述定理,它承担着毕达哥拉斯,最重要的现存之一,他的成就的名字。不幸的是,勾股定理的证明,我们不知道。现存最古老的 - 给出了欧几里德的“元素”并注明日期3。 BC让我提醒你,毕达哥拉斯自己生活在公元6世纪。 BC
梵蒂冈手稿号码190片段,10日。 BC (完全<一href="http://www.ibiblio.org/expo/vatican.exhibit/exhibit/d-mathematics/Greek_math.html">здесь):

欧几里得的证明并不是一件容易的事。我们有理由相信,他知道的方式,更容易,但由于方法学方面的考虑导致了此选项,显示,除了勾股定理,和其他一些有趣的想法。
然而,回到毕达哥拉斯学派。
试想一下,一个简单的事情:与长的正方形。如果我们表示的对角线的长度,勾股定理我们得到:
并据此:
不言而喻的东西本身是没有问题的。但从毕达哥拉斯学派的角度来看,我们将只需要找到整数,这样
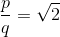
在这里,对这种“简单”的点,一切都停下来。紧。这一直持续到止动,直到一个聪明的人(据说希帕索斯也勾股定理),没有证明,突然间,这些数字是不存在的。所有的邪恶来自宏大的很多聪明的,你也知道。据传说,这个科学成就如此震惊的同事说,以纪念表彰科学价值的,无延迟希帕索斯扔到海里,当时他是在他的数学见解航行。但是,没有什么破坏尊敬的人,破坏如此钟爱培育的基础和理念高利润的系统。
现在,数并不表示为两个整数的比率,称为非理性。
一段时间甚至毕达哥拉斯学派保密的事实不合理。然而,纸包不住火了,真理是蛮快的(按历史标准衡量)已经找到了出路。
证明非理性并不困难。
假设存在使得
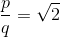
此外,我们假设中的至少一个的数字 - 奇。如果不是这种情况下,该分子和分母总是可以通过2(时间适量)减少。
然后,我们得到:
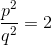
位置:
因此, - 一个偶数。但是 - 即使
。
通过假设,数字中的至少一个的奇怪,我们发现, - 奇
通过校验可以写
,
在那里 - 一个整体
。 但是:
因此
但是,这意味着, - 甚至,即使如此。矛盾。
数的不可能 i>的表示为两个整数的比值。
它仍然补充说 - 这是不是有些奇怪的怪胎。它可以使更多的无理数比合理,更从根本上进行显示。顺便说一下,该比率大于,小于在无限集合世界本身是非常kontrituitivnym。但是,这是另一个故事。
PS。我借此机会祝贺habrovchan就快到了。好运气在新的一年!
来源: habrahabr.ru/post/246963/