1634
不安的素数:编织的秘密社团的秘密
不安的素数

笔者提供了一个窥探到的是一组素数,如果你看看他们的几何形状。这不是一个专业的工作,但一些有趣的图案简单,业余学习。因此,本文将不复杂的数学,我们不会爬深入到她的丛林。在一般情况下,如果你不十分熟悉的素数,其结构和百年历史的研究数论,这篇文章 - 你。

我要强调特别是对于熟练的数学家和谁自己适用于他们的读者:文章是不是一个专业的工作。这是一些特性,合数的模式的图示,仅用于识别和强调对结构模式的说明的目的,然后可以解析地表示 i>的
大概的读者熟悉许多与素数有关的问题。其在该组自然数的位置不明显。大素数是很难找到,你需要很多的努力来检查了大量的它的简单。这一困难是基于,密码学的许多现代方法。我们可以很容易繁殖是多值的素数,但我们知道,结果发现,原来因素 - 一个非常艰巨的任务。
有许多方式来优化简单排序快得多,但即使在最优化的搜索将加速到10倍,足以小数位的数目增加为2(即,100)以减慢搜索中的100倍。
这意味着,该算法的复杂度指数,所以不管有多快,或者在一台超级计算机,我们可以选择更多的这些超级计算机的长度了十亿。诚然,有必要再次澄清:找到素数相乘就变成只是越来越难做
。
顺便说一下,数学家没有发现任何证据,也没有否认,这是不可能找到一个分解算法的复杂性,其中不会指数依赖于数的长度。和证明或反驳它,由于一些相信数学,可以同时获得,以解决被称为黎曼假设一个数学问题。其证明克雷数学研究所答应一百万美元。虽然它很可能是该因子分解问题将多项式,但黎曼假设是既不证实,也不反驳。
如果阴影多少?
丢弃 因为我们不知道法律通过它方便地找到素数,也许细看数字组成的模式?从数学上来说,我们认为该组自然数,即附加到组简单。
这个想法是很简单的合数。花几分钟的自然数和繁殖他们。因此,我们得到一个合数。
我们很容易找到无穷大合数,只需通过2
乘以ñ

由3.
同样适用于乘法

其次是4,但在这里,我们没有发现新的数字,它们都具有平等的2n个。其次5N,然后6N,这是我们发现的两倍,2N和3N时间。它并不增加合数的数量,但会导致我们相信,合数的图案中包含的产品简单。
但是,如果我们走远一点,我们发现一个有趣的模式:6号是2和3的产品这就意味着我们将有许多便利就在合数表:
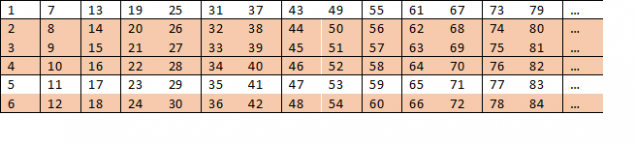
看着桌子上,我们了解到,在线路2,3,4和6可能永远是素数。这意味着,找到一个素数的概率不超过2/6。我们认识到数字,这个概率更小,但多少?
试图继续寻找合数的合适的结构,为此,想想这意味着什么2×3 = 6?如果我们采取2h3h5产品的基础?我们得到如下有趣的表(所以它不会占用太多的空间,减少字体):
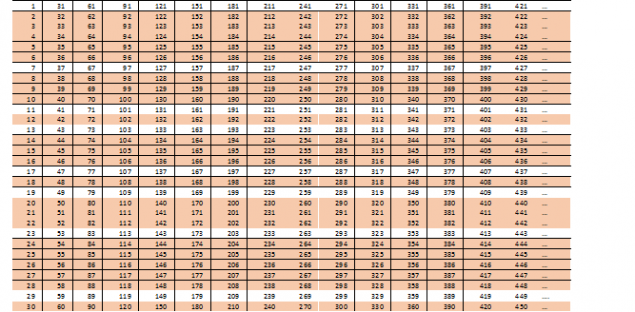
我们可以看到:
- 15线的形式为2n,
- 5号线的形式3N的(6N + 5种已经包含在2N)
- 与2号线的形式5N(三个品种10N已经删除的号码2N和一个线路之间的15N 3N)
不能包含素数(我们预计,对吧?)
只有8行的形式30N +我,其中i = 1,7,11,13,17,19,23,29,如果你看看在他们的对称性就可以看出。 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17。
因此,可以写成紧凑30N + - 我,其中i = 1,7,11,13,17
我们明白,找到一个任意素数不超过8/30的概率。在2/30少...
下一步是什么?逻辑上,下表中应该2h3h5h7 = 210行。进一步210h11 = 2310,然后2310h13,所以我们将始终如一地乘素数,越来越大基地“横”,将保留其绑扎。
它看起来好象素投下“阴影”为无穷大他们多个号码是当它们存在,放置在一排分别是基部,我们表示为P(i)中,等于i个连续的素数的乘积。
由此可以看出,该带状线位于第一和下一个,它可以包含一个简单的数字之间正在以一种非常简单的法则:如果线6,即2×3,素数可,是在第5行,如果2h3h5,然后从第7行开始,这是合乎逻辑的。因此,在与第一行之后的行30 030(2h3h5h7h11h13)的数目的矩阵是宽频带的组合数字,到下一个17行数如果我们把矩阵9699690行(2h3h5h7h11h13h17h19),条带,其中质数无拉伸到线21作为典型的对称,因为,基体的底部也将20行只用合数。
多维矩阵和超写实分形?
但什么是这些作品? 2×3 - 用6 2h3h5一个区域的矩形 - 平行六面体体积30.然后呢? 2h3h5h7 - giperparallelepiped 4尺寸,超体积210?进而? 5测量,6,......无限?
只是觉得有什么可以想像的多维世界中,素数投下自己的影子在所有方面......
我们可以想象四个或更多维度,投射到一个平面上或在三维空间中,例如,扩大的矩阵,如在边缘轧制的多维超立方体与面,并考虑在纸张上产生的印刷(以及得到的部分的打印)。
这里是最初方面:

但它的扫描两面:

很清楚,在所有正确的超平面,我们只合数。它甚至不能行驶。你可以看看其他的扫描,查看“从上面”,但我们去进一步进入一个更有趣的方向发展。
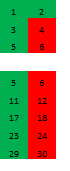
现在让我们尝试将映像部署到第四维,我们感兴趣的是,在那里你可以找到素数的方向:

这里褐色颜色表示的形式的Mn,其中编号的作品,从11至19(最近的整数小于十一分之二百十)的数量。这些数字的特点是,他们是不是素数不是“投射阴影”深入到下一个层面。
我们可以看到,中间层扫再次变得微不足道 - 以下素数不是。但外边缘giperpallelepipeda可以进一步考虑。该矩阵的每一列被分解在7H11,得到5这些矩阵的每一个3x5的矩阵的三个层(此处显示扫描一列,所述矩阵的第二列的片段):
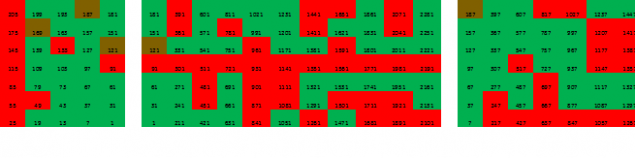
然后进入测量扫描的例子中,我们不会,根据第二十将是不明智的。在文章的最后,你可以看看一些插图。我们希望,这项研究稍微醒你的想象力和之旅的艰难的世界,素数你喜欢,似乎有帮助的。
结论
此外,笔者要指出,这种方法的持续研究。例如,问题出现在更大的矩阵工作,在深和体积的预测以蒙上了一层阴影下一次测量增加新的质数号码的第三,第四和进一步的权力,而仍然是一个“点”的夹杂物。
但也许是最有趣的是进一步核实,并进一步寻找素数的概率估计的可能性。如果我们考虑到基质中,我们看到跌倒的可能性,从4/6,然后到7/24(或平均11/30),然后一百八分之三十六(或二百一分之四十七)等
此外,作者具有分解算法,所述优化是一个多维矩阵可以显著加快它(但这不不再有字符降解的数量的难度指数度)。
算法本身是基于一个很简单的。
取两个连续奇数,p和q,使得PQ靠近X(舍入用于的奇数的较大和较小的根的X,其条件是X不是正方形)。先前,我们消除了奇偶X(除以2,只要结果是偶数),得到因子2 ^ K。另外,在循环检查X和PQ之间的差异。如果它是零 - 结果获得的。如果它是大于零,我们减少Q上2.如果小于零,我们增加P由2Q。环路仅此外,这样的算法是相当快的(只依赖于实现与BigInteger的函数)。
然而,作者推测的转化步骤可显著而不损失精度,如果我们使用基重数增加。 X是两个连续的P(i)和P(i + 1的),其中n(I)之间的任何数字 - 第一个素数i的乘积,所以可以判断,其中肋的X数字并且其由对更近范围和自由中的q每个突起),因此,形成的p和q中的一个平面部的矩形的giperparallelepipeda扩大。
附:什么是织工的秘密社团,读者会问,谁提请原题?读者可能还记得电影“通缉令”,今年有望更......在这部影片中,使织机的预测,把线程和节...看看它是如何使类似的素弦...
矩阵30h7:

和一块矩阵210h11的:
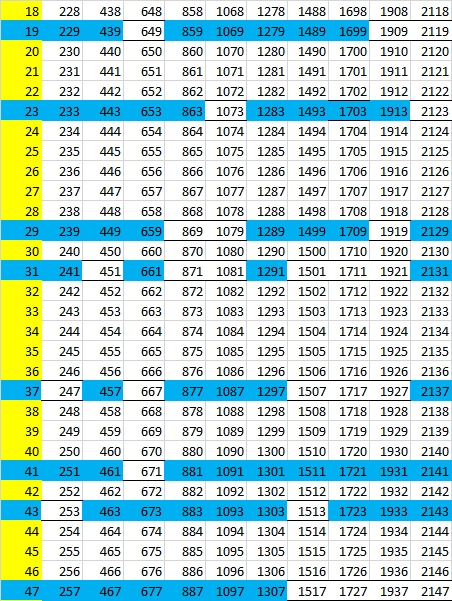
而这款机器的控制结节这里有矩阵打孔卡。扫描的2x3矩阵:

而更多的,引脚6x5矩阵:

来源: habrahabr.ru/post/255527/

笔者提供了一个窥探到的是一组素数,如果你看看他们的几何形状。这不是一个专业的工作,但一些有趣的图案简单,业余学习。因此,本文将不复杂的数学,我们不会爬深入到她的丛林。在一般情况下,如果你不十分熟悉的素数,其结构和百年历史的研究数论,这篇文章 - 你。

我要强调特别是对于熟练的数学家和谁自己适用于他们的读者:文章是不是一个专业的工作。这是一些特性,合数的模式的图示,仅用于识别和强调对结构模式的说明的目的,然后可以解析地表示 i>的
大概的读者熟悉许多与素数有关的问题。其在该组自然数的位置不明显。大素数是很难找到,你需要很多的努力来检查了大量的它的简单。这一困难是基于,密码学的许多现代方法。我们可以很容易繁殖是多值的素数,但我们知道,结果发现,原来因素 - 一个非常艰巨的任务。
有许多方式来优化简单排序快得多,但即使在最优化的搜索将加速到10倍,足以小数位的数目增加为2(即,100)以减慢搜索中的100倍。
这意味着,该算法的复杂度指数,所以不管有多快,或者在一台超级计算机,我们可以选择更多的这些超级计算机的长度了十亿。诚然,有必要再次澄清:找到素数相乘就变成只是越来越难做
。
顺便说一下,数学家没有发现任何证据,也没有否认,这是不可能找到一个分解算法的复杂性,其中不会指数依赖于数的长度。和证明或反驳它,由于一些相信数学,可以同时获得,以解决被称为黎曼假设一个数学问题。其证明克雷数学研究所答应一百万美元。虽然它很可能是该因子分解问题将多项式,但黎曼假设是既不证实,也不反驳。
如果阴影多少?
丢弃 因为我们不知道法律通过它方便地找到素数,也许细看数字组成的模式?从数学上来说,我们认为该组自然数,即附加到组简单。
这个想法是很简单的合数。花几分钟的自然数和繁殖他们。因此,我们得到一个合数。
我们很容易找到无穷大合数,只需通过2
乘以ñ

由3.
同样适用于乘法

其次是4,但在这里,我们没有发现新的数字,它们都具有平等的2n个。其次5N,然后6N,这是我们发现的两倍,2N和3N时间。它并不增加合数的数量,但会导致我们相信,合数的图案中包含的产品简单。
但是,如果我们走远一点,我们发现一个有趣的模式:6号是2和3的产品这就意味着我们将有许多便利就在合数表:

看着桌子上,我们了解到,在线路2,3,4和6可能永远是素数。这意味着,找到一个素数的概率不超过2/6。我们认识到数字,这个概率更小,但多少?
试图继续寻找合数的合适的结构,为此,想想这意味着什么2×3 = 6?如果我们采取2h3h5产品的基础?我们得到如下有趣的表(所以它不会占用太多的空间,减少字体):

我们可以看到:
- 15线的形式为2n,
- 5号线的形式3N的(6N + 5种已经包含在2N)
- 与2号线的形式5N(三个品种10N已经删除的号码2N和一个线路之间的15N 3N)
不能包含素数(我们预计,对吧?)
只有8行的形式30N +我,其中i = 1,7,11,13,17,19,23,29,如果你看看在他们的对称性就可以看出。 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17。
因此,可以写成紧凑30N + - 我,其中i = 1,7,11,13,17
我们明白,找到一个任意素数不超过8/30的概率。在2/30少...
下一步是什么?逻辑上,下表中应该2h3h5h7 = 210行。进一步210h11 = 2310,然后2310h13,所以我们将始终如一地乘素数,越来越大基地“横”,将保留其绑扎。
它看起来好象素投下“阴影”为无穷大他们多个号码是当它们存在,放置在一排分别是基部,我们表示为P(i)中,等于i个连续的素数的乘积。
由此可以看出,该带状线位于第一和下一个,它可以包含一个简单的数字之间正在以一种非常简单的法则:如果线6,即2×3,素数可,是在第5行,如果2h3h5,然后从第7行开始,这是合乎逻辑的。因此,在与第一行之后的行30 030(2h3h5h7h11h13)的数目的矩阵是宽频带的组合数字,到下一个17行数如果我们把矩阵9699690行(2h3h5h7h11h13h17h19),条带,其中质数无拉伸到线21作为典型的对称,因为,基体的底部也将20行只用合数。
多维矩阵和超写实分形?
但什么是这些作品? 2×3 - 用6 2h3h5一个区域的矩形 - 平行六面体体积30.然后呢? 2h3h5h7 - giperparallelepiped 4尺寸,超体积210?进而? 5测量,6,......无限?
只是觉得有什么可以想像的多维世界中,素数投下自己的影子在所有方面......
我们可以想象四个或更多维度,投射到一个平面上或在三维空间中,例如,扩大的矩阵,如在边缘轧制的多维超立方体与面,并考虑在纸张上产生的印刷(以及得到的部分的打印)。
这里是最初方面:

但它的扫描两面:

很清楚,在所有正确的超平面,我们只合数。它甚至不能行驶。你可以看看其他的扫描,查看“从上面”,但我们去进一步进入一个更有趣的方向发展。

现在让我们尝试将映像部署到第四维,我们感兴趣的是,在那里你可以找到素数的方向:

这里褐色颜色表示的形式的Mn,其中编号的作品,从11至19(最近的整数小于十一分之二百十)的数量。这些数字的特点是,他们是不是素数不是“投射阴影”深入到下一个层面。
我们可以看到,中间层扫再次变得微不足道 - 以下素数不是。但外边缘giperpallelepipeda可以进一步考虑。该矩阵的每一列被分解在7H11,得到5这些矩阵的每一个3x5的矩阵的三个层(此处显示扫描一列,所述矩阵的第二列的片段):

然后进入测量扫描的例子中,我们不会,根据第二十将是不明智的。在文章的最后,你可以看看一些插图。我们希望,这项研究稍微醒你的想象力和之旅的艰难的世界,素数你喜欢,似乎有帮助的。
结论
此外,笔者要指出,这种方法的持续研究。例如,问题出现在更大的矩阵工作,在深和体积的预测以蒙上了一层阴影下一次测量增加新的质数号码的第三,第四和进一步的权力,而仍然是一个“点”的夹杂物。
但也许是最有趣的是进一步核实,并进一步寻找素数的概率估计的可能性。如果我们考虑到基质中,我们看到跌倒的可能性,从4/6,然后到7/24(或平均11/30),然后一百八分之三十六(或二百一分之四十七)等
此外,作者具有分解算法,所述优化是一个多维矩阵可以显著加快它(但这不不再有字符降解的数量的难度指数度)。
算法本身是基于一个很简单的。
取两个连续奇数,p和q,使得PQ靠近X(舍入用于的奇数的较大和较小的根的X,其条件是X不是正方形)。先前,我们消除了奇偶X(除以2,只要结果是偶数),得到因子2 ^ K。另外,在循环检查X和PQ之间的差异。如果它是零 - 结果获得的。如果它是大于零,我们减少Q上2.如果小于零,我们增加P由2Q。环路仅此外,这样的算法是相当快的(只依赖于实现与BigInteger的函数)。
然而,作者推测的转化步骤可显著而不损失精度,如果我们使用基重数增加。 X是两个连续的P(i)和P(i + 1的),其中n(I)之间的任何数字 - 第一个素数i的乘积,所以可以判断,其中肋的X数字并且其由对更近范围和自由中的q每个突起),因此,形成的p和q中的一个平面部的矩形的giperparallelepipeda扩大。
附:什么是织工的秘密社团,读者会问,谁提请原题?读者可能还记得电影“通缉令”,今年有望更......在这部影片中,使织机的预测,把线程和节...看看它是如何使类似的素弦...
矩阵30h7:

和一块矩阵210h11的:

而这款机器的控制结节这里有矩阵打孔卡。扫描的2x3矩阵:

而更多的,引脚6x5矩阵:

来源: habrahabr.ru/post/255527/