1695
Uneasy primes: Secrets of the secret society of weavers
Uneasy primes

The author offers a glimpse into what is a set of primes, if you look at their geometric form. This is not a professional job, but a simple, amateur study of some interesting patterns. Therefore, the article will not be complicated mathematics, and we will not climb deep into her jungle. In general, if you are not intimately familiar with prime numbers, their structure and the centuries-old research in number theory, this article - for you.

I stress especially for skilled mathematicians and those readers who themselves applies to them: article is not a professional job. This is an illustration of some properties and patterns of composite numbers, for illustrative purposes only and identifying patterns of emphasis on structure, which can then be expressed analytically i>
Probably the reader is familiar with many of the problems associated with primes. Their location in the set of natural numbers is not obvious. Large prime numbers is difficult to find, you need a lot of effort to check a large number of its simplicity. This difficulty is based, many modern methods of cryptography. We can easily multiply yes multivalued primes, but knowing the result to find the original factors - a very difficult task.
There are many ways to optimize that simple sorting is much faster, but even if the optimization search will accelerate to 10 times, is sufficient to increase the number of decimal places to 2 (i.e., 100) to slow down the search in 100 times.
This means that the complexity of the algorithm is exponential, so no matter how fast or was a supercomputer, we can choose the length of more to these supercomputers took billion. True, it is necessary to clarify once again: find prime numbers to multiply then becomes just getting harder and harder.
By the way, mathematicians did not find any evidence nor denied that it is impossible to find a factorization algorithm, the complexity of which would not be exponentially dependent on the length of the number. And proving or disproving it, as some believe mathematics, can be obtained at the same time, to solve a mathematical problem known as the Riemann hypothesis. For its proof Clay Mathematics Institute promised a million dollars. While it may well be that the factorization problem will polynomial, but the Riemann hypothesis is neither prove nor disprove.
Discarded if the number of shadows?
Since we do not know the laws by which to easily find prime numbers, maybe look closely at the patterns of numbers constituents? Mathematically speaking, we consider the set of natural numbers, that is additional to the set of simple.
The idea is very simple composite numbers. Take a few natural numbers and multiply them. Thus, we get a composite number.
We are easy to find infinity composite numbers, simply by multiplying n by 2.

The same applies to multiplication by 3.

Followed by 4, but here we do not find new numbers, they all have equal 2n. Followed 5n, then 6n, which we found twice as 2n and 3n time. It does not increase the number of composite numbers, but leads us to believe that the pattern of composite numbers is contained in the product simple.
But if we go a little further, we find an interesting pattern: the number 6 is the product of 2 and 3. This means that we will have many conveniently located right in the table of composite numbers:
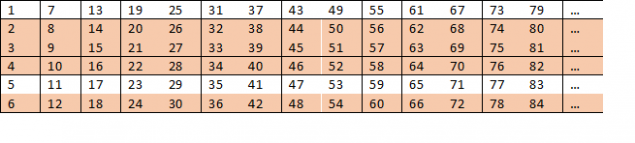
Looking at the table, we understand that in lines 2, 3, 4 and 6 may never be prime numbers. This means that the probability of finding a prime number can not exceed 2/6. We realize that the numbers, this probability is even smaller, but how much?
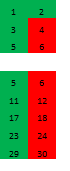
Try to continue to look for a suitable structure of composite numbers, and for this, think about what it means to 2x3 = 6? What if we take the product of 2h3h5 a basis? We obtain the following interesting table (so it does not take up much space, decrease font):

We can see that:
- 15 lines of the form 2n,
- 5 lines of the form 3n (6n + 5 species already included in 2n)
- And 2 lines of the form 5n (three species 10n already deleted in numbers 2n and one among the lines 15n 3n)
can not contain primes (we expected this, right?)
There are only eight rows form 30n + i, where i = 1, 7, 11, 13, 17, 19, 23, 29. If you look in the symmetry of them can be seen. 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17.
Therefore, as can be written compactly 30n + - i, where i = 1, 7, 11, 13, 17
And we understand that the probability of finding an arbitrary prime number not more than 8/30. On 2/30 fewer ...
What next? Logically, in the following table should be 2h3h5h7 = 210 lines. Even further 210h11 = 2310 then 2310h13, and so we will consistently multiply primes, getting larger and larger base "horizontal", which will retain its banding.
It looks as if the primes cast "shadows" to infinity them multiple numbers if they are placed in a row, respectively, of the base, which we denote by P (i), equal to the product of i consecutive primes.
It can be seen that the strip lines lying between the first and the next, which can contain a simple number is growing at a very simple law: if the lines 6, that is 2x3, the primes can be in line 5, if 2h3h5, then starting from row 7 , which is logical. Thus, in a matrix with the number of rows 30 030 (2h3h5h7h11h13) after the first line is the broad band composite numbers, to the line number of the next 17. If we take the matrix to 9,699,690 rows (2h3h5h7h11h13h17h19), the strip where primes no stretch to line 21. As is typical, because of the symmetry, the bottom of the matrix will also be 20 lines with only composite numbers.
Multi-dimensional matrix and hyperrealism fractals?
But what are these works? 2x3 - a rectangle with an area of 6 2h3h5 - parallelepiped volume 30. And then? 2h3h5h7 - giperparallelepiped in 4 dimensions, with hypervolume 210? And then? 5 measurements, 6, ... Infinity?
Just think what could have imagined multidimensional world in which primes cast their shadows in all dimensions ...
We can imagine four or more dimensions, projected onto a plane or in three-dimensional space, for example, expanding the matrix, like rolling a multi-dimensional hypercube with faces on the brink, and considering the resulting prints on paper (as well as getting prints of sections).
Here are the initial facet:

But its scan both sides:

Very well, that in all the right hyperplane we only composite numbers. It can not even travel. You can look at other scan, view "from above", but we go further into a more interesting direction.
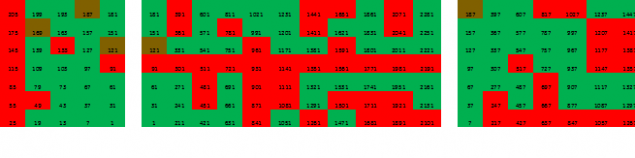
Let us now try to deploy the image to the fourth dimension, we are interested in the direction of where you can find prime numbers:

Here brown color indicates the number of the form mn, which compiled the works of numbers from 11 to 19 (the nearest integer less than 210/11). The peculiarity of these numbers is that they are not being primes not "cast shadows" deep into the next dimension.
As we can see, the middle layer sweep again becomes trivial - hereinafter primes not. But the outer edges giperpallelepipeda can be considered further. Each column of the matrix is decomposed in 7h11, get 5 of these matrices for each of the three layers of 3x5 matrix (shown here scan of one column and a fragment of the matrix for the second column):
Then go into measuring the example of scan we will not, under Article would be unwise. At the end of the article, you can look at a few illustrations. Hopefully, this study slightly woke your imagination and journey into the world of difficult and primes you liked and seemed helpful.
Conclusion
In addition, the author wishes to note that the continued study of this method. For example, the questions appear in the larger matrices works third, fourth and further powers of numbers that add new prime numbers in the deep and volume projections as to cast a shadow over the next measurement, and remains a "point" inclusions.
But perhaps the most interesting is the possibility of verifying estimates of the probability of finding prime numbers further and further. If we consider the matrix, we see the probability of falls, starting with 4/6, then to 7/24 (or averaged 11/30), then 36/180 (or 47/210), etc.
In addition, the author has a factorization algorithm, the optimization is a multi-dimensional matrix can significantly speed it up (but this does not cease to have an exponential degree of difficulty of the number of characters degradable).
The algorithm itself is based on a very simple.
Take two successive odd numbers, p and q, such that pq close to X (Rounding is used to root X of the larger and smaller of odd numbers, with the proviso that X is not a square). Previously, we eliminate the parity X (divide by 2 as long as the result is even) to give the factor 2 ^ K. Further, in the loop check the difference between X and pq. If it is zero - the result obtained. If it is greater than zero, we reduce q on 2. If less than zero, we increase p by 2q. The loop only addition, so the algorithm is quite fast (depends only on the realization of functions with BigInteger).
However, the author has hypothesized that the conversion step can be increased significantly without loss of accuracy if we use the base multiplicity. X is any number between two consecutive P (i) and P (i + 1), where n (i) - the product of the first prime number i, so it can be determined which of the X number of the ribs and which is closer range and freedom from p q in each projection) and thus formed p and q of a rectangle in one plane section giperparallelepipeda expand.
P.S. And what are the secret society of weavers, the reader will ask, who drew the original title? The reader may remember the movie "Wanted" this year promises even more ... In this film loom makes predictions, putting threads and knots ... Look how similar it makes strings of primes ...
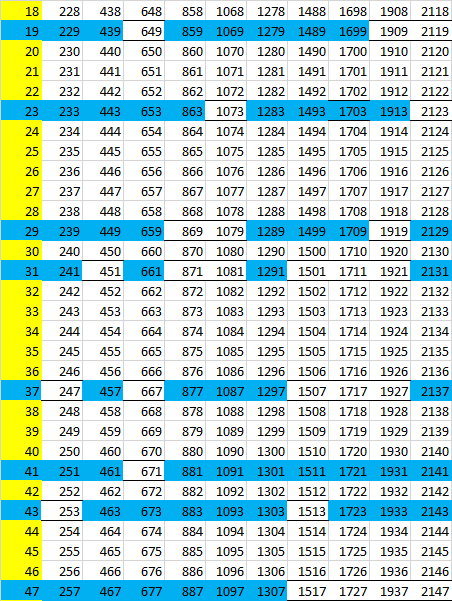
The matrix 30h7:

And a piece of matrix 210h11:
And this machine is controlled nodules here are matrix-punch cards. Scan 2x3 matrices:

And more, 6x5 matrices:

Source: habrahabr.ru/post/255527/

The author offers a glimpse into what is a set of primes, if you look at their geometric form. This is not a professional job, but a simple, amateur study of some interesting patterns. Therefore, the article will not be complicated mathematics, and we will not climb deep into her jungle. In general, if you are not intimately familiar with prime numbers, their structure and the centuries-old research in number theory, this article - for you.

I stress especially for skilled mathematicians and those readers who themselves applies to them: article is not a professional job. This is an illustration of some properties and patterns of composite numbers, for illustrative purposes only and identifying patterns of emphasis on structure, which can then be expressed analytically i>
Probably the reader is familiar with many of the problems associated with primes. Their location in the set of natural numbers is not obvious. Large prime numbers is difficult to find, you need a lot of effort to check a large number of its simplicity. This difficulty is based, many modern methods of cryptography. We can easily multiply yes multivalued primes, but knowing the result to find the original factors - a very difficult task.
There are many ways to optimize that simple sorting is much faster, but even if the optimization search will accelerate to 10 times, is sufficient to increase the number of decimal places to 2 (i.e., 100) to slow down the search in 100 times.
This means that the complexity of the algorithm is exponential, so no matter how fast or was a supercomputer, we can choose the length of more to these supercomputers took billion. True, it is necessary to clarify once again: find prime numbers to multiply then becomes just getting harder and harder.
By the way, mathematicians did not find any evidence nor denied that it is impossible to find a factorization algorithm, the complexity of which would not be exponentially dependent on the length of the number. And proving or disproving it, as some believe mathematics, can be obtained at the same time, to solve a mathematical problem known as the Riemann hypothesis. For its proof Clay Mathematics Institute promised a million dollars. While it may well be that the factorization problem will polynomial, but the Riemann hypothesis is neither prove nor disprove.
Discarded if the number of shadows?
Since we do not know the laws by which to easily find prime numbers, maybe look closely at the patterns of numbers constituents? Mathematically speaking, we consider the set of natural numbers, that is additional to the set of simple.
The idea is very simple composite numbers. Take a few natural numbers and multiply them. Thus, we get a composite number.
We are easy to find infinity composite numbers, simply by multiplying n by 2.

The same applies to multiplication by 3.

Followed by 4, but here we do not find new numbers, they all have equal 2n. Followed 5n, then 6n, which we found twice as 2n and 3n time. It does not increase the number of composite numbers, but leads us to believe that the pattern of composite numbers is contained in the product simple.
But if we go a little further, we find an interesting pattern: the number 6 is the product of 2 and 3. This means that we will have many conveniently located right in the table of composite numbers:

Looking at the table, we understand that in lines 2, 3, 4 and 6 may never be prime numbers. This means that the probability of finding a prime number can not exceed 2/6. We realize that the numbers, this probability is even smaller, but how much?
Try to continue to look for a suitable structure of composite numbers, and for this, think about what it means to 2x3 = 6? What if we take the product of 2h3h5 a basis? We obtain the following interesting table (so it does not take up much space, decrease font):

We can see that:
- 15 lines of the form 2n,
- 5 lines of the form 3n (6n + 5 species already included in 2n)
- And 2 lines of the form 5n (three species 10n already deleted in numbers 2n and one among the lines 15n 3n)
can not contain primes (we expected this, right?)
There are only eight rows form 30n + i, where i = 1, 7, 11, 13, 17, 19, 23, 29. If you look in the symmetry of them can be seen. 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17.
Therefore, as can be written compactly 30n + - i, where i = 1, 7, 11, 13, 17
And we understand that the probability of finding an arbitrary prime number not more than 8/30. On 2/30 fewer ...
What next? Logically, in the following table should be 2h3h5h7 = 210 lines. Even further 210h11 = 2310 then 2310h13, and so we will consistently multiply primes, getting larger and larger base "horizontal", which will retain its banding.
It looks as if the primes cast "shadows" to infinity them multiple numbers if they are placed in a row, respectively, of the base, which we denote by P (i), equal to the product of i consecutive primes.
It can be seen that the strip lines lying between the first and the next, which can contain a simple number is growing at a very simple law: if the lines 6, that is 2x3, the primes can be in line 5, if 2h3h5, then starting from row 7 , which is logical. Thus, in a matrix with the number of rows 30 030 (2h3h5h7h11h13) after the first line is the broad band composite numbers, to the line number of the next 17. If we take the matrix to 9,699,690 rows (2h3h5h7h11h13h17h19), the strip where primes no stretch to line 21. As is typical, because of the symmetry, the bottom of the matrix will also be 20 lines with only composite numbers.
Multi-dimensional matrix and hyperrealism fractals?
But what are these works? 2x3 - a rectangle with an area of 6 2h3h5 - parallelepiped volume 30. And then? 2h3h5h7 - giperparallelepiped in 4 dimensions, with hypervolume 210? And then? 5 measurements, 6, ... Infinity?
Just think what could have imagined multidimensional world in which primes cast their shadows in all dimensions ...
We can imagine four or more dimensions, projected onto a plane or in three-dimensional space, for example, expanding the matrix, like rolling a multi-dimensional hypercube with faces on the brink, and considering the resulting prints on paper (as well as getting prints of sections).
Here are the initial facet:

But its scan both sides:

Very well, that in all the right hyperplane we only composite numbers. It can not even travel. You can look at other scan, view "from above", but we go further into a more interesting direction.

Let us now try to deploy the image to the fourth dimension, we are interested in the direction of where you can find prime numbers:

Here brown color indicates the number of the form mn, which compiled the works of numbers from 11 to 19 (the nearest integer less than 210/11). The peculiarity of these numbers is that they are not being primes not "cast shadows" deep into the next dimension.
As we can see, the middle layer sweep again becomes trivial - hereinafter primes not. But the outer edges giperpallelepipeda can be considered further. Each column of the matrix is decomposed in 7h11, get 5 of these matrices for each of the three layers of 3x5 matrix (shown here scan of one column and a fragment of the matrix for the second column):

Then go into measuring the example of scan we will not, under Article would be unwise. At the end of the article, you can look at a few illustrations. Hopefully, this study slightly woke your imagination and journey into the world of difficult and primes you liked and seemed helpful.
Conclusion
In addition, the author wishes to note that the continued study of this method. For example, the questions appear in the larger matrices works third, fourth and further powers of numbers that add new prime numbers in the deep and volume projections as to cast a shadow over the next measurement, and remains a "point" inclusions.
But perhaps the most interesting is the possibility of verifying estimates of the probability of finding prime numbers further and further. If we consider the matrix, we see the probability of falls, starting with 4/6, then to 7/24 (or averaged 11/30), then 36/180 (or 47/210), etc.
In addition, the author has a factorization algorithm, the optimization is a multi-dimensional matrix can significantly speed it up (but this does not cease to have an exponential degree of difficulty of the number of characters degradable).
The algorithm itself is based on a very simple.
Take two successive odd numbers, p and q, such that pq close to X (Rounding is used to root X of the larger and smaller of odd numbers, with the proviso that X is not a square). Previously, we eliminate the parity X (divide by 2 as long as the result is even) to give the factor 2 ^ K. Further, in the loop check the difference between X and pq. If it is zero - the result obtained. If it is greater than zero, we reduce q on 2. If less than zero, we increase p by 2q. The loop only addition, so the algorithm is quite fast (depends only on the realization of functions with BigInteger).
However, the author has hypothesized that the conversion step can be increased significantly without loss of accuracy if we use the base multiplicity. X is any number between two consecutive P (i) and P (i + 1), where n (i) - the product of the first prime number i, so it can be determined which of the X number of the ribs and which is closer range and freedom from p q in each projection) and thus formed p and q of a rectangle in one plane section giperparallelepipeda expand.
P.S. And what are the secret society of weavers, the reader will ask, who drew the original title? The reader may remember the movie "Wanted" this year promises even more ... In this film loom makes predictions, putting threads and knots ... Look how similar it makes strings of primes ...
The matrix 30h7:

And a piece of matrix 210h11:

And this machine is controlled nodules here are matrix-punch cards. Scan 2x3 matrices:

And more, 6x5 matrices:

Source: habrahabr.ru/post/255527/
Overweight saves from acquired dementia
French television channel was hacked after the interview personnel background stickers with passwords