1645
Primos Uneasy: Secretos de la sociedad secreta de los tejedores
Primos Uneasy

El autor ofrece una visión de lo que es un conjunto de números primos, si nos fijamos en su forma geométrica. Esto no es un trabajo profesional, pero un estudio simple, aficionado de algunos patrones interesantes. Por lo tanto, el artículo no será complicada de las matemáticas, y no vamos a subir el fondo de su selva. En general, si usted no está muy familiarizado con los números primos, su estructura y la centenaria investigación en la teoría de números, en este artículo - para usted.

subrayo especialmente para los matemáticos especializados y aquellos lectores que sí se aplica a ellos: el artículo no es un trabajo profesional. Esta es una ilustración de algunas propiedades y patrones de números compuestos, únicamente para la identificación de patrones de énfasis en la estructura a efectos ilustrativos, que luego se pueden expresar analíticamente i>
Probablemente el lector está familiarizado con muchos de los problemas asociados con números primos. Su ubicación en el conjunto de números naturales no es obvia. Números primos grandes es difícil de encontrar, es necesario un gran esfuerzo para revisar una gran cantidad de su simplicidad. Esta dificultad se basa, muchos métodos modernos de la criptografía. Podemos multiplicar fácilmente primos sí de varios valores, pero sabiendo el resultado de encontrar los factores originales - una tarea muy difícil.
Hay muchas maneras de optimizar así de simple clasificación es mucho más rápido, pero incluso si la búsqueda de optimización se acelerará a 10 veces, es suficiente para aumentar el número de decimales a 2 (es decir, 100) para ralentizar la búsqueda en 100 veces.
Esto significa que la complejidad del algoritmo es exponencial, por lo que no importa qué tan rápido o era un superordenador, podemos elegir la longitud de más de estos superordenadores tomó millones de dólares. Es cierto que es necesario aclarar una vez más: encontrar números primos para multiplicar luego se convierte en sólo cada vez más difícil
.
Por cierto, los matemáticos no se encontró ninguna evidencia ni negar que es imposible encontrar un algoritmo de factorización, la complejidad de los cuales no sería dependiente de forma exponencial en la longitud del número. Y probar o refutar que, como algunos creen las matemáticas, se puede obtener, al mismo tiempo, para resolver un problema matemático conocido como la hipótesis de Riemann. Por su prueba Clay Mathematics Institute prometió un millón de dólares. Si bien puede ser que el problema de factorización se polinomio, pero la hipótesis de Riemann es ni probar ni refutar.
Desechados si el número de sombras?
Dado que no conocemos las leyes por los que pueda encontrar fácilmente los números primos, tal vez mirar de cerca los patrones de números de electores? Matemáticamente hablando, tenemos en cuenta el conjunto de los números naturales, que sea adicional a la serie de intervenciones sencillas
.
La idea es números compuestos muy sencillos. Tómese unos números naturales y multiplicarlos. Por lo tanto, tenemos un número compuesto.
Somos fáciles de encontrar números compuestos infinito, simplemente multiplicando n por 2.

Lo mismo se aplica a la multiplicación por 3.

Seguido de 4, pero aquí no encontramos nuevos números, todos ellos tienen la misma 2n. Seguido 5n, a continuación, 6n, que encontramos el doble de tiempo 2n y 3n. No aumenta el número de números compuestos, sino que nos lleva a creer que el patrón de números compuestos está contenida en el producto simple.
Pero si vamos un poco más allá, encontramos un patrón interesante: el número 6 es el producto de 2 y 3. Esto significa que vamos a tener muchos convenientemente situado justo en la tabla de números compuestos:
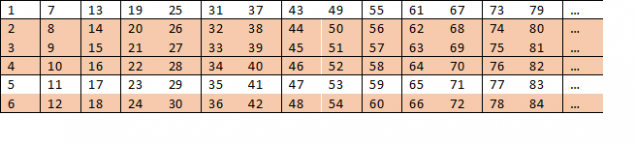
Mirando la tabla, entendemos que en las líneas 2, 3, 4 y 6 nunca puedan ser números primos. Esto significa que la probabilidad de encontrar un número primo no puede exceder 2/6. Nos damos cuenta de que los números, esta probabilidad es aún más pequeño, pero ¿cuánto?
Trate de seguir buscando una estructura adecuada de números compuestos, y para ello, pensar en lo que significa 2x3 = 6? Lo que si tenemos el producto de 2h3h5 una base? Obtenemos la siguiente tabla interesante (por lo que no ocupa mucho espacio, disminuir fuente):
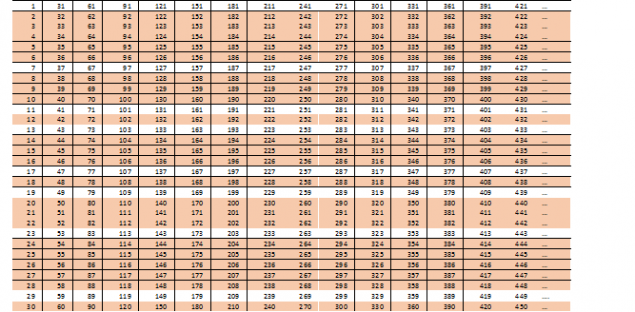
Podemos ver que:
- 15 líneas de la forma 2n,
- 5 líneas de la forma 3n (6n + 5 especies ya incluidas en 2n)
- Y 2 líneas de la forma 5n (10N tres especies ya borrados en número 2n y uno entre las líneas 15N 3n)
no puede contener números primos (que esperábamos esto, ¿verdad?)
Hay sólo ocho filas forman 30n + i, donde i = 1, 7, 11, 13, 17, 19, 23, 29. Si nos fijamos en la simetría de ellos se pueden ver. 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17.
Por lo tanto, como se puede escribir de forma compacta 30n + - i, donde i = 1, 7, 11, 13, 17
Y entendemos que la probabilidad de encontrar un primer número arbitrario no más de 8/30. En 2/30 menos ...
Que es lo siguiente? Lógicamente, en el siguiente cuadro debe ser 2h3h5h7 = 210 líneas. Aún más 210h11 = 2310 entonces 2310h13, y así multiplicaremos consistentemente primos, cada vez más grande y la base más grande "horizontal", que mantendrá su anillamiento.
Parece como si los números primos echaron "sombras" al infinito ellos varios números si se colocan en una fila, respectivamente, de la base, que denotamos por P (i), igual al producto de i primos consecutivos.
Se puede observar que las líneas de tira se extiende entre el primero y el siguiente, que puede contener un simple número está creciendo a una ley muy simple: si las líneas 6, que es 2x3, los números primos pueden estar en la línea 5, si 2h3h5, a continuación, a partir de la fila 7 , lo que es lógico. Así, en una matriz con el número de filas 30 030 (2h3h5h7h11h13) después de la primera línea es el número de compuestos de banda ancha, al número de línea de la próxima 17. Si tomamos la matriz a 9.699.690 filas (2h3h5h7h11h13h17h19), la franja donde los números primos sin estiramiento a la línea 21. Como es típico, debido a la simetría, la parte inferior de la matriz también será de 20 líneas con sólo números compuestos.
La matriz y del hiperrealismo fractales multidimensionales?
¿Pero cuáles son estas obras? 2x3 - un rectángulo con una superficie de 6 2h3h5 - volumen paralelepípedo 30. Y entonces? 2h3h5h7 - giperparallelepiped en 4 dimensiones, con hipervolumen 210? Y entonces? 5 mediciones, 6, ... Infinito?
Basta pensar lo que podría haber imaginado mundo multidimensional en el que los números primos proyectan su sombra en todas las dimensiones ...
Podemos imaginar cuatro o más dimensiones, proyectados sobre un plano o en el espacio tridimensional, por ejemplo, la ampliación de la matriz, como rodar un hipercubo multidimensional con las caras en el borde, y teniendo en cuenta las impresiones resultantes en papel (así como obtener copias de secciones).
Éstos son la faceta inicial:

Pero su escanear ambas caras:

Muy bien, que en todo el hiperplano derecho nosotros sólo números compuestos. Ni siquiera se puede viajar. Usted puede mirar en otra exploración, vista "desde arriba", pero vamos a ir más lejos en una dirección más interesante.
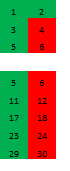
Tratemos ahora de implementar la imagen a la cuarta dimensión, estamos interesados en la dirección de donde se puede encontrar números primos:

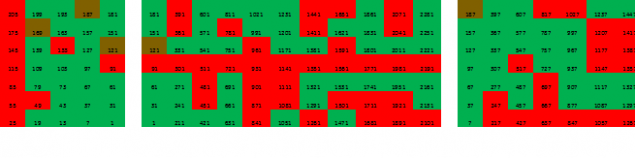
Aquí el color marrón indica el número de la forma mn, que compila las obras de los números del 11 al 19 (el número entero inmediatamente inferior a 210/11). La peculiaridad de estos números es que no están siendo primos no "sombras" de profundidad en la próxima dimensión.
Como podemos ver, el barrido capa media se convierte de nuevo trivial - en adelante no ceba. Pero los giperpallelepipeda bordes exteriores pueden considerarse más. Cada columna de la matriz se descompone en 7H11, obtener 5 de estas matrices para cada una de las tres capas de matriz de 3x5 (que se muestra aquí de barrido de una columna y un fragmento de la matriz para la segunda columna):
Entonces entra en la medición del ejemplo de exploración que no lo haremos, en virtud del artículo sería imprudente. Al final del artículo, se puede ver en algunas ilustraciones. Esperamos que este estudio se despertó un poco su imaginación y viaje en el mundo de difícil y primos que te gustó y parecía servicial.
Conclusión
Además, el autor desea señalar que el estudio continuo de este método. Por ejemplo, las preguntas aparecen en las matrices más grandes obras de las potencias del tercer, cuarto y más de los números que se suman nuevos números primos en las proyecciones de profundidad y volumen como para ensombrecer la siguiente medición, y sigue siendo un inclusiones "puntuales".
Pero quizás lo más interesante es la posibilidad de verificar las estimaciones de la probabilidad de encontrar números primos más y más. Si tenemos en cuenta la matriz, vemos la probabilidad de caídas, empezando por 4/6, y luego a 7.24 (o un promedio de 11/30), a continuación, 36/180 (o 47/210), etc.
Además, el autor tiene un algoritmo de factorización, la optimización es una matriz multidimensional puede acelerar significativamente hacia arriba (pero esto no deja de tener un grado de dificultad exponencial del número de caracteres degradables).
El propio algoritmo se basa en una muy simple.
Tomar dos sucesivos números impares, p y q, de modo que pq cerca de X (redondeo se utiliza para la raíz X de la más grande y más pequeño de los números impares, con la condición de que X no es un cuadrado). Anteriormente, eliminamos la paridad X (divide por 2, siempre y cuando el resultado es aún) para dar el factor 2 ^ K. Además, en el bucle de comprobar la diferencia entre X e pq. Si es cero - el resultado obtenido. Si es mayor que cero, reducimos q en 2. Si es menos de cero, aumentamos p por 2q. El bucle única adición, por lo que el algoritmo es muy rápido (sólo depende de la realización de funciones con BigInteger).
Sin embargo, el autor ha planteado la hipótesis de que el paso de conversión puede incrementarse significativamente sin pérdida de precisión si usamos la multiplicidad base. X es cualquier número entre dos P consecutivo (i) y P (i + 1), donde n (i) - el producto del primer número primo i, por lo que se puede determinar que el número X de las costillas y que es más de cerca y la libertad de p q en cada proyección) y p y q formada de este modo de un rectángulo en un plano de sección giperparallelepipeda expanden.
PD ¿Y qué son la sociedad secreta de los tejedores, preguntará el lector, que empató el título original? El lector puede recordar la película "Se busca" este año promete aún más ... En este telar película hace predicciones, poniendo hilos y nudos ... Mira lo similar que hace que las cadenas de números primos ...
El 30h7 matriz:

Y un trozo de matriz 210h11:
Y esta máquina es controlada nódulos aquí son tarjetas de matriz-perforadas. Matrices 2x3 de digitalización:

Y más, matrices 6x5:

Fuente: habrahabr.ru/post/255527/

El autor ofrece una visión de lo que es un conjunto de números primos, si nos fijamos en su forma geométrica. Esto no es un trabajo profesional, pero un estudio simple, aficionado de algunos patrones interesantes. Por lo tanto, el artículo no será complicada de las matemáticas, y no vamos a subir el fondo de su selva. En general, si usted no está muy familiarizado con los números primos, su estructura y la centenaria investigación en la teoría de números, en este artículo - para usted.

subrayo especialmente para los matemáticos especializados y aquellos lectores que sí se aplica a ellos: el artículo no es un trabajo profesional. Esta es una ilustración de algunas propiedades y patrones de números compuestos, únicamente para la identificación de patrones de énfasis en la estructura a efectos ilustrativos, que luego se pueden expresar analíticamente i>
Probablemente el lector está familiarizado con muchos de los problemas asociados con números primos. Su ubicación en el conjunto de números naturales no es obvia. Números primos grandes es difícil de encontrar, es necesario un gran esfuerzo para revisar una gran cantidad de su simplicidad. Esta dificultad se basa, muchos métodos modernos de la criptografía. Podemos multiplicar fácilmente primos sí de varios valores, pero sabiendo el resultado de encontrar los factores originales - una tarea muy difícil.
Hay muchas maneras de optimizar así de simple clasificación es mucho más rápido, pero incluso si la búsqueda de optimización se acelerará a 10 veces, es suficiente para aumentar el número de decimales a 2 (es decir, 100) para ralentizar la búsqueda en 100 veces.
Esto significa que la complejidad del algoritmo es exponencial, por lo que no importa qué tan rápido o era un superordenador, podemos elegir la longitud de más de estos superordenadores tomó millones de dólares. Es cierto que es necesario aclarar una vez más: encontrar números primos para multiplicar luego se convierte en sólo cada vez más difícil
.
Por cierto, los matemáticos no se encontró ninguna evidencia ni negar que es imposible encontrar un algoritmo de factorización, la complejidad de los cuales no sería dependiente de forma exponencial en la longitud del número. Y probar o refutar que, como algunos creen las matemáticas, se puede obtener, al mismo tiempo, para resolver un problema matemático conocido como la hipótesis de Riemann. Por su prueba Clay Mathematics Institute prometió un millón de dólares. Si bien puede ser que el problema de factorización se polinomio, pero la hipótesis de Riemann es ni probar ni refutar.
Desechados si el número de sombras?
Dado que no conocemos las leyes por los que pueda encontrar fácilmente los números primos, tal vez mirar de cerca los patrones de números de electores? Matemáticamente hablando, tenemos en cuenta el conjunto de los números naturales, que sea adicional a la serie de intervenciones sencillas
.
La idea es números compuestos muy sencillos. Tómese unos números naturales y multiplicarlos. Por lo tanto, tenemos un número compuesto.
Somos fáciles de encontrar números compuestos infinito, simplemente multiplicando n por 2.

Lo mismo se aplica a la multiplicación por 3.

Seguido de 4, pero aquí no encontramos nuevos números, todos ellos tienen la misma 2n. Seguido 5n, a continuación, 6n, que encontramos el doble de tiempo 2n y 3n. No aumenta el número de números compuestos, sino que nos lleva a creer que el patrón de números compuestos está contenida en el producto simple.
Pero si vamos un poco más allá, encontramos un patrón interesante: el número 6 es el producto de 2 y 3. Esto significa que vamos a tener muchos convenientemente situado justo en la tabla de números compuestos:

Mirando la tabla, entendemos que en las líneas 2, 3, 4 y 6 nunca puedan ser números primos. Esto significa que la probabilidad de encontrar un número primo no puede exceder 2/6. Nos damos cuenta de que los números, esta probabilidad es aún más pequeño, pero ¿cuánto?
Trate de seguir buscando una estructura adecuada de números compuestos, y para ello, pensar en lo que significa 2x3 = 6? Lo que si tenemos el producto de 2h3h5 una base? Obtenemos la siguiente tabla interesante (por lo que no ocupa mucho espacio, disminuir fuente):

Podemos ver que:
- 15 líneas de la forma 2n,
- 5 líneas de la forma 3n (6n + 5 especies ya incluidas en 2n)
- Y 2 líneas de la forma 5n (10N tres especies ya borrados en número 2n y uno entre las líneas 15N 3n)
no puede contener números primos (que esperábamos esto, ¿verdad?)
Hay sólo ocho filas forman 30n + i, donde i = 1, 7, 11, 13, 17, 19, 23, 29. Si nos fijamos en la simetría de ellos se pueden ver. 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17.
Por lo tanto, como se puede escribir de forma compacta 30n + - i, donde i = 1, 7, 11, 13, 17
Y entendemos que la probabilidad de encontrar un primer número arbitrario no más de 8/30. En 2/30 menos ...
Que es lo siguiente? Lógicamente, en el siguiente cuadro debe ser 2h3h5h7 = 210 líneas. Aún más 210h11 = 2310 entonces 2310h13, y así multiplicaremos consistentemente primos, cada vez más grande y la base más grande "horizontal", que mantendrá su anillamiento.
Parece como si los números primos echaron "sombras" al infinito ellos varios números si se colocan en una fila, respectivamente, de la base, que denotamos por P (i), igual al producto de i primos consecutivos.
Se puede observar que las líneas de tira se extiende entre el primero y el siguiente, que puede contener un simple número está creciendo a una ley muy simple: si las líneas 6, que es 2x3, los números primos pueden estar en la línea 5, si 2h3h5, a continuación, a partir de la fila 7 , lo que es lógico. Así, en una matriz con el número de filas 30 030 (2h3h5h7h11h13) después de la primera línea es el número de compuestos de banda ancha, al número de línea de la próxima 17. Si tomamos la matriz a 9.699.690 filas (2h3h5h7h11h13h17h19), la franja donde los números primos sin estiramiento a la línea 21. Como es típico, debido a la simetría, la parte inferior de la matriz también será de 20 líneas con sólo números compuestos.
La matriz y del hiperrealismo fractales multidimensionales?
¿Pero cuáles son estas obras? 2x3 - un rectángulo con una superficie de 6 2h3h5 - volumen paralelepípedo 30. Y entonces? 2h3h5h7 - giperparallelepiped en 4 dimensiones, con hipervolumen 210? Y entonces? 5 mediciones, 6, ... Infinito?
Basta pensar lo que podría haber imaginado mundo multidimensional en el que los números primos proyectan su sombra en todas las dimensiones ...
Podemos imaginar cuatro o más dimensiones, proyectados sobre un plano o en el espacio tridimensional, por ejemplo, la ampliación de la matriz, como rodar un hipercubo multidimensional con las caras en el borde, y teniendo en cuenta las impresiones resultantes en papel (así como obtener copias de secciones).
Éstos son la faceta inicial:

Pero su escanear ambas caras:

Muy bien, que en todo el hiperplano derecho nosotros sólo números compuestos. Ni siquiera se puede viajar. Usted puede mirar en otra exploración, vista "desde arriba", pero vamos a ir más lejos en una dirección más interesante.

Tratemos ahora de implementar la imagen a la cuarta dimensión, estamos interesados en la dirección de donde se puede encontrar números primos:

Aquí el color marrón indica el número de la forma mn, que compila las obras de los números del 11 al 19 (el número entero inmediatamente inferior a 210/11). La peculiaridad de estos números es que no están siendo primos no "sombras" de profundidad en la próxima dimensión.
Como podemos ver, el barrido capa media se convierte de nuevo trivial - en adelante no ceba. Pero los giperpallelepipeda bordes exteriores pueden considerarse más. Cada columna de la matriz se descompone en 7H11, obtener 5 de estas matrices para cada una de las tres capas de matriz de 3x5 (que se muestra aquí de barrido de una columna y un fragmento de la matriz para la segunda columna):

Entonces entra en la medición del ejemplo de exploración que no lo haremos, en virtud del artículo sería imprudente. Al final del artículo, se puede ver en algunas ilustraciones. Esperamos que este estudio se despertó un poco su imaginación y viaje en el mundo de difícil y primos que te gustó y parecía servicial.
Conclusión
Además, el autor desea señalar que el estudio continuo de este método. Por ejemplo, las preguntas aparecen en las matrices más grandes obras de las potencias del tercer, cuarto y más de los números que se suman nuevos números primos en las proyecciones de profundidad y volumen como para ensombrecer la siguiente medición, y sigue siendo un inclusiones "puntuales".
Pero quizás lo más interesante es la posibilidad de verificar las estimaciones de la probabilidad de encontrar números primos más y más. Si tenemos en cuenta la matriz, vemos la probabilidad de caídas, empezando por 4/6, y luego a 7.24 (o un promedio de 11/30), a continuación, 36/180 (o 47/210), etc.
Además, el autor tiene un algoritmo de factorización, la optimización es una matriz multidimensional puede acelerar significativamente hacia arriba (pero esto no deja de tener un grado de dificultad exponencial del número de caracteres degradables).
El propio algoritmo se basa en una muy simple.
Tomar dos sucesivos números impares, p y q, de modo que pq cerca de X (redondeo se utiliza para la raíz X de la más grande y más pequeño de los números impares, con la condición de que X no es un cuadrado). Anteriormente, eliminamos la paridad X (divide por 2, siempre y cuando el resultado es aún) para dar el factor 2 ^ K. Además, en el bucle de comprobar la diferencia entre X e pq. Si es cero - el resultado obtenido. Si es mayor que cero, reducimos q en 2. Si es menos de cero, aumentamos p por 2q. El bucle única adición, por lo que el algoritmo es muy rápido (sólo depende de la realización de funciones con BigInteger).
Sin embargo, el autor ha planteado la hipótesis de que el paso de conversión puede incrementarse significativamente sin pérdida de precisión si usamos la multiplicidad base. X es cualquier número entre dos P consecutivo (i) y P (i + 1), donde n (i) - el producto del primer número primo i, por lo que se puede determinar que el número X de las costillas y que es más de cerca y la libertad de p q en cada proyección) y p y q formada de este modo de un rectángulo en un plano de sección giperparallelepipeda expanden.
PD ¿Y qué son la sociedad secreta de los tejedores, preguntará el lector, que empató el título original? El lector puede recordar la película "Se busca" este año promete aún más ... En este telar película hace predicciones, poniendo hilos y nudos ... Mira lo similar que hace que las cadenas de números primos ...
El 30h7 matriz:

Y un trozo de matriz 210h11:

Y esta máquina es controlada nódulos aquí son tarjetas de matriz-perforadas. Matrices 2x3 de digitalización:

Y más, matrices 6x5:

Fuente: habrahabr.ru/post/255527/
Sobrepeso salva de demencia adquirida
Canal de televisión francés fue hackeado después de las pegatinas fondo personal de entrevista con contraseñas