1647
Диффікулт прем'єрних чисел: секрети таємного суспільства
Неускладнені номери

Автор статті пропонує погляд на те, які набори прем’єрних чисел, якщо ви подивитеся на них геометрично. Це не професійна робота, але простий, любительське дослідження деяких цікавих шаблонів. Таким чином, стаття не буде складною математикою, і ми не будемо глибоко переходити в її дикі. В цілому, якщо ви не дуже знайомі з першоджереломи, їх структура та вікові дослідження в теорії чисел, ця стаття для вас.

Особливо для кваліфікованих математиків і тих читачів, які вважають себе серед них: стаття не професійна робота. Це ілюстрація деяких властивостей і закономірностей композитних чисел, виключно заради чіткості і ідентифікації акценту на закономірностях структури, які в подальшому можуть бути виражені аналітично.
Читач, ймовірно, знає багато проблем з першоджерелом. Місцезнаходження в комплекті натуральних чисел не очевидна. Більшість основних чисел важко знайти, це займе багато зусиль, щоб перевірити велику кількість для простоти. Багато сучасних методів криптографії базуються на цій складності. Ми можемо легко перемножувати такі багатодітки, але знаючи результат, знайти оригінальні мультиплікатори є дуже складним завданням.
Існує багато способів оптимізації, які набагато швидше, ніж брутна сила, але навіть якщо оптимізація прискорює пошук по 10 разів, тільки збільшити кількість на 2 десяткових місця (тобто 100 разів) для уповільнення пошуку по 100 разів.
Це означає, що складність алгоритму є доцільним, і тому неважливо, наскільки швидко суперкомп'ютер, ми можемо відповідати довжині кількості навіть довше, щоб такі суперкомп'ютери вимагають мільярдів. Тим не менш, варто з'ясувати ще раз: знайти першоджерело для багатозастосувань одночасно стає більш складним.
До речі, математики не знайшли ніяких доказів, які не можна знайти алгоритм факторизації, складність яких не є доцільним залежним від довжини числа. І пров'язуючи або відхиляючи це, деякі математики вірять, це може бути можливо вирішити математичну проблему, відома як гіпотеза Рієман. За його доказом, Інститут Клей Математичний обіцяє мільйон доларів. Незважаючи на те, що проблема факторизації може бути поліноміальною, це не доведеться, а не розпроваджувати гіпотезу Ріємана.
Чи є цифри відтінені тіні?
Оскільки ми не знаємо закони, за якими можна знайти основні числа, можливо, ми повинні уважно дивитися закони композитних чисел? Математично кажучи, розглянемо набір натуральних чисел, крім набору прем'єрів.
Ідея з'єднання дуже проста. Візьміть кілька натуральних чисел і помножте їх. Так ми отримуємо композитний номер.
Ми можемо легко знайти нескінченність сполук, просто помножуючи n на 2.

Те ж саме йде для мультиплікації на 3.
 р.
р.
Далі йде 4, але тут ми не знайдемо нових чисел, вони всі рівні до 2n. Далі йде 5n, потім 6n, які ми знайшли двічі, як 2n і 3n одночасно. Це не збільшує кількість з'єднань, але говорить про те, що регулярність з'єднання чисел лежить в продукті основних чисел.
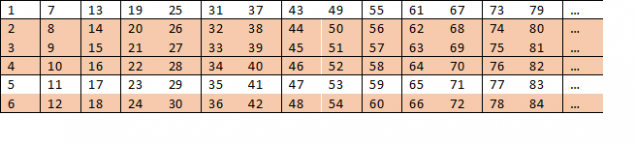
Але якщо ми йдемо трохи далі, ми знайдемо цікавий візерунок: 6 - продукт 2 і 3. Це означає, що у нас є одночасно багато зручно розташованих в таблиці композитних чисел:
 р.
р.
Дивлячись на таблицю, ми усвідомлюємо, що рядки 2, 3, 4 і 6 ніколи не мають вихідних номерів. Це означає, що ймовірність пошуку першого числа не може перевищувати 2/6. Ми розуміємо, що номери є менш ймовірними, але скільки?
Давайте продовжуємо шукати зручну структуру з'єднань, і для цього подумайте про те, що означає 2х3=6? Що, якщо ми взяли шматок 2x3x5 як основа? Ми отримуємо наступний цікавий стіл (наприклад, він не займає багато місця, зменшуємо шрифт):
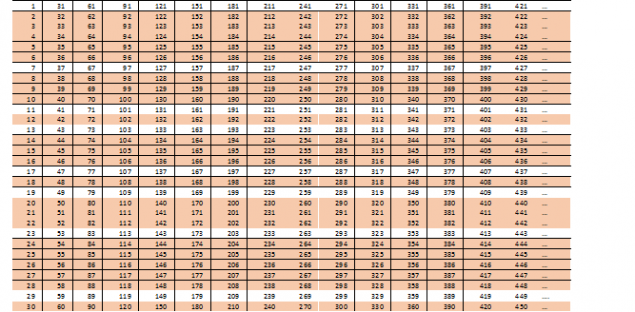
Ми бачимо:
- 15 ліній типу 2н,
5 ліній 3n (плюс 5 6n вже рахується в 2n)
- і 2 лінії форми 5n (три більше типів 10n вже перекреслилися в числах 2n і 15n серед ліній 3n)
Вони не повинні бути простими (що ми очікуємо, прямо?)
Тільки вісім ліній форми 30n + я залишатися, де i = 1, 7, 11, 13, 17, 23, 29. Якщо ви уважно дивитесь, ви можете побачити симетрію. 1+29=7+23=11+19=13+17.
Таким чином, це може бути письмово, як 30n +- i, де i = 1, 7, 11, 13, 17.
І ми розуміємо, що ймовірність пошуку довільного прем'єра не більше 8/30. Це було 2/30 менше...
Що далі? Після логіки, наступний стіл повинен бути 2x3x5x7=210 ліній. Навіть далі, 210 x 11 = 2310, потім 2310 x 13, і тому ми послідовно розмножуємо першоджерело, отримуємо більшу і більшу базу «лінійного ковпача», яка збереже свою смугу.
Виглядає, як якщо в рядах, які кладуть «шадови» в нескінченність чисел, якщо вони розташовуються в серії відповідно до бази числа, ми позначаємо її P(i), що дорівнює послідовному продукту i прем'єри.
Ви можете бачити, що смуга ліній, що лежать між першою і наступною, де можуть міститися основні числа, виростає відповідно до дуже простого закону: якщо ряди 6, тобто 2 × 3, то основні числа можуть бути в лінії 5, якщо 2 × 3 × 5, то починаючи з лінії 7, який логічний. Таким чином, в матриці з числом рядів 30 030 (2x3x5x7x11x13) після першої лінії буде широка смуга композитних чисел, до ряду за номером 17. І якщо беремо матрицю 9,699,690 ліній (2x3x5x7x11x13x17x19), то смуга, де не простягається на лінії 21. Характерно, через симетрію, дно матриці також буде мати 20 ліній з виключно композитними числами.
Багатовимірні матриці та гіперреалістичні фрактали?
Але які ці роботи? 2x3 - прямокутник з зоною 6. 2x3x5 - паралелеп, об'єм 30. А потім? 2x3x5x7 - гіперпаралелепіпед в 4 розмірах, з гіперобом 210? А потім? 5 розмірів, 6, ... нескінченність?
Уявіть багатовимірний світ, в якому основні номери виливають тіні у всіх розмірах.
Ми можемо уявити чотири або більше розмірів, пройшовши їх на площину або в об'ємний простір, наприклад, прокладаючи матрицю, так як при прокаті багатовимірного гіперкуму з обличчя до обличчя і з урахуванням друку, отриманих на папері (як і отримання транссекційних відбитків).
Ось стартова лінія:

І ось її ковтати по обидва боки:

Це дуже важливо, щоб у всьому правому гіперплані ми маємо виключно композитні номери. Ми не повинні подорожувати. Ви можете подивитися на інший сканування, вид зверху, але потім ми йдемо в більш цікавий напрямок.
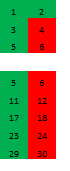
Тепер намагайтеся розширити картину в четвертий розмір, в напрямку ми зацікавлені, де можна знайти основні номери:

Тут коричневий колір вказує цифри форми mn, які складаються з продуктів чисел від 11 до 19 (близьке ціле, менше 210/11). Особливість цих чисел полягає в тому, що вони самі не є першочерговими числами, які не пролиті тіні глибоко в наступному вимірі.
Як бачимо, середній шар ковтки знову стає тривіальним – тут немає першоджерело. Але зовнішні краї гіперпаллепіпеда можна вважати далі. Кожен стовпчик декомпонований в матриці 7x11, ми отримуємо 5 таких матриць для кожного з трьох шарів матриці 3x5 (це сканування одного стовпчика і фрагмент матриці для другого стовпця):
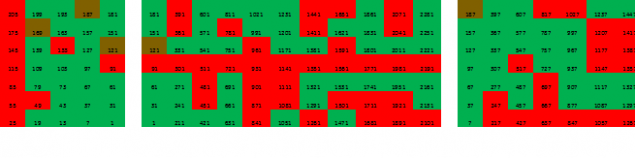
Ми не будемо йти далі в вимірювання на прикладі сканування, в рамках статті це буде незворотно. В кінці статті ви можете переглянути деякі більш ілюстрації. Я сподіваюся, що це дослідження трохи пробудив свою фантазію, і подорож в світ складних і першокласних номерів, які вам сподобалося і здавалося б корисним.
Висновок
Крім того, автор бажає відзначити, що він продовжує вивчати цей метод. Наприклад, питання зовнішнього вигляду в більших матрицях виробів третього, четвертого і подальшого ступенів чисел, які додають нові першоджерело в глибоких і об'ємних проекціях, як лиття тіней в наступних розмірах, так і решта «точкових» міжпорошків.
Але, можливо, найцікавіше, є можливість уточнення ймовірності пошуку першоджерело і далі. Якщо ми подивимося на матриці, ми бачимо, як ймовірність спадає від 4/6, то до 7/24 (або 11/30 середній), то 36/180 (або 47/210), і так далі.
Крім того, автор має факторизація алгоритму, оптимізація якого в багатовимірній матриці може істотно прискорити його (але не перестає мати доцільний ступінь складності від кількості ознак декомплаєного числа).
Сам алгоритм в основному дуже простий.
Візьміть дві непарні числа, р і q, такі, що Pq є близьким до X (закруглення кореня від X до більших і менших непарних чисел використовується, за умови, що X не є квадратом). Попередньо ми усуваємо парність X (відповіли на 2 до тих пір, як результат навіть), отримуємо фактор 2^K. Далі в циклі перевірте різницю між X і Pq. Якщо це нуль, результат виходить. Якщо це більше, ніж нуль, ми зменшуємо q на 2. Якщо менше нуля, збільшити р по 2к. Цикл використовує тільки додаток, тому алгоритм досить швидко (в залежності тільки від виконання функцій роботи з BigInteger).
Тим не менш, автор має гіпотезу, що крок рекалькуляції може бути значно збільшений без втрати точності, якщо ви використовуєте базу мультиплікації. Кожна кількість X є між двома послідовними P(i) і P(i+1), де P(i) є продуктом перших і прем'єрних чисел, тому можна визначити, який з країв кількість X ближче і який діапазон свободи y p і q в кожному з проекцій) і тим самим формувати p і q прямокутник з однієї площини, щоб розширити переріз гіперпаралелепіпеда.
П.С. І що це потрібно робити з секретним суспільством вівчарів, читач запитатиме, хто привертався до оригінального заголовка? Можливо, читач пам'ятає фільм "Ефективно небезпечний" Цього року вони обіцяють продовжити ... У цій плівці ткацький верстат виготовляє прогнози, укладання ниток і вузликів. Дивись як аналогічно рядки з першоджерело.
У матриці 30х7:

І шматок матриці 210х11:
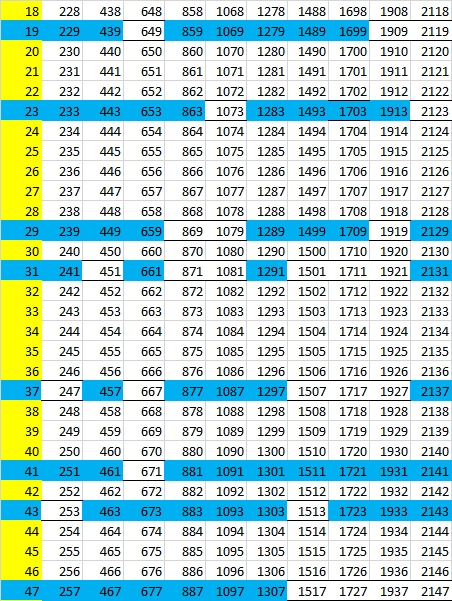
І вузли в цій машині контролюються цими матриками для пучок. 2х3 матриць:

І більше, 6x5 матриць:

Джерело: habrahabr.ru/post/255527/

Автор статті пропонує погляд на те, які набори прем’єрних чисел, якщо ви подивитеся на них геометрично. Це не професійна робота, але простий, любительське дослідження деяких цікавих шаблонів. Таким чином, стаття не буде складною математикою, і ми не будемо глибоко переходити в її дикі. В цілому, якщо ви не дуже знайомі з першоджереломи, їх структура та вікові дослідження в теорії чисел, ця стаття для вас.

Особливо для кваліфікованих математиків і тих читачів, які вважають себе серед них: стаття не професійна робота. Це ілюстрація деяких властивостей і закономірностей композитних чисел, виключно заради чіткості і ідентифікації акценту на закономірностях структури, які в подальшому можуть бути виражені аналітично.
Читач, ймовірно, знає багато проблем з першоджерелом. Місцезнаходження в комплекті натуральних чисел не очевидна. Більшість основних чисел важко знайти, це займе багато зусиль, щоб перевірити велику кількість для простоти. Багато сучасних методів криптографії базуються на цій складності. Ми можемо легко перемножувати такі багатодітки, але знаючи результат, знайти оригінальні мультиплікатори є дуже складним завданням.
Існує багато способів оптимізації, які набагато швидше, ніж брутна сила, але навіть якщо оптимізація прискорює пошук по 10 разів, тільки збільшити кількість на 2 десяткових місця (тобто 100 разів) для уповільнення пошуку по 100 разів.
Це означає, що складність алгоритму є доцільним, і тому неважливо, наскільки швидко суперкомп'ютер, ми можемо відповідати довжині кількості навіть довше, щоб такі суперкомп'ютери вимагають мільярдів. Тим не менш, варто з'ясувати ще раз: знайти першоджерело для багатозастосувань одночасно стає більш складним.
До речі, математики не знайшли ніяких доказів, які не можна знайти алгоритм факторизації, складність яких не є доцільним залежним від довжини числа. І пров'язуючи або відхиляючи це, деякі математики вірять, це може бути можливо вирішити математичну проблему, відома як гіпотеза Рієман. За його доказом, Інститут Клей Математичний обіцяє мільйон доларів. Незважаючи на те, що проблема факторизації може бути поліноміальною, це не доведеться, а не розпроваджувати гіпотезу Ріємана.
Чи є цифри відтінені тіні?
Оскільки ми не знаємо закони, за якими можна знайти основні числа, можливо, ми повинні уважно дивитися закони композитних чисел? Математично кажучи, розглянемо набір натуральних чисел, крім набору прем'єрів.
Ідея з'єднання дуже проста. Візьміть кілька натуральних чисел і помножте їх. Так ми отримуємо композитний номер.
Ми можемо легко знайти нескінченність сполук, просто помножуючи n на 2.

Те ж саме йде для мультиплікації на 3.
 р.
р.Далі йде 4, але тут ми не знайдемо нових чисел, вони всі рівні до 2n. Далі йде 5n, потім 6n, які ми знайшли двічі, як 2n і 3n одночасно. Це не збільшує кількість з'єднань, але говорить про те, що регулярність з'єднання чисел лежить в продукті основних чисел.
Але якщо ми йдемо трохи далі, ми знайдемо цікавий візерунок: 6 - продукт 2 і 3. Це означає, що у нас є одночасно багато зручно розташованих в таблиці композитних чисел:
 р.
р.Дивлячись на таблицю, ми усвідомлюємо, що рядки 2, 3, 4 і 6 ніколи не мають вихідних номерів. Це означає, що ймовірність пошуку першого числа не може перевищувати 2/6. Ми розуміємо, що номери є менш ймовірними, але скільки?
Давайте продовжуємо шукати зручну структуру з'єднань, і для цього подумайте про те, що означає 2х3=6? Що, якщо ми взяли шматок 2x3x5 як основа? Ми отримуємо наступний цікавий стіл (наприклад, він не займає багато місця, зменшуємо шрифт):

Ми бачимо:
- 15 ліній типу 2н,
5 ліній 3n (плюс 5 6n вже рахується в 2n)
- і 2 лінії форми 5n (три більше типів 10n вже перекреслилися в числах 2n і 15n серед ліній 3n)
Вони не повинні бути простими (що ми очікуємо, прямо?)
Тільки вісім ліній форми 30n + я залишатися, де i = 1, 7, 11, 13, 17, 23, 29. Якщо ви уважно дивитесь, ви можете побачити симетрію. 1+29=7+23=11+19=13+17.
Таким чином, це може бути письмово, як 30n +- i, де i = 1, 7, 11, 13, 17.
І ми розуміємо, що ймовірність пошуку довільного прем'єра не більше 8/30. Це було 2/30 менше...
Що далі? Після логіки, наступний стіл повинен бути 2x3x5x7=210 ліній. Навіть далі, 210 x 11 = 2310, потім 2310 x 13, і тому ми послідовно розмножуємо першоджерело, отримуємо більшу і більшу базу «лінійного ковпача», яка збереже свою смугу.
Виглядає, як якщо в рядах, які кладуть «шадови» в нескінченність чисел, якщо вони розташовуються в серії відповідно до бази числа, ми позначаємо її P(i), що дорівнює послідовному продукту i прем'єри.
Ви можете бачити, що смуга ліній, що лежать між першою і наступною, де можуть міститися основні числа, виростає відповідно до дуже простого закону: якщо ряди 6, тобто 2 × 3, то основні числа можуть бути в лінії 5, якщо 2 × 3 × 5, то починаючи з лінії 7, який логічний. Таким чином, в матриці з числом рядів 30 030 (2x3x5x7x11x13) після першої лінії буде широка смуга композитних чисел, до ряду за номером 17. І якщо беремо матрицю 9,699,690 ліній (2x3x5x7x11x13x17x19), то смуга, де не простягається на лінії 21. Характерно, через симетрію, дно матриці також буде мати 20 ліній з виключно композитними числами.
Багатовимірні матриці та гіперреалістичні фрактали?
Але які ці роботи? 2x3 - прямокутник з зоною 6. 2x3x5 - паралелеп, об'єм 30. А потім? 2x3x5x7 - гіперпаралелепіпед в 4 розмірах, з гіперобом 210? А потім? 5 розмірів, 6, ... нескінченність?
Уявіть багатовимірний світ, в якому основні номери виливають тіні у всіх розмірах.
Ми можемо уявити чотири або більше розмірів, пройшовши їх на площину або в об'ємний простір, наприклад, прокладаючи матрицю, так як при прокаті багатовимірного гіперкуму з обличчя до обличчя і з урахуванням друку, отриманих на папері (як і отримання транссекційних відбитків).
Ось стартова лінія:

І ось її ковтати по обидва боки:

Це дуже важливо, щоб у всьому правому гіперплані ми маємо виключно композитні номери. Ми не повинні подорожувати. Ви можете подивитися на інший сканування, вид зверху, але потім ми йдемо в більш цікавий напрямок.

Тепер намагайтеся розширити картину в четвертий розмір, в напрямку ми зацікавлені, де можна знайти основні номери:

Тут коричневий колір вказує цифри форми mn, які складаються з продуктів чисел від 11 до 19 (близьке ціле, менше 210/11). Особливість цих чисел полягає в тому, що вони самі не є першочерговими числами, які не пролиті тіні глибоко в наступному вимірі.
Як бачимо, середній шар ковтки знову стає тривіальним – тут немає першоджерело. Але зовнішні краї гіперпаллепіпеда можна вважати далі. Кожен стовпчик декомпонований в матриці 7x11, ми отримуємо 5 таких матриць для кожного з трьох шарів матриці 3x5 (це сканування одного стовпчика і фрагмент матриці для другого стовпця):

Ми не будемо йти далі в вимірювання на прикладі сканування, в рамках статті це буде незворотно. В кінці статті ви можете переглянути деякі більш ілюстрації. Я сподіваюся, що це дослідження трохи пробудив свою фантазію, і подорож в світ складних і першокласних номерів, які вам сподобалося і здавалося б корисним.
Висновок
Крім того, автор бажає відзначити, що він продовжує вивчати цей метод. Наприклад, питання зовнішнього вигляду в більших матрицях виробів третього, четвертого і подальшого ступенів чисел, які додають нові першоджерело в глибоких і об'ємних проекціях, як лиття тіней в наступних розмірах, так і решта «точкових» міжпорошків.
Але, можливо, найцікавіше, є можливість уточнення ймовірності пошуку першоджерело і далі. Якщо ми подивимося на матриці, ми бачимо, як ймовірність спадає від 4/6, то до 7/24 (або 11/30 середній), то 36/180 (або 47/210), і так далі.
Крім того, автор має факторизація алгоритму, оптимізація якого в багатовимірній матриці може істотно прискорити його (але не перестає мати доцільний ступінь складності від кількості ознак декомплаєного числа).
Сам алгоритм в основному дуже простий.
Візьміть дві непарні числа, р і q, такі, що Pq є близьким до X (закруглення кореня від X до більших і менших непарних чисел використовується, за умови, що X не є квадратом). Попередньо ми усуваємо парність X (відповіли на 2 до тих пір, як результат навіть), отримуємо фактор 2^K. Далі в циклі перевірте різницю між X і Pq. Якщо це нуль, результат виходить. Якщо це більше, ніж нуль, ми зменшуємо q на 2. Якщо менше нуля, збільшити р по 2к. Цикл використовує тільки додаток, тому алгоритм досить швидко (в залежності тільки від виконання функцій роботи з BigInteger).
Тим не менш, автор має гіпотезу, що крок рекалькуляції може бути значно збільшений без втрати точності, якщо ви використовуєте базу мультиплікації. Кожна кількість X є між двома послідовними P(i) і P(i+1), де P(i) є продуктом перших і прем'єрних чисел, тому можна визначити, який з країв кількість X ближче і який діапазон свободи y p і q в кожному з проекцій) і тим самим формувати p і q прямокутник з однієї площини, щоб розширити переріз гіперпаралелепіпеда.
П.С. І що це потрібно робити з секретним суспільством вівчарів, читач запитатиме, хто привертався до оригінального заголовка? Можливо, читач пам'ятає фільм "Ефективно небезпечний" Цього року вони обіцяють продовжити ... У цій плівці ткацький верстат виготовляє прогнози, укладання ниток і вузликів. Дивись як аналогічно рядки з першоджерело.
У матриці 30х7:

І шматок матриці 210х11:

І вузли в цій машині контролюються цими матриками для пучок. 2х3 матриць:

І більше, 6x5 матриць:

Джерело: habrahabr.ru/post/255527/
Надмірна вага економить від придбаної дементії
Французький канал зламати після інтерв'ю співробітника посеред пароля наклейки