804
0.2
2014-12-29
О диагонали квадрата
Введение в оборот комплексных чисел было далеко не первой революцией в понимании человеком природы числа. За две тысячи лет до этого мощнейшее потрясение испытал мир древнегреческой математики.
Неприятности у пифагорейцев начались далеко не сразу. Основанная Пифагором научная школа в итоге кончила плохо, но сегодняшний рассказ не о том бодром погроме, который был учинен над пифагорейцами благодарным за просвещение народом, а в большей степени о духовных перипетиях.
Термин «научная школа» по отношению к организации, основанной Пифагором, является эдаким эвфемизмом. Здраво взглянув на ее структуру и применяемые технологии, пифагореизм следует смело отнести к тоталитарным культам, что было вполне в духе времени (впрочем, это всегда в духе времени, вечная классика). Наличествовало и разделение на степени посвящения, и сложная система ритуалов с запретами (например, общеизвестные, вроде «не есть бобов» или «не откусывать от целой булки»), и сложное философское вероучение. Привет Рону Хаббарду сотоварищи. Ничто не ново под Луной.
В целом, при жизни Пифагора его «школа» была солидным предприятием, к тому же обладающим значительным и все время растущим политическим влиянием.
Вообще, философия Пифагора оказала значительное влияние на западную культуру (и на нас в том числе). Многие идеи нашли свое развитие в классической греческой философии, а уже про теорему Пифагора знают вообще все. Выражение «гармония сфер», кстати, также восходит к пифагорейцам.
Одним из существенных элементов их философии была идея, что любое число можно представить как отношение двух целых чисел, то бишь в виде простой дроби. В этом они, в том числе, видели совершенство природы числа. Больше того, это представлялось вполне очевидным. В современной математике такие числа называются рациональными, а их множество обозначается знаком . Сделайте теперь паузу на несколько секунд, задумайтесь, откуда вообще следует, что это не так? Можете ли вы привести аргумент, который был бы достаточно убедителен для древнего грека? Ну или, хотя бы, достаточно убедителен для себя, лично?
В общем, мир чисел был прост, изящен, и все были довольны. Источником возникших неприятностей, неожиданно, стала уже помянутая теорема, носящая имя Пифагора: одно из важнейших, дошедших до нас, его достижений. К сожалению, доказательство самого Пифагора нам неизвестно. Самое старое из дошедших до нас — приведено в «Началах» Евклида и датируется 3 в. д.н.э. Напомню, сам Пифагор жил в 6 в. д.н.э.
Фрагмент из Vatican Manuscript Number 190, датируемого 10 в. н.э. (целиком здесь):
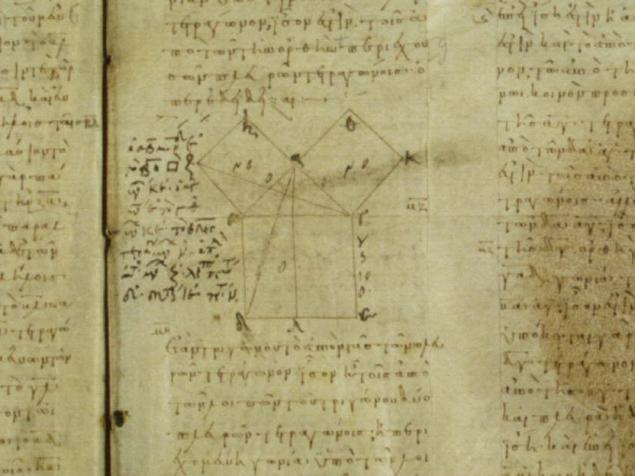
Доказательство Евклида далеко не самое простое. Есть основания считать, что он знал путь и попроще, но из методических соображений привел именно этот вариант, демонстрирующий, помимо собственно теоремы Пифагора, и некоторые другие интересные идеи.
Однако, вернемся к пифагорейцам.
Вот представьте себе простейшую вещь: квадрат со сторонами единичной длины. Если обозначить длину его диагонали, то по теореме Пифагора получим:
и, соответственно:
Само-то по себе это еще не проблема. С точки зрения пифагорейцев, дальше просто нужно было найти целые числа и, такие что
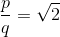
Вот на этом-то «простом» моменте все и застопорилось. Причем наглухо. Стопор сей продолжался до тех пор, пока один умник (как утверждают, Гиппас из Метапонта, тоже пифагореец), не доказал, внезапно, что таких чисел не существует. Все зло от шибко умных идет, как известно. По легенде, это научное достижение столь потрясло коллег, что, в ознаменование признания научных заслуг, Гиппаса не медля вышвырнули за борт корабля, на котором он в момент своего математического озарения плыл. А вот нечего было гадить уважаемым людям, подрывать основы столь любовно выпестованной и весьма доходной философской системы.
Ныне, числа не представимые в виде отношения двух целых, называются иррациональными.
Некоторое время пифагорейцы даже держали факт иррациональности в секрете. Однако, шила в мешке не утаишь, и правда довольно быстро (по историческим меркам) нашла путь наружу.
Доказать иррациональность совсем не сложно.
Пусть существуют такие, что
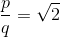
Более того, будем считать, что хотя бы одно из чисел — нечетно. Если это не так, числитель и знаменатель дроби всегда можно сократить на 2 (нужное количество раз).
Тогда получим:
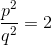
отсюда:
Таким образом, — четное число. Но тогда и — четное.
По условию нечетности хотя бы одного из чисел, получим, что — нечетно.
В силу четности, можно записать
,
где — некоторое целое.
Но тогда:
отсюда
Но это означает, что — четно, а значит четно и. Противоречие.
Число невозможно представить в виде отношения двух целых чисел.
Остается добавить, что — это вовсе не какой-то странный уродец. Можно показать, что иррациональных чисел больше, чем рациональных, принципиально больше. Кстати, отношение больше-меньше в мире бесконечных множеств само бывает весьма контритуитивным. Но это уже другая история.
PS. Пользуясь случаем, поздравляю хабровчан с наступающими. Удачи в новом году!
Источник: habrahabr.ru/post/246963/
Неприятности у пифагорейцев начались далеко не сразу. Основанная Пифагором научная школа в итоге кончила плохо, но сегодняшний рассказ не о том бодром погроме, который был учинен над пифагорейцами благодарным за просвещение народом, а в большей степени о духовных перипетиях.
Термин «научная школа» по отношению к организации, основанной Пифагором, является эдаким эвфемизмом. Здраво взглянув на ее структуру и применяемые технологии, пифагореизм следует смело отнести к тоталитарным культам, что было вполне в духе времени (впрочем, это всегда в духе времени, вечная классика). Наличествовало и разделение на степени посвящения, и сложная система ритуалов с запретами (например, общеизвестные, вроде «не есть бобов» или «не откусывать от целой булки»), и сложное философское вероучение. Привет Рону Хаббарду сотоварищи. Ничто не ново под Луной.
В целом, при жизни Пифагора его «школа» была солидным предприятием, к тому же обладающим значительным и все время растущим политическим влиянием.
Вообще, философия Пифагора оказала значительное влияние на западную культуру (и на нас в том числе). Многие идеи нашли свое развитие в классической греческой философии, а уже про теорему Пифагора знают вообще все. Выражение «гармония сфер», кстати, также восходит к пифагорейцам.
Одним из существенных элементов их философии была идея, что любое число можно представить как отношение двух целых чисел, то бишь в виде простой дроби. В этом они, в том числе, видели совершенство природы числа. Больше того, это представлялось вполне очевидным. В современной математике такие числа называются рациональными, а их множество обозначается знаком . Сделайте теперь паузу на несколько секунд, задумайтесь, откуда вообще следует, что это не так? Можете ли вы привести аргумент, который был бы достаточно убедителен для древнего грека? Ну или, хотя бы, достаточно убедителен для себя, лично?
В общем, мир чисел был прост, изящен, и все были довольны. Источником возникших неприятностей, неожиданно, стала уже помянутая теорема, носящая имя Пифагора: одно из важнейших, дошедших до нас, его достижений. К сожалению, доказательство самого Пифагора нам неизвестно. Самое старое из дошедших до нас — приведено в «Началах» Евклида и датируется 3 в. д.н.э. Напомню, сам Пифагор жил в 6 в. д.н.э.
Фрагмент из Vatican Manuscript Number 190, датируемого 10 в. н.э. (целиком здесь):

Доказательство Евклида далеко не самое простое. Есть основания считать, что он знал путь и попроще, но из методических соображений привел именно этот вариант, демонстрирующий, помимо собственно теоремы Пифагора, и некоторые другие интересные идеи.
Однако, вернемся к пифагорейцам.
Вот представьте себе простейшую вещь: квадрат со сторонами единичной длины. Если обозначить длину его диагонали, то по теореме Пифагора получим:
и, соответственно:
Само-то по себе это еще не проблема. С точки зрения пифагорейцев, дальше просто нужно было найти целые числа и, такие что
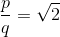
Вот на этом-то «простом» моменте все и застопорилось. Причем наглухо. Стопор сей продолжался до тех пор, пока один умник (как утверждают, Гиппас из Метапонта, тоже пифагореец), не доказал, внезапно, что таких чисел не существует. Все зло от шибко умных идет, как известно. По легенде, это научное достижение столь потрясло коллег, что, в ознаменование признания научных заслуг, Гиппаса не медля вышвырнули за борт корабля, на котором он в момент своего математического озарения плыл. А вот нечего было гадить уважаемым людям, подрывать основы столь любовно выпестованной и весьма доходной философской системы.
Ныне, числа не представимые в виде отношения двух целых, называются иррациональными.
Некоторое время пифагорейцы даже держали факт иррациональности в секрете. Однако, шила в мешке не утаишь, и правда довольно быстро (по историческим меркам) нашла путь наружу.
Доказать иррациональность совсем не сложно.
Пусть существуют такие, что
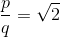
Более того, будем считать, что хотя бы одно из чисел — нечетно. Если это не так, числитель и знаменатель дроби всегда можно сократить на 2 (нужное количество раз).
Тогда получим:
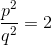
отсюда:
Таким образом, — четное число. Но тогда и — четное.
По условию нечетности хотя бы одного из чисел, получим, что — нечетно.
В силу четности, можно записать
,
где — некоторое целое.
Но тогда:
отсюда
Но это означает, что — четно, а значит четно и. Противоречие.
Число невозможно представить в виде отношения двух целых чисел.
Остается добавить, что — это вовсе не какой-то странный уродец. Можно показать, что иррациональных чисел больше, чем рациональных, принципиально больше. Кстати, отношение больше-меньше в мире бесконечных множеств само бывает весьма контритуитивным. Но это уже другая история.
PS. Пользуясь случаем, поздравляю хабровчан с наступающими. Удачи в новом году!
Источник: habrahabr.ru/post/246963/
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.
Термобарьеры, надгробные камни и прочие прелести печатных плат
Когда технологии опережают потребности: как думали о развитии ИТ в 1985 году