1009
0.3
2016-09-21
Математика с нуля: чем интересно число 0?
Ноль — это, пожалуй, первое в нашей жизни загадочное число. Мы много слышали, например, о чудесах числа Пи, но мало кто имеет с ним дело в повседневной жизни. Не говоря уже о комплексных числах. А вот с нулём мы сталкиваемся повсюду: даже на клавиатуре обозначающая его цифра завершает ряд.
Но любой понимает, что с этим числом не всё в порядке. В детстве, когда мы ещё думали, что арифметика нужна только для счёта, нам объясняли, что ноль — это отсутствие. И это было странно.
Если у меня ноль конфет, считать вообще нечего — зачем тогда о них говорить? Только травить душу.
Поэтому и в истории человечества это число появилось поздно. Торговцы активно использовали счёт, но продавать, например, «ноль овец» не имело смысла. Впрочем, как и отрицательное их количество.
Вышло любопытно: например, древние греки не использовали ноль в принципе, зато уже знали об иррациональных числах, таких как √2. Это было связано с их любовью к геометрии: если у прямоугольного треугольника стороны будут равны 1, длина гипотенузы вычисляется как √2.
Но как же десятеричная система счёта? Ведь даже чтобы записать «10», нам нужен ноль. Но здесь дело только в записи числа: если вы вспомните римские цифры, то поймёте, что десятку можно представить и как Х. Конечно, такая форма была не особенно удобной, но даже вавилоняне, пользовавшиеся позиционной системой счисления (то есть, близкой нашей, а не древнеримской), долго обходились без ноля. Некоторое время его просто не было: числа, скажем, 36 и 306 не различались по написанию и определялись по контексту. Потом его роль стали выполнять два клинышка, вроде вот этих: 3’’6. Но и тогда они самостоятельной роли не играли — не было числа «ноль».
Сложно сказать, когда оно в действительности появилось. При этом есть свидетельства, что в Индии его использовали еще до нашей эры, после чего его переняли арабы, а вот на Западе оно стало входить в практику только в XIII веке усилиями итальянского математика Леонарда Фибоначчи. И то, его любовь к арабскому счислению долго не воспринималась всерьёз.
Чтобы «понять» ноль, нужно немалое интеллектуальное усилие — подобное тому, которое вообще привело к рождению числа как абстракции. Известно, что первые слова, обозначавшие количество, имели конкретное применение — «пять лошадей» и «пять лодок» были для древнего человека разными категориями. Чтобы изобрести ноль, требовалось перейти на новый уровень абстрактного мышления.
Но если мы поверим в ноль, его свойства поразят воображение.
С самыми простыми операциями проблем не возникает: прибавить ноль или вычесть его из числа — число остаётся тем же, умножить на ноль — получится ноль… Всё это укладывается в рамки здравого смысла.
Сложнее становится при возведении в нулевую степень. В школе сообщают, что результатом в каждом случае будет единица. Откуда она взялась?
Тут рассудок уже пасует. Степень — это, как известно, то, сколько раз мы берём число как множитель самого себя.
22 = 2 ∙ 2 = 4
21 = 2
Если степень нулевая, число не является множителем ни разу, но… как из этой пустоты «родилась» единица?
Чаще всего в школе этот вопрос решается догматически: на объяснения не остаётся желания и сил. А ведь именно здесь пролегает одна из границ, за которой простая арифметика, наглядно показываемая на яблоках и прочих исчислимых вещах, становится уже чистой и прекрасной абстракцией.
Вспомним правила обращения с числами, возводимыми в степень, и представим себе следующий пример:
xn/ xn В отношениях с одинаковыми основаниями степеней мы можем делать следующее:
xn/ xn= xn-n = x0 Одновременно с этим мы понимаем, что результат деления любого числа на само себя — это единица. Так вот чудесным образом, благодаря только принятию ноля как числа, мы переходим к новому странному открытию, и математика совершает куда более далёкий прыжок от реальности, чем просто представление «у меня ноль конфет».
Но именно внутренняя логика системы, которая может быть понята умом, но не может быть представлена в вещественном мире — это и есть красота абстракции.
«Деление на ноль как секс — всем можно, а школьникам нет», — шутка может считаться остроумной, но в ней только доля правды. «Деление на ноль» давно стало интернет-мемом, правда, довольно неопределённым. То оно означает аннигиляцию чего бы то ни было (а ведь логичнее было бы умножить на ноль), то вовсе разрушение математических основ мироздания. И второе ближе к истине.
Большинство учёных всё-таки считают эту операцию с нолём невозможной или обладающей неопределённым результатом.

Можете сами провести эксперимент, испытав подручные калькуляторы. Например, телефон на Android у автора материала дал ответ «1 / 0 = ∞», а Windows 10 выдал ошибку: «Деление на ноль невозможно». Большинство других калькуляторов ведёт себя так же. Зато в первом случае можно поменять знак, и мы получим странную картину: «-1 / 0 = -∞».
В чём же дело, и почему даже машины не могут между собой «договориться»?
Чисто арифметически делимость на ноль приводит к рискованным выводам. Смотрите сами:
0 ∙ x = 0 ∙ y, где x и y — два любых произвольных числа. Это лишь известное нам свойство ноля. Но если на него можно делить, то, сократив обе части, мы получим:
х = у Любое число равняется любому числу, что рушит разом сами основы арифметики. Докатились.
Почему же речь иногда заходит о бесконечности? Дело в том, что проблему пытаются решить через деление на бесконечно малую функцию, то есть построение графика функции, где х стремился бы к нулю. Так мы пытаемся найти y = 1 / x, и получается следующее:
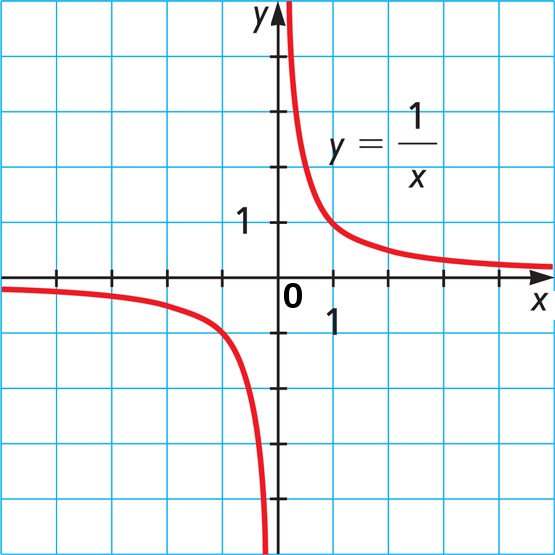
И вот он, наш результат деления на ноль, который уходит в -∞ с одной стороны и +∞ с другой.
Чем же не устраивает этот ответ большинство учёных? Тем, что бесконечность не может быть названа числом: обычные арифметические операции с ней приводят, опять-таки, к парадоксальным выводам.Хоть на ней и построен математический анализ, она является идеей, а не числом.
Можно сказать, что 1 / 0 = ∞ — это просто отговорка, свидетельствующая опять-таки о невозможности операции. Кстати говоря, с делением ноля на ноль наблюдается ещё большее единодушие: тут, если мы соберёмся построить функцию, результаты могут быть практически какими угодно (0, ±1, ±∞…)
В общем, ноль, оставаясь числом, снова подрывает основы математики, если мы нарушаем неприкосновенность его свойств.
Если он так необычен (и не забываем, что он не является ни положительным, ни отрицательным), можно ли говорить о его чётности? Интуитивно мы догадываемся, что он чётный, ведь целые числа сменяют друг друга именно по такому принципу: 2 — чётное, 1 — нечётное, следующим должно быть снова чётное. Но странность ноля настораживает, подсказывает, что и в этом вопросе нужно держать ухо востро.
Парадоксальность как раз в том, что никаких особых свойств у ноля в этом вопросе нет. Он является чётным числом. Какое главное требование он должен пройти в этом случае? Деление на двойку без остатка, и он выдерживает испытание с достоинством:0/2=0. Получается целое число 0, причём сколько бы мы ни продолжали деление, результат будет получаться одинаковым — можно сказать, что он является «наиболее» чётным или «бесконечно» чётным числом.
Если быть более точным, мы должны взять другое определение с обратной операцией. Чётное число может быть представлено в виде 2x, где x — целое число, но и в таком случае всё просто:0 = 2 ∙ 0.
Есть и такое свойство чётных чисел, что при сложении двух из них должно получаться снова чётное, проверим:
0 + 2 = 2; 0 + 4 = 4 и т. д.
При всей необычности ноля даже его удивительное соответствие всем критериям кажется странным, не так ли?
Чтобы узнать больше о ноле как об одном из самых загадочных явлений математики, а также об истории его «открытия», вы можете обратиться к следующим ресурсам:
1. Numberphile. Это популярнейший в среде любителей математики Youtube-канал, у которого уже более чем 1,5 миллиона подписчиков. Есть видео и о ноле в переводе на русский.
2. Книга Чарльза Сейфе «Ноль. Биография опасной идеи». Автор, хоть и не без излишнего сгущения красок, рассказывает об истории ноля как числа и цифры — причем в обширном контексте истории науки, от Архимеда до теории струн. В качестве бонуса вы получите приложения с задачками, где используется ноль. Например, вам предложат доказать, что Уинстон Черчилль был морковкой, и построить машину времени из кротовой дыры.
3. Сборник эссе, в которых фантаст Айзек Азимов рассказывает о том, как человек, переходя от счёта на пальцах ко всё более сложным вычислениям, разработал основные математические операции, а также о том, как числа связаны с нашим восприятием времени и пространства. Природе ноля и его парадоксам посвящена открывающая книгу статья «Nothing Counts».
Также интересно: История чисел: что значили числа в глубокой древности
Числа Фибоначчи
Даже если вам не нравились в школе ни арифметика, ни алгебра, у вас всегда есть возможность ими заинтересоваться. Учить математику с нуля уже не получится — худо-бедно мы начали считать ещё дошколятами. А вот полюбить её с нуля — вполне реальная перспектива.опубликовано
Автор: Кирилл Щедрин
P.S. И помните, всего лишь изменяя свое сознание — мы вместе изменяем мир! ©
Источник: newtonew.com/discussions/zero-in-math
Но любой понимает, что с этим числом не всё в порядке. В детстве, когда мы ещё думали, что арифметика нужна только для счёта, нам объясняли, что ноль — это отсутствие. И это было странно.
Если у меня ноль конфет, считать вообще нечего — зачем тогда о них говорить? Только травить душу.

Поэтому и в истории человечества это число появилось поздно. Торговцы активно использовали счёт, но продавать, например, «ноль овец» не имело смысла. Впрочем, как и отрицательное их количество.
Вышло любопытно: например, древние греки не использовали ноль в принципе, зато уже знали об иррациональных числах, таких как √2. Это было связано с их любовью к геометрии: если у прямоугольного треугольника стороны будут равны 1, длина гипотенузы вычисляется как √2.
Но как же десятеричная система счёта? Ведь даже чтобы записать «10», нам нужен ноль. Но здесь дело только в записи числа: если вы вспомните римские цифры, то поймёте, что десятку можно представить и как Х. Конечно, такая форма была не особенно удобной, но даже вавилоняне, пользовавшиеся позиционной системой счисления (то есть, близкой нашей, а не древнеримской), долго обходились без ноля. Некоторое время его просто не было: числа, скажем, 36 и 306 не различались по написанию и определялись по контексту. Потом его роль стали выполнять два клинышка, вроде вот этих: 3’’6. Но и тогда они самостоятельной роли не играли — не было числа «ноль».
Сложно сказать, когда оно в действительности появилось. При этом есть свидетельства, что в Индии его использовали еще до нашей эры, после чего его переняли арабы, а вот на Западе оно стало входить в практику только в XIII веке усилиями итальянского математика Леонарда Фибоначчи. И то, его любовь к арабскому счислению долго не воспринималась всерьёз.
Чтобы «понять» ноль, нужно немалое интеллектуальное усилие — подобное тому, которое вообще привело к рождению числа как абстракции. Известно, что первые слова, обозначавшие количество, имели конкретное применение — «пять лошадей» и «пять лодок» были для древнего человека разными категориями. Чтобы изобрести ноль, требовалось перейти на новый уровень абстрактного мышления.
Но если мы поверим в ноль, его свойства поразят воображение.
Возвести в нулевую степень
С самыми простыми операциями проблем не возникает: прибавить ноль или вычесть его из числа — число остаётся тем же, умножить на ноль — получится ноль… Всё это укладывается в рамки здравого смысла.
Сложнее становится при возведении в нулевую степень. В школе сообщают, что результатом в каждом случае будет единица. Откуда она взялась?
Тут рассудок уже пасует. Степень — это, как известно, то, сколько раз мы берём число как множитель самого себя.
22 = 2 ∙ 2 = 4
21 = 2
Если степень нулевая, число не является множителем ни разу, но… как из этой пустоты «родилась» единица?
Чаще всего в школе этот вопрос решается догматически: на объяснения не остаётся желания и сил. А ведь именно здесь пролегает одна из границ, за которой простая арифметика, наглядно показываемая на яблоках и прочих исчислимых вещах, становится уже чистой и прекрасной абстракцией.
Вспомним правила обращения с числами, возводимыми в степень, и представим себе следующий пример:
xn/ xn В отношениях с одинаковыми основаниями степеней мы можем делать следующее:
xn/ xn= xn-n = x0 Одновременно с этим мы понимаем, что результат деления любого числа на само себя — это единица. Так вот чудесным образом, благодаря только принятию ноля как числа, мы переходим к новому странному открытию, и математика совершает куда более далёкий прыжок от реальности, чем просто представление «у меня ноль конфет».
Но именно внутренняя логика системы, которая может быть понята умом, но не может быть представлена в вещественном мире — это и есть красота абстракции.
Поделить на ноль
«Деление на ноль как секс — всем можно, а школьникам нет», — шутка может считаться остроумной, но в ней только доля правды. «Деление на ноль» давно стало интернет-мемом, правда, довольно неопределённым. То оно означает аннигиляцию чего бы то ни было (а ведь логичнее было бы умножить на ноль), то вовсе разрушение математических основ мироздания. И второе ближе к истине.
Большинство учёных всё-таки считают эту операцию с нолём невозможной или обладающей неопределённым результатом.

Можете сами провести эксперимент, испытав подручные калькуляторы. Например, телефон на Android у автора материала дал ответ «1 / 0 = ∞», а Windows 10 выдал ошибку: «Деление на ноль невозможно». Большинство других калькуляторов ведёт себя так же. Зато в первом случае можно поменять знак, и мы получим странную картину: «-1 / 0 = -∞».
В чём же дело, и почему даже машины не могут между собой «договориться»?
Чисто арифметически делимость на ноль приводит к рискованным выводам. Смотрите сами:
0 ∙ x = 0 ∙ y, где x и y — два любых произвольных числа. Это лишь известное нам свойство ноля. Но если на него можно делить, то, сократив обе части, мы получим:
х = у Любое число равняется любому числу, что рушит разом сами основы арифметики. Докатились.
Почему же речь иногда заходит о бесконечности? Дело в том, что проблему пытаются решить через деление на бесконечно малую функцию, то есть построение графика функции, где х стремился бы к нулю. Так мы пытаемся найти y = 1 / x, и получается следующее:

И вот он, наш результат деления на ноль, который уходит в -∞ с одной стороны и +∞ с другой.
Чем же не устраивает этот ответ большинство учёных? Тем, что бесконечность не может быть названа числом: обычные арифметические операции с ней приводят, опять-таки, к парадоксальным выводам.Хоть на ней и построен математический анализ, она является идеей, а не числом.
Можно сказать, что 1 / 0 = ∞ — это просто отговорка, свидетельствующая опять-таки о невозможности операции. Кстати говоря, с делением ноля на ноль наблюдается ещё большее единодушие: тут, если мы соберёмся построить функцию, результаты могут быть практически какими угодно (0, ±1, ±∞…)
В общем, ноль, оставаясь числом, снова подрывает основы математики, если мы нарушаем неприкосновенность его свойств.
Ноль — чётное число?
Если он так необычен (и не забываем, что он не является ни положительным, ни отрицательным), можно ли говорить о его чётности? Интуитивно мы догадываемся, что он чётный, ведь целые числа сменяют друг друга именно по такому принципу: 2 — чётное, 1 — нечётное, следующим должно быть снова чётное. Но странность ноля настораживает, подсказывает, что и в этом вопросе нужно держать ухо востро.
Парадоксальность как раз в том, что никаких особых свойств у ноля в этом вопросе нет. Он является чётным числом. Какое главное требование он должен пройти в этом случае? Деление на двойку без остатка, и он выдерживает испытание с достоинством:0/2=0. Получается целое число 0, причём сколько бы мы ни продолжали деление, результат будет получаться одинаковым — можно сказать, что он является «наиболее» чётным или «бесконечно» чётным числом.
Если быть более точным, мы должны взять другое определение с обратной операцией. Чётное число может быть представлено в виде 2x, где x — целое число, но и в таком случае всё просто:0 = 2 ∙ 0.
Есть и такое свойство чётных чисел, что при сложении двух из них должно получаться снова чётное, проверим:
0 + 2 = 2; 0 + 4 = 4 и т. д.
При всей необычности ноля даже его удивительное соответствие всем критериям кажется странным, не так ли?
Что смотреть и читать о ноле?
Чтобы узнать больше о ноле как об одном из самых загадочных явлений математики, а также об истории его «открытия», вы можете обратиться к следующим ресурсам:
1. Numberphile. Это популярнейший в среде любителей математики Youtube-канал, у которого уже более чем 1,5 миллиона подписчиков. Есть видео и о ноле в переводе на русский.
2. Книга Чарльза Сейфе «Ноль. Биография опасной идеи». Автор, хоть и не без излишнего сгущения красок, рассказывает об истории ноля как числа и цифры — причем в обширном контексте истории науки, от Архимеда до теории струн. В качестве бонуса вы получите приложения с задачками, где используется ноль. Например, вам предложат доказать, что Уинстон Черчилль был морковкой, и построить машину времени из кротовой дыры.
3. Сборник эссе, в которых фантаст Айзек Азимов рассказывает о том, как человек, переходя от счёта на пальцах ко всё более сложным вычислениям, разработал основные математические операции, а также о том, как числа связаны с нашим восприятием времени и пространства. Природе ноля и его парадоксам посвящена открывающая книгу статья «Nothing Counts».
Также интересно: История чисел: что значили числа в глубокой древности
Числа Фибоначчи
Даже если вам не нравились в школе ни арифметика, ни алгебра, у вас всегда есть возможность ими заинтересоваться. Учить математику с нуля уже не получится — худо-бедно мы начали считать ещё дошколятами. А вот полюбить её с нуля — вполне реальная перспектива.опубликовано
Автор: Кирилл Щедрин
P.S. И помните, всего лишь изменяя свое сознание — мы вместе изменяем мир! ©
Источник: newtonew.com/discussions/zero-in-math
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.
Профессор Иван Неумывакин: Сода—незаменимый продукт для здоровья
Алис Миллер: Морализаторство только уводит детей с верного пути





































