Las matemáticas de cero: que interesante número 0? Bashny.Net

El cero es, tal vez, el primero en nuestra vida misterioso número. Mucho hemos oído hablar, por ejemplo, acerca de los milagros del número Pi, pero lo poco que tiene con él el asunto en la vida cotidiana. Por no hablar de los números complejos. Pero con el cero en el que nos encontramos en todas partes: incluso en el teclado indica su cifra completa la gama.

Pero cualquiera se da cuenta de que ese número no todo está en orden. En la infancia, cuando todavía pensaba que la aritmética es necesaria solo para la cuenta, nos dijeron que el cero es la ausencia. Y esto era extraño.

Si tengo cero dulces, contar en absoluto nada — ¿por qué entonces hablar de ellos? Sólo envenenar el alma.

Por lo tanto, y en la historia de la humanidad es el número apareció tarde. Los comerciantes han utilizado la cuenta, pero vender, por ejemplo, "cero ovejas", no tenía sentido. Sin embargo, como el negativo de su número.

Salió curioso: por ejemplo, los antiguos griegos no usaban el cero en principio, pero ya lo sabía de números irracionales, tales como √2. Esto tenía que ver con su amor a la geometría: si la hipotenusa de un triángulo partes son iguales a 1, la longitud de la гипотенузы se calcula como √2.

Pero, ¿cómo decimal información del sistema de cuentas? Después de todo, incluso para grabar el "10" necesitamos un cero. Pero aquí el asunto sólo en la escritura de números: si usted recuerda los números romanos, se dará cuenta de que la decena se pueden presentar y como C. por Supuesto, esta forma no era especialmente cómodo, pero incluso los babilonios, utilizando un sistema de colocación numérico (es decir, cercana a la nuestra, y no romana), el tiempo que pasaban sin cero. De un tiempo simplemente no lo es: el número de, digamos, 36 y 306 no se diferenciaban en la redacción y estaban determinados por el contexto. Luego de su papel a cumplir dos клинышка, como estos: 3"6. Pero y entonces independiente de la función de no jugar — no es el número "cero".

Es difícil de decir, cuando es en realidad apareció. Hay evidencias de que en la india, utilizado antes de nuestra era, después de que la adoptaron los árabes, y aquí en Occidente se ha convertido en entrar en la práctica sólo en el siglo XIII los esfuerzos italiano matemático leonardo fibonacci. Y entonces, su amor a la árabe счислению mucho tiempo no ha sido considerada en serio.

Para "comprender" el cero, se necesita bastante inteligente de la fuerza similar a la que en general ha llevado al nacimiento de los números como de la abstracción. Se sabe que las primeras palabras, обозначавшие número, tuvieron la aplicación concreta de cinco de los caballos" y "cinco barcos fueron para el hombre primitivo diferentes categorías. Para inventar de cero, era necesario pasar a un nuevo nivel de pensamiento abstracto.

Pero si creemos en cero, sus propiedades llegará a la imaginación.

  Construir en el grado cero de la

Con el más simple de las operaciones no es un problema: añadir cero o restar de un número — el número sigue siendo el mismo, multiplicar por cero — tendrá cero... Todo esto dentro de un marco de sentido común.

Es más difícil cuando la edificación en cero grado. En la escuela informan de que el resultado en cada caso será una unidad. De dónde viene?

Aquí la razón ya se ha retirado. El grado es, como se sabe, el número de veces que tomamos el número como el multiplicador de sí mismo.

22 = 2 ∙ 2 = 4

21 = 2

Si el grado cero, el número no se multiplica ninguna vez, pero... ¿cómo de ese vacío "nació" la unidad?

Más a menudo en la escuela a este tema se dogmáticamente: en la explicación, no se queda el deseo y la fuerza. Y es precisamente aquí va uno de los límites, por el cual la simple aritmética, de un modo evidente que en manzanas y otros исчислимых cosas, se convierte en pura y hermosa abstracción.

Recordemos la regla de trato con los números, возводимыми en el grado, y supongamos el siguiente ejemplo:

xn/ xn En relación con los mismos motivos de los grados podemos hacer lo siguiente:

xn/ xn= xn-n = x0 al mismo tiempo somos conscientes de que el resultado de dividir cualquier número por sí mismo es una unidad. Así milagrosamente, gracias sólo a la adopción de cero como número, pasamos a una nueva extraño descubrimiento y matemáticas hace mucho más lejano que el salto de la realidad, que es sólo la presentación de "tengo cero dulces".

Pero ésa es la lógica interna del sistema, que puede ser comprendido por la mente, pero no puede ser representada en el mundo real, es la belleza de la abstracción.

 Dividir por cero

"División por cero como el sexo todo se puede, y los alumnos no", la broma puede considerarse ingeniosa, pero en ella sólo parte de la verdad. "División por cero" ha sido durante mucho tiempo el internet de la pica, la verdad, es bastante incierto. Lo que significa - lo que sea (y de hecho lógico sería multiplicar por cero), lo absoluto la destrucción de los fundamentos matemáticos del universo. Y la segunda, más cerca de la verdad.

La mayoría de los científicos todavía consideran que esta operación con нолем imposible o con resultados inciertos.





Puede realizar el experimento, después de haber experimentado compañeros de calculadoras. Por ejemplo, un teléfono Android de el autor de la presentación dio la respuesta "1 / 0 = ∞", y Windows 10 ha emitido un error: "error de División por cero no se puede". La mayoría de los otros calculadores se comporta de la misma. Pero en el primer caso, puede cambiar el signo, y obtenemos la extraña visión: "-1 / 0 = -∞".

¿Qué pasa, y por qué incluso las máquinas no pueden entre sí "ponerse de acuerdo"?

Puramente por la via del cálculo mostrado en cero conduce a la arriesgado conclusiones. Véase a sí mismo:

0 ∙ x = 0 ∙ y, donde x e y son dos arbitrarias de un número. Esto es sólo conocido a la propiedad de cero. Pero si en él se puede dividir, reduciendo ambas partes, obtenemos:

x = Cualquier número es igual a cualquier número, que destruye la vez los fundamentos de la aritmética. Alcanzaron.

¿Por qué a veces se trata de infinito? El caso es que el problema que tratan de resolver a través de la división en infinitamente pequeña de la función, es decir, la construcción de la gráfica de la función, donde x aspiraba a cero. Así tratamos de encontrar y = 1 / x, y se obtiene lo siguiente:





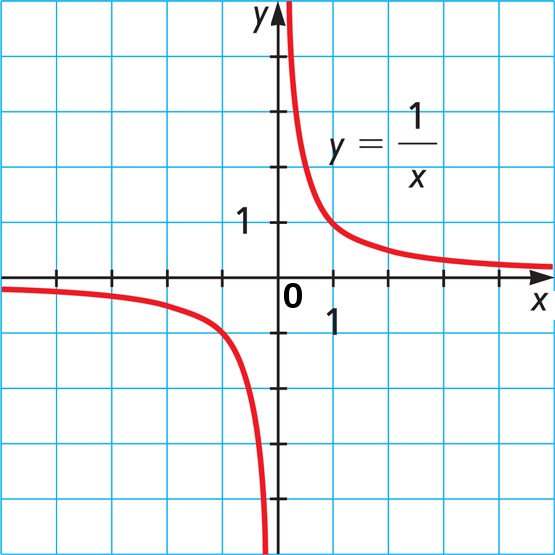
Y aquí está, nuestro resultado de la división por cero, que se va de -∞ a un lado, y +∞ por otro.

El que no está satisfecho con la respuesta de la mayoría de los científicos? El hecho de que el infinito no puede ser nombrado el número de: las operaciones aritméticas con ella llevan, de nuevo, a rus.Aunque en ella y construido análisis matemático, ella es a la idea, y no un número.

Se puede decir que 1 / 0 = ∞ es simplemente la excusa que demuestre que, de nuevo, sobre la imposibilidad de la operación. Por cierto, con la división cero a cero se observa una mayor unanimidad: aquí, si tenemos intención de construir una función, los resultados pueden ser casi cualquier cosa (0, ±1, ±∞...)

En general, cero, manteniéndose el número, de nuevo, socava los fundamentos de las matemáticas, si se nos rompe la integridad de sus propiedades.

 

El cero es un número par?

Si es tan poco común (y no olvidamos, que no es ni positivo, ni negativo), ¿se puede hablar de su paridad? Intuitivamente nos damos cuenta de que él incluso, ya que los números enteros sucesión precisamente en este principio: 2 — par, 1 — impar, el siguiente debe ser nuevo par. Pero la singularidad de cero alarmante, se sugiere que en ese sentido es necesario mantener el oído los ojos bien abiertos.

Paradoja que justamente en el hecho de que no hay propiedades especiales de el cero en este tema, no. Es un número par. ¿Cuál es el principal requisito que debe tomar en este caso? La división en un f sin que el resto, y puede soportar la prueba con dignidad:0/2=0. Se obtiene un número entero de 0, y aunque hemos siguieron la división, el resultado será obtenida de la misma — se puede decir que él es "más" par o "infinito" de un número par.

Para ser más precisos, debemos tomar otra definición con la operación inversa. Un número par puede ser representado como el 2x, donde x es un número entero, pero en este caso es muy sencillo:0 = 2 ∙ 0.

Hay una propiedad de los números pares, que la suma de dos de ellos debe resultar de nuevo par, veamos:

0 + 2 = 2; 0 + 4 = 4 etc.

Cuando toda la singularidad de cero, incluso su maravilloso el cumplimiento de todos los criterios parece extraño, ¿no?

 Que ver y leer acerca de nole?

Para saber más sobre el cero como uno de los fenómenos más misteriosos de las matemáticas, así como sobre la historia de su "descubrimiento", se puede acceder a los siguientes recursos:

 

1. Numberphile. Es ms popular en el entorno de los amantes de las matemáticas Youtube-canal, que tiene ya más de 1,5 millones de suscriptores. Hay videos y sobre el cero en la traducción al ruso.

 

2. El Libro De Charles De La Caja Fuerte De Cero. Biografía de una idea peligrosa". El autor, aunque no sin excesiva concentración de pinturas, habla sobre la historia de cero de números y de figuras y en el amplio contexto de la historia de la ciencia, de arquímedes a la teoría de las cuerdas. Como bonificación que se obtiene de la aplicación con задачками, donde se utiliza el cero. Por ejemplo, sirve para demostrar que winston churchill fue por la zanahoria, y construir una máquina del tiempo de кротовой agujeros.

 

3. Libro de ensayos, en los que la novela de ficción isaac asimov habla de cómo el hombre, pasando de la cuenta en los dedos a la vez más compleja a la computación, en la que desarrolló las principales operaciones matemáticas, así como el número de asociados con nuestra percepción del tiempo y del espacio. La naturaleza de cero y su парадоксам dedicado a la apertura de un libro de un artículo de "Nothing Counts".

 

También es interesante: la Historia de los números: que significaban los números en la antigüedad

Los Números De Fibonacci

 

Incluso si no te gustaban en la escuela ni aritmética ni álgebra, siempre tienes la posibilidad de interesarse por ellos. Aprender matemáticas desde cero ya no funciona — mal-mal hemos empezado a considerar aún дошколятами. Y aquí es amar desde cero es un verdadero punto de vista.publicado

Autor: Cirilo Щедрин

 

P. S. Y recuerde, sólo cambiando su conciencia — estamos juntos cambiando el mundo! ©

Fuente: newtonew.com/discussions/zero-in-math