1009
Математика з нуля: що цікаве число 0?
Зеро, мабуть, перший таємничий номер у нашому житті. Ми чули багато про чудеса пі, наприклад, але мало людей, які займаються ним в повсякденному житті. Не кажучи вже про складні номери. Але з нульовим, ми поїдемо по всьому світу: навіть на клавіатурі, кількість, яка позначається її завершує серію.
Але всі розуміють, що це число не все правильно. Коли ми були діти, коли ми думали, що арифметичне було просто для підрахунку, ми сказали, що нульовий був відсутнім. І був дивний.
Якщо у мене є нульова цукерка, нічого не зарахувати - то чому говорити про них? Просто отруюйте душу.
Тому в історії людства цей номер з'явився пізно. У зв’язку з тим, що «з нуля» не було сенсу. Однак, а також їх негативний номер.
Він був пишним. Наприклад, давні греки не використовували нуль за принципом, але вони вже знали про ірраціональні числа, такі як √2. Це було пов'язано з їх любов'ю геометрії: якщо правий трикутник має сторони, рівні до 1, довжина гіпотенусу розраховується як √2.
Але що про десяткову систему? Навіть писати 10, потрібно нуль. Але ось це просто справа запису номеру: якщо ви пам'ятаєте римські цифри, ви дізнаєтеся, що десять може бути представлений як X. Звісно, ця форма не була особливо зручною, але навіть вавилоняни, які використовували вегетативну систему цифр (тобто близько до нас, не давнього Риму), тривалий час зуміли без нуля. В той час, як це просто не було: цифри, скажуть 36 і 306, не відрізнялися від написання і були визначені контекстом. Тоді він був відтворений двома клятами, такими як: 3'6. Але навіть тоді вони не відіграли незалежну роль - не було число «зеро».
Важко сказати, що він насправді прийшов в істоту. У той же час, є докази, що в Індії він був використаний до нашої ери, після чого він був прийнятий арабами, але на Заході він почав вступати в практику тільки в XIII столітті за зусиллями італійського математика Леонард Фібоначчі. Його любов арабської не забрав серйозно протягом тривалого часу.
Для «підтримки» нуль вимагає значних інтелектуальних зусиль, схожих на те, що призвело до народження числа як абстракції. Відомий, що перші слова, денотували кількість, мали специфічне застосування - "п'ять коней" і "п'ять катерів" були різні категорії для давньої людини. Для того, щоб винахідити нуль, нам довелося переходити на новий рівень абстрактного мислення.
Але якщо ми віримо в нуль, її властивості здивує уяву.
Зеро-дегре.
З найпростішими операціями немає проблем: додати нульовий або відхилити його з числа - номер залишається таким же, розмножуватися нуль - ви отримуєте нуль. Все це в рамках спільного почуття.
При створенні нульового ступеня стає складніше. Школа говорить результат буде одним у кожному випадку. Де це сталося?
Немає причин. Ступінь, скільки разів ми беремо на себе номер, як мультиплікатор.
22 = 2∙ 2 = 4
21 = 2
Якщо потужність є нульовим, число ніколи не є багатоплічником, але ... як було з цього недійсним?
Дуже часто в школі, це питання вирішується собачаматично: не існує бажання і сила пояснювати. Але тут лежить одна з меж, які просте арифметичне, чітко показано на яблуні та інших занурюваних речей, стає чистою і красивою абстракцією.
Звертаємо Вашу увагу на те, що ми працюємо з числами, які піднялися до влади, і уявімо наступний приклад:
ксн/ксн Що стосується однакових ступенів, ми можемо зробити наступне:
xn / xn = xn = x0 У той же час ми розуміємо, що результат поділу будь-якого числа сама собою є блоком. Тепер, дивно, просто, приймаючи нуль як номер, ми переїжджаємо на дивне нове відкриття, і математика займає набагато далі стрибка від реальності, ніж просто поняття «Я отримав нуклейки».
Але це внутрішня логіка системи, яка може бути зрозуміла розумом, але не може бути представлена в матеріальному світі, що є красою абстракції.
Дивид нульовим
«Дівід нулю подобається секс – кожен може, але не школярі» – жарт можна вважати життєздатним, але це тільки дроб істини. «Дівід нулю» вже давно став інтернет-мемою, але досить ваговим. Це означає, що анігілація будь-якого (і це буде більш логічно розмножуватися нуль), або руйнування математичних основ Всесвіту. І другий ближче до правди.
Більшість вчених вважають, що це нульова операція неможливе або з невизначеним результатом.

Ви можете самі експериментувати за допомогою тестування калькуляторів. Наприклад, автор телефону Android дав відповідь.1/0 = ∞Windows 10 дав помилку: «Дівід нульовим неможливим». Більшість інших калькуляторів, які полягають таким же чином. Але в першому випадку можна змінити знак, і ми отримуємо дивну картину:-1/0 = -З?
Що таке справа, і чому не можна навіть машин «необхідно» один з одним?
Чистий арифметично, дивізимність нульовим призводить до ризикованих висновків. Побачити себе:
0 ∙ x = 0 ∙ y, де x і y є будь-якими двома довільними числами. Це просто властивість нулю ми знаємо. Але якщо його можна розділити на дві частини, ми отримуємо:
x = y Будь-який номер дорівнює будь-якій кількості, яка знищує дуже фундаменти арифметизму одночасно. Це над.
Чому ми іноді говоримо про нескінченність? Справа в тому, що вони намагаються вирішити проблему, поділившись на нескінченну функцію, тобто побудови графіка функції, де до Я знаходжу до нуля. Ось як ми намагаємося знайти Р = 1/ксІ ви отримаєте це:
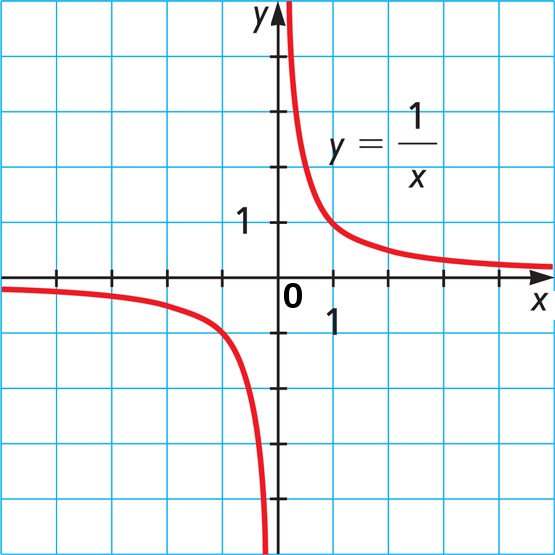
І ось, наш результат ділиться нульом, що йде в - ∞ з одного боку до + Інше
Яка відповідь від більшості вчених? Справа в тому, що нескінченність не може називатися числом: звичайні арифметичні операції з ним ведуть, знову, до парадоксичних висновків.Хоча математичний аналіз побудований на ньому, це ідея, не число.
Це можна сказати, що 1/0 = ∞ Це просто виправдання, що вказується знову, що операція неможлива. До речі, є ще більша нерівність щодо поділу нуль на нульовий: тут, якщо ми збираємося будувати функцію, результати можуть бути досить багато чого. 0 товар(ов) - 0.00 €
В цілому, нуль, що залишився ряд, знову підмінює основи математики, якщо порушується цілісність її властивостей.
Зеро - це навіть число?
Якщо це так незвично (і ми не забуваємо, що це не позитивне, ні негативно), ми можемо говорити про його парність? Імовірно, ми вгадаємо, що це навіть, оскільки цілі замінюють один одного за цим принципом: 2 парі, 1 непарний, наступний повинен бути ще раз. Але дивність нулю є тривожним, говорить про те, що в цьому питанні потрібно тримати вуха відкритим.
Парадокс є те, що не існує спеціальних властивостей нулю в цьому питанні. Це парний номер. Що таке головна вимога, яку він повинен пройти в цьому випадку? Дайд в два без решти, і він проходить тест з гідністю:0/2=0й Результатом є ціле 0, і неважливо, скільки ми продовжуємо ділимося, результат буде таким же – ми можемо сказати, що це «найбільший» навіть або «інфінітивно» навіть число.
Щоб бути більш точним, ми повинні прийняти різне визначення з зворотною хірургією. Навіть номер може бути представлений як 2ксде x є цілим, але в цьому випадку це просто:0 = 2 ∙ 0й
Також є така властивість парних чисел, які при додаванні двох з них, необхідно знову отримати, перевірити:
0 + 2 = 2; 0 + 4 = 4;
Для всіх незвичайностей нуль, навіть його дивовижна комплаєнс всіх критеріїв здається дивним, правим?
Що дивитися і читати про нуль?
Щоб дізнатися більше про нулю, як одне з найбільш загадкових явищ математики, а також історії його «відкритого», можна звернутися до наступних ресурсів:
1,1 км Кількістьфілів.Найпопулярніші серед анімаційних каналів YouTube, які вже налічує понад 1,5 млн абонентів. Відео про нульову мову російською мовою.
2. Карл Сеіф книги Зеро. Біографія небезпечної ідеї.Автор, хоча не без надмірного загущення кольорів, розповідає про історію нулю як номер і число - і в переважному контексті історії науки, з архімдів до теорії струн. Як бонус, ви отримаєте додатки з завданнями, де використовується нульовий. Наприклад, ви попросите довести, що Winston Churchill був морквою і збудувати час машини з гельмінта.
3. У Збір есе, в якому наукова фантастика Ісаак Асимов Про те, як люди, так як вони переходять від підрахунку на своїх пальцях до більш складних обчислень, розвивалися основні математичні операції, і як цифри відносяться до нашого сприйняття часу і простору. Природа нулю та її парадоксів присвячена отворній статті «Нові графи».
Цікаво: Історія номерів: які номери означали в давнину
Фібоначчі числа
Навіть якщо ви не любите арифметичне або алгебра в школі, ви завжди маєте можливість зацікавити їх. Не можна вчити математику з нуля - ми почали розглянути дошкільки в будь-який час. Але, щоб любити її від нуля, є дуже реальним перспективою. Видання
Кредит: Кирило Щедрін
П.С. І пам'ятайте, що лише змінивши вашу свідомість – разом ми змінюємо світ!
Джерело: newtonew.com/discussions/zero-in-mat
Але всі розуміють, що це число не все правильно. Коли ми були діти, коли ми думали, що арифметичне було просто для підрахунку, ми сказали, що нульовий був відсутнім. І був дивний.
Якщо у мене є нульова цукерка, нічого не зарахувати - то чому говорити про них? Просто отруюйте душу.

Тому в історії людства цей номер з'явився пізно. У зв’язку з тим, що «з нуля» не було сенсу. Однак, а також їх негативний номер.
Він був пишним. Наприклад, давні греки не використовували нуль за принципом, але вони вже знали про ірраціональні числа, такі як √2. Це було пов'язано з їх любов'ю геометрії: якщо правий трикутник має сторони, рівні до 1, довжина гіпотенусу розраховується як √2.
Але що про десяткову систему? Навіть писати 10, потрібно нуль. Але ось це просто справа запису номеру: якщо ви пам'ятаєте римські цифри, ви дізнаєтеся, що десять може бути представлений як X. Звісно, ця форма не була особливо зручною, але навіть вавилоняни, які використовували вегетативну систему цифр (тобто близько до нас, не давнього Риму), тривалий час зуміли без нуля. В той час, як це просто не було: цифри, скажуть 36 і 306, не відрізнялися від написання і були визначені контекстом. Тоді він був відтворений двома клятами, такими як: 3'6. Але навіть тоді вони не відіграли незалежну роль - не було число «зеро».
Важко сказати, що він насправді прийшов в істоту. У той же час, є докази, що в Індії він був використаний до нашої ери, після чого він був прийнятий арабами, але на Заході він почав вступати в практику тільки в XIII столітті за зусиллями італійського математика Леонард Фібоначчі. Його любов арабської не забрав серйозно протягом тривалого часу.
Для «підтримки» нуль вимагає значних інтелектуальних зусиль, схожих на те, що призвело до народження числа як абстракції. Відомий, що перші слова, денотували кількість, мали специфічне застосування - "п'ять коней" і "п'ять катерів" були різні категорії для давньої людини. Для того, щоб винахідити нуль, нам довелося переходити на новий рівень абстрактного мислення.
Але якщо ми віримо в нуль, її властивості здивує уяву.
Зеро-дегре.
З найпростішими операціями немає проблем: додати нульовий або відхилити його з числа - номер залишається таким же, розмножуватися нуль - ви отримуєте нуль. Все це в рамках спільного почуття.
При створенні нульового ступеня стає складніше. Школа говорить результат буде одним у кожному випадку. Де це сталося?
Немає причин. Ступінь, скільки разів ми беремо на себе номер, як мультиплікатор.
22 = 2∙ 2 = 4
21 = 2
Якщо потужність є нульовим, число ніколи не є багатоплічником, але ... як було з цього недійсним?
Дуже часто в школі, це питання вирішується собачаматично: не існує бажання і сила пояснювати. Але тут лежить одна з меж, які просте арифметичне, чітко показано на яблуні та інших занурюваних речей, стає чистою і красивою абстракцією.
Звертаємо Вашу увагу на те, що ми працюємо з числами, які піднялися до влади, і уявімо наступний приклад:
ксн/ксн Що стосується однакових ступенів, ми можемо зробити наступне:
xn / xn = xn = x0 У той же час ми розуміємо, що результат поділу будь-якого числа сама собою є блоком. Тепер, дивно, просто, приймаючи нуль як номер, ми переїжджаємо на дивне нове відкриття, і математика займає набагато далі стрибка від реальності, ніж просто поняття «Я отримав нуклейки».
Але це внутрішня логіка системи, яка може бути зрозуміла розумом, але не може бути представлена в матеріальному світі, що є красою абстракції.
Дивид нульовим
«Дівід нулю подобається секс – кожен може, але не школярі» – жарт можна вважати життєздатним, але це тільки дроб істини. «Дівід нулю» вже давно став інтернет-мемою, але досить ваговим. Це означає, що анігілація будь-якого (і це буде більш логічно розмножуватися нуль), або руйнування математичних основ Всесвіту. І другий ближче до правди.
Більшість вчених вважають, що це нульова операція неможливе або з невизначеним результатом.

Ви можете самі експериментувати за допомогою тестування калькуляторів. Наприклад, автор телефону Android дав відповідь.1/0 = ∞Windows 10 дав помилку: «Дівід нульовим неможливим». Більшість інших калькуляторів, які полягають таким же чином. Але в першому випадку можна змінити знак, і ми отримуємо дивну картину:-1/0 = -З?
Що таке справа, і чому не можна навіть машин «необхідно» один з одним?
Чистий арифметично, дивізимність нульовим призводить до ризикованих висновків. Побачити себе:
0 ∙ x = 0 ∙ y, де x і y є будь-якими двома довільними числами. Це просто властивість нулю ми знаємо. Але якщо його можна розділити на дві частини, ми отримуємо:
x = y Будь-який номер дорівнює будь-якій кількості, яка знищує дуже фундаменти арифметизму одночасно. Це над.
Чому ми іноді говоримо про нескінченність? Справа в тому, що вони намагаються вирішити проблему, поділившись на нескінченну функцію, тобто побудови графіка функції, де до Я знаходжу до нуля. Ось як ми намагаємося знайти Р = 1/ксІ ви отримаєте це:

І ось, наш результат ділиться нульом, що йде в - ∞ з одного боку до + Інше
Яка відповідь від більшості вчених? Справа в тому, що нескінченність не може називатися числом: звичайні арифметичні операції з ним ведуть, знову, до парадоксичних висновків.Хоча математичний аналіз побудований на ньому, це ідея, не число.
Це можна сказати, що 1/0 = ∞ Це просто виправдання, що вказується знову, що операція неможлива. До речі, є ще більша нерівність щодо поділу нуль на нульовий: тут, якщо ми збираємося будувати функцію, результати можуть бути досить багато чого. 0 товар(ов) - 0.00 €
В цілому, нуль, що залишився ряд, знову підмінює основи математики, якщо порушується цілісність її властивостей.
Зеро - це навіть число?
Якщо це так незвично (і ми не забуваємо, що це не позитивне, ні негативно), ми можемо говорити про його парність? Імовірно, ми вгадаємо, що це навіть, оскільки цілі замінюють один одного за цим принципом: 2 парі, 1 непарний, наступний повинен бути ще раз. Але дивність нулю є тривожним, говорить про те, що в цьому питанні потрібно тримати вуха відкритим.
Парадокс є те, що не існує спеціальних властивостей нулю в цьому питанні. Це парний номер. Що таке головна вимога, яку він повинен пройти в цьому випадку? Дайд в два без решти, і він проходить тест з гідністю:0/2=0й Результатом є ціле 0, і неважливо, скільки ми продовжуємо ділимося, результат буде таким же – ми можемо сказати, що це «найбільший» навіть або «інфінітивно» навіть число.
Щоб бути більш точним, ми повинні прийняти різне визначення з зворотною хірургією. Навіть номер може бути представлений як 2ксде x є цілим, але в цьому випадку це просто:0 = 2 ∙ 0й
Також є така властивість парних чисел, які при додаванні двох з них, необхідно знову отримати, перевірити:
0 + 2 = 2; 0 + 4 = 4;
Для всіх незвичайностей нуль, навіть його дивовижна комплаєнс всіх критеріїв здається дивним, правим?
Що дивитися і читати про нуль?
Щоб дізнатися більше про нулю, як одне з найбільш загадкових явищ математики, а також історії його «відкритого», можна звернутися до наступних ресурсів:
1,1 км Кількістьфілів.Найпопулярніші серед анімаційних каналів YouTube, які вже налічує понад 1,5 млн абонентів. Відео про нульову мову російською мовою.
2. Карл Сеіф книги Зеро. Біографія небезпечної ідеї.Автор, хоча не без надмірного загущення кольорів, розповідає про історію нулю як номер і число - і в переважному контексті історії науки, з архімдів до теорії струн. Як бонус, ви отримаєте додатки з завданнями, де використовується нульовий. Наприклад, ви попросите довести, що Winston Churchill був морквою і збудувати час машини з гельмінта.
3. У Збір есе, в якому наукова фантастика Ісаак Асимов Про те, як люди, так як вони переходять від підрахунку на своїх пальцях до більш складних обчислень, розвивалися основні математичні операції, і як цифри відносяться до нашого сприйняття часу і простору. Природа нулю та її парадоксів присвячена отворній статті «Нові графи».
Цікаво: Історія номерів: які номери означали в давнину
Фібоначчі числа
Навіть якщо ви не любите арифметичне або алгебра в школі, ви завжди маєте можливість зацікавити їх. Не можна вчити математику з нуля - ми почали розглянути дошкільки в будь-який час. Але, щоб любити її від нуля, є дуже реальним перспективою. Видання
Кредит: Кирило Щедрін
П.С. І пам'ятайте, що лише змінивши вашу свідомість – разом ми змінюємо світ!
Джерело: newtonew.com/discussions/zero-in-mat
Професор Іван Неймивакін: Сода - незамінний продукт для здоров'я
Аліса Міллер: Moralization приймає дітей з правої доріжки























