714
Забудьте калькулятор! Ці 10 математики не навчать вас в школі.
Математика не як складна наука, як вона може здатися на перший погляд. У вас є багато секретів, які дозволяють зробити дуже складні розрахунки. Якщо у вас є багато порад, щоб залишити в офіціантці, або якщо у вас є жорсткий час, віддаючи ресторанний рахунок, ці 10 хитрощів просто для вас. А до речі, це чудовий теплий макіяж для вашого мозку!
Як отримати 15% будь-якого числа
Вам необхідно спочатку відрахувати 10% від неї, а потім розділити отриманий номер на 2 і додати ці цифри.
Приклад: 15% від 358
1,1 км Знайти 10% - 35.8.
2,2 км Знайдіть половину 35.8 - 17.9.
3. У Додайте 17.9 до 35.8 і ви отримаєте 53.7.
Множення "3 по 1" в свідомості
Ви не знаєте, як це просто. Ви просто повинні розділити велике завдання на кілька маленьких.
Приклад: 450 х 6
1,1 км Дивід 450 в два прості номери: 400 і 50.
2. Мульті 400 по 6 і 50 по 6 окремо (2,400 і 300).
3. У Додайте отримані числа (2,700).
Кількість двох чисел
З цим трюком ви збираєтеся на квадратні дві цифри дуже швидко. Все, що потрібно зробити, ділити номер двома і отримати приблизну відповідь.
Приклад: 53кс2
1,1 км Відстежуйте 3 з 53, щоб отримати 50, і додайте 3 до 53, щоб отримати 56.
2,2 км Багатомовно два числа, використовуючи попередні поради (50 х 56 = 2800).
3. У Додайте квадрат номеру, на який ви знизили і збільшили 53 (2800 + 3^2 = 2809).
Секрет є те, що коли ви квадратні дві цифри, вам потрібно перетворювати їх в цифри, які набагато простіше розмножуватися, так як ми зробили з 53.
Передача номеру в 5
З цією математичною роботою все ще простіше. Прийміть перший номер квадрата. Багатомовно це однаковим числом плюс 1,1 км Потім додайте число 25 в кінці.
Приклад: 85^2 Р
1,1 км 8 по 9 і ви отримаєте 72.
2,2 км До 25 і ви отримаєте 7225.
Відділ по одному номеру
Вибачте свою думку, вам потрібно майже щодня.
Приклад: 589: 7
1,1 км Необхідно знайти приблизні відповіді, помножуючи 8 за номерами, які дають екстремальні результати (7 × 80 = 560, 7 × 90 = 630). Відповідь 80-plus.
2. Відправлення 560 від 589. Якщо ви отримуєте номер 29, розділіть його на 7 і ви отримаєте 4 з рештою 1.
3. Відповідь - 84.1
Відповідь, звичайно, не найточніше, але навіть ця відповідь буде достатньо для вас, наприклад, оплати в ресторані.
Як швидко знайти кубічні корені чисел
Щоб легко знайти корінь куба з будь-якого числа, потрібно вивчити кубики чисел від 1 до 10:
1 - 1
2 - 8
3 - 27
4 - 64
5 - 125
6 - 216
7 - 343
8 - 512
9 - 729
до 1000
Знаючи їх серцем, можна легко знайти кубічний корінь будь-якого числа.
Приклад: кубічний корінь 39,304
1,1 км Візьміть величину тисяч (39) і знайдіть між ними числа (27 і 64). Це означає, що перша цифра в відповідь 3, і відповідь в діапазоні 30.
2,2 км Кожна цифра від 0 до 9 з'являється в кубічних коренях чисел від 1 до 10 тільки один раз.
3. У З останньої цифри в нашому випадку 4, що означає, що остання цифра відповіді буде 4, так як в її кубічному корені остання цифра 4.
4. У Відповідь 34.
Русь 70
Щоб дізнатися, скільки років ви можете подвоювати гроші, розділіть номер 70 за річним процентним ставком.
Приклад:Скільки коштує подвійні гроші з річним процентним ставком на 17%?
70:17 = 4.1 років
Рулі 110
Щоб дізнатися, скільки років ви можете потроїти гроші, потрібно розділити число 110 на річний процентний ставок.
Приклад:Скільки років займає потрійні гроші на щорічній процентній ставці 20%?
110: 20 = 5.5 років
Магія No1089
І цей трюк здивує всіх! Подумайте про будь-який трицифровий номер, цифри якого в порядку зменшення, наприклад 642 або 864. Далі напишіть його в зворотному порядку і відніміть його з початкового числа. До отриманого числа додають той же номер, тільки письмовий в зворотному порядку. Що робити? 1089?
простий трюк.
Ви, ймовірно, бачили цей трюк багато: Подумайте про будь-який номер. Навколо його на 2. Додати 12. Розділіть його на 2. Відстежуйте оригінальний номер з нього.
Ви отримали 6, ви не отримали? Що б ви хочете, ви все ще отримаєте 6. І ось чому:
1,1 км 2,2 км
2. 2 + 12
3. (2 + 12): 2 = + 6
4. + 6 -
Це основні правила алгебри, і зараз ці хитрощі не здивують вас.
Не дивно, чому ми не навчаємо цього в школі. Виявляється, що багатозастосування стовпців застаріла, і ці секрети набагато корисніше, ніж більшість з яких ми навчалися в класах математики.
Покажіть ваші друзі, як зробити складні математичні розрахунки у вашому розумі!
через takprosto cc
Як отримати 15% будь-якого числа
Вам необхідно спочатку відрахувати 10% від неї, а потім розділити отриманий номер на 2 і додати ці цифри.
Приклад: 15% від 358
1,1 км Знайти 10% - 35.8.
2,2 км Знайдіть половину 35.8 - 17.9.
3. У Додайте 17.9 до 35.8 і ви отримаєте 53.7.
Множення "3 по 1" в свідомості
Ви не знаєте, як це просто. Ви просто повинні розділити велике завдання на кілька маленьких.
Приклад: 450 х 6
1,1 км Дивід 450 в два прості номери: 400 і 50.
2. Мульті 400 по 6 і 50 по 6 окремо (2,400 і 300).
3. У Додайте отримані числа (2,700).
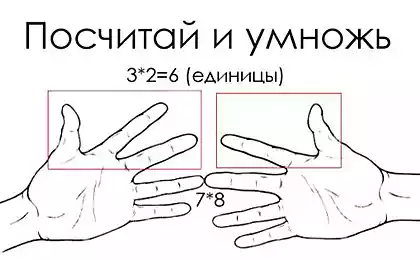
Кількість двох чисел
З цим трюком ви збираєтеся на квадратні дві цифри дуже швидко. Все, що потрібно зробити, ділити номер двома і отримати приблизну відповідь.
Приклад: 53кс2
1,1 км Відстежуйте 3 з 53, щоб отримати 50, і додайте 3 до 53, щоб отримати 56.
2,2 км Багатомовно два числа, використовуючи попередні поради (50 х 56 = 2800).
3. У Додайте квадрат номеру, на який ви знизили і збільшили 53 (2800 + 3^2 = 2809).
Секрет є те, що коли ви квадратні дві цифри, вам потрібно перетворювати їх в цифри, які набагато простіше розмножуватися, так як ми зробили з 53.
Передача номеру в 5
З цією математичною роботою все ще простіше. Прийміть перший номер квадрата. Багатомовно це однаковим числом плюс 1,1 км Потім додайте число 25 в кінці.
Приклад: 85^2 Р
1,1 км 8 по 9 і ви отримаєте 72.
2,2 км До 25 і ви отримаєте 7225.
Відділ по одному номеру
Вибачте свою думку, вам потрібно майже щодня.
Приклад: 589: 7
1,1 км Необхідно знайти приблизні відповіді, помножуючи 8 за номерами, які дають екстремальні результати (7 × 80 = 560, 7 × 90 = 630). Відповідь 80-plus.
2. Відправлення 560 від 589. Якщо ви отримуєте номер 29, розділіть його на 7 і ви отримаєте 4 з рештою 1.
3. Відповідь - 84.1
Відповідь, звичайно, не найточніше, але навіть ця відповідь буде достатньо для вас, наприклад, оплати в ресторані.
Як швидко знайти кубічні корені чисел
Щоб легко знайти корінь куба з будь-якого числа, потрібно вивчити кубики чисел від 1 до 10:
1 - 1
2 - 8
3 - 27
4 - 64
5 - 125
6 - 216
7 - 343
8 - 512
9 - 729
до 1000
Знаючи їх серцем, можна легко знайти кубічний корінь будь-якого числа.
Приклад: кубічний корінь 39,304
1,1 км Візьміть величину тисяч (39) і знайдіть між ними числа (27 і 64). Це означає, що перша цифра в відповідь 3, і відповідь в діапазоні 30.
2,2 км Кожна цифра від 0 до 9 з'являється в кубічних коренях чисел від 1 до 10 тільки один раз.
3. У З останньої цифри в нашому випадку 4, що означає, що остання цифра відповіді буде 4, так як в її кубічному корені остання цифра 4.
4. У Відповідь 34.
Русь 70
Щоб дізнатися, скільки років ви можете подвоювати гроші, розділіть номер 70 за річним процентним ставком.
Приклад:Скільки коштує подвійні гроші з річним процентним ставком на 17%?
70:17 = 4.1 років
Рулі 110
Щоб дізнатися, скільки років ви можете потроїти гроші, потрібно розділити число 110 на річний процентний ставок.
Приклад:Скільки років займає потрійні гроші на щорічній процентній ставці 20%?
110: 20 = 5.5 років
Магія No1089
І цей трюк здивує всіх! Подумайте про будь-який трицифровий номер, цифри якого в порядку зменшення, наприклад 642 або 864. Далі напишіть його в зворотному порядку і відніміть його з початкового числа. До отриманого числа додають той же номер, тільки письмовий в зворотному порядку. Що робити? 1089?
простий трюк.
Ви, ймовірно, бачили цей трюк багато: Подумайте про будь-який номер. Навколо його на 2. Додати 12. Розділіть його на 2. Відстежуйте оригінальний номер з нього.
Ви отримали 6, ви не отримали? Що б ви хочете, ви все ще отримаєте 6. І ось чому:
1,1 км 2,2 км
2. 2 + 12
3. (2 + 12): 2 = + 6
4. + 6 -
Це основні правила алгебри, і зараз ці хитрощі не здивують вас.
Не дивно, чому ми не навчаємо цього в школі. Виявляється, що багатозастосування стовпців застаріла, і ці секрети набагато корисніше, ніж більшість з яких ми навчалися в класах математики.
Покажіть ваші друзі, як зробити складні математичні розрахунки у вашому розумі!
через takprosto cc
10 Види людей, які порушують життя, починаючи з нового року без проблем!
10 найпопулярніших способів зв'язати шарф чоловіка, який зробить Ваш образ неповторним!